分治法:棋盘覆盖问题
在2k×2k的棋盘中有一个特殊方格,特殊方格的位置共有4k种情况。
下图是22×22棋盘的一种情况:

棋盘覆盖问题要求用下图中四种不同形态的L型骨牌覆盖这一个棋盘,并且L型骨牌之间不能重叠。

每个L型骨牌占三个格,抛去特殊方格,棋盘一共还剩4k-1个格,因此需要的方格数为(4k-1)/3个。
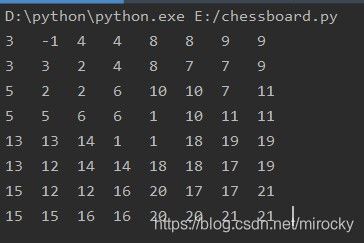
上例的棋盘经填充后变成下图:

使用分治策略,可以设计出一个简洁的算法:
将2k×2k的棋盘划分为2k-1×2k-1的四个小棋盘。特殊位置必落在其中一个棋盘中。将剩余三个棋盘靠中心的点记为新的特殊点,三个新的特殊点会构成一个L型骨牌。如下图所示:

然后再对2k-1的棋盘再次使用这个算法,只到棋盘只剩一个位置。
代码如下:
number = 0
def chess(board, top, bottom, left, right, x, y):
if bottom <= top or right <= left:
return
x_mid = top + (bottom - top) // 2
y_mid = left + (right - left) // 2
global number
number += 1
type = number
# 左上角
if x <= x_mid and y <= y_mid:
chess(board, top, x_mid, left, y_mid, x, y)
else:
board[x_mid][y_mid] = type
chess(board, top, x_mid, left, y_mid, x_mid, y_mid)
# 右上角
if x <= x_mid and y > y_mid:
chess(board, top, x_mid, y_mid + 1, right, x, y)
else:
board[x_mid][y_mid + 1] = type
chess(board, top, x_mid, y_mid + 1, right, x_mid, y_mid + 1)
# 左下角
if x > x_mid and y <= y_mid:
chess(board, x_mid + 1, bottom, left, y_mid, x, y)
else:
board[x_mid + 1][y_mid] = type
chess(board, x_mid + 1, bottom, left, y_mid, x_mid + 1, y_mid)
# 右下角
if x > x_mid and y > y_mid:
chess(board, x_mid + 1, bottom, y_mid + 1, right, x, y)
else:
board[x_mid + 1][y_mid + 1] = type
chess(board, x_mid + 1, bottom, y_mid + 1, right, x_mid + 1, y_mid + 1)
chessboard = [
[0, -1, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0],
]
chess(chessboard, 0, 7, 0, 7, 0, 1)
for i in range(0, 8):
for j in range(0, 8):
print(chessboard[i][j], end='\t')
print()
转载注明出处。