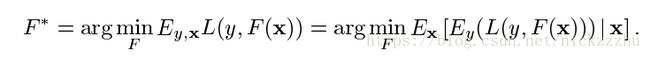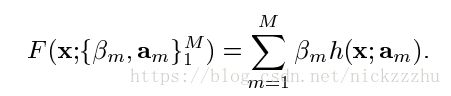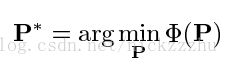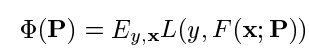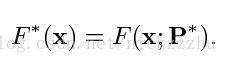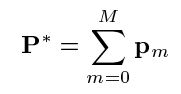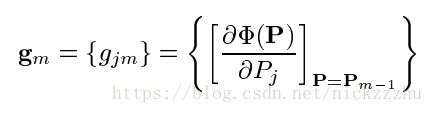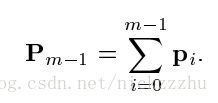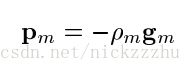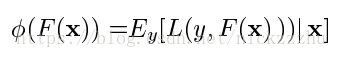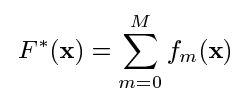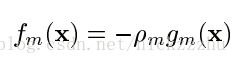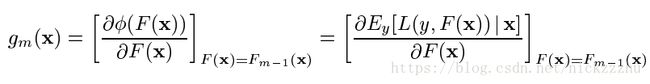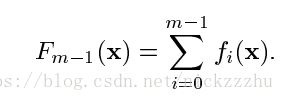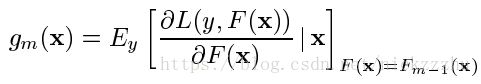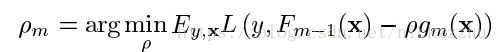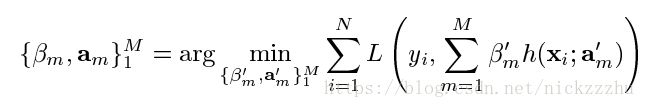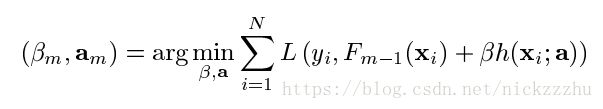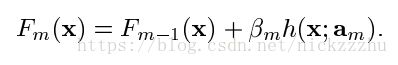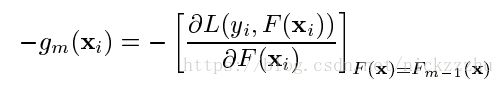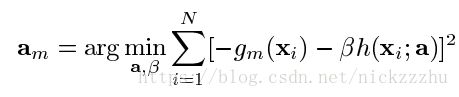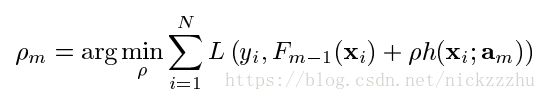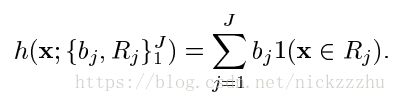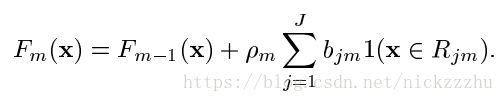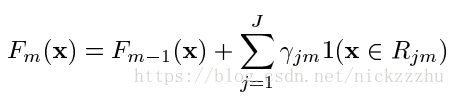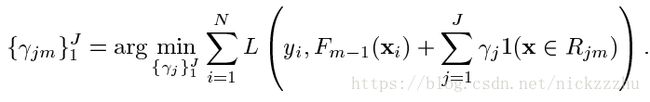GBDT原理解析：为什么说GBDT是拟合残差的梯度下降算法

写这篇博客是因为博主花了一天时间在网上找GBDT的原理解析，但发现所有介绍GBDT的文章都没有说清楚，尤其没有让博主明白为什么GBDT的每一步学习是基于之前的错误学习的，是在拟合残差。于是博主只好又花半天时间读了Friedman的原文的前半部分（后半部分开始介绍正则化、变量重要性定义和模拟实验了，没细看），感觉终于懂了80%-90%。博主觉得一定要把这个理解记下来，以便以后复习。

本博客主要参考论文Greedy Function Approximation: A Gradient Boosting Machine的1-4节，算是翻译+自己的理解。本文中还有部分图片来自这篇博客，该博客前面铺垫的知识讲得很好，但是对GBDT的原理推导却不够细

对机器学习基础的概念的介绍这里跳过，直接进入主题：GBDT是什么，为什么它是拟合残差的梯度下降算法

GBDT全名Gradient Boosting Decision Tree，从名字来看其实包含了三部分内容：

1）Gradient，代表了算法中的梯度下降思想

梯度下降是迭代优化的算法，其过程为

1，随机选择一个初始点w0

2，根据损失函数L和待优化参数w算出L相对于w在当前点的梯度d，梯度的负方向就是在当前点损失函数减小最多的方向

3，选择步长ρ

4，更新参数w=w+ρd

5，重复2-4步，直到满足停止条件。停止条件一般为梯度=0，或损失函数的减小成都小于一个阈值

2）Boosting，代表了算法中进行集成学习的思想

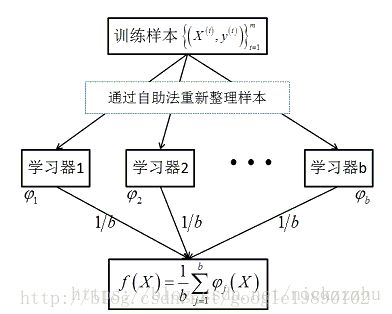
Boosting是用来提高弱分类器准确度的算法，其通过构造一系列弱分类器，以一定方式将他们组合成预测函数。Boosting和bagging是不同的。Bagging通过对样本多次采样（采样时样本可重复），并多次训练得到一系列学习器，最终通过平均的方法（如对于回归问题取平均，对于分类问题进行投票）得到学习结果。在bagging中，多个学习器之间是独立的，因此容易并行进行。Bagging的代表是随机森林，其示意图如下：

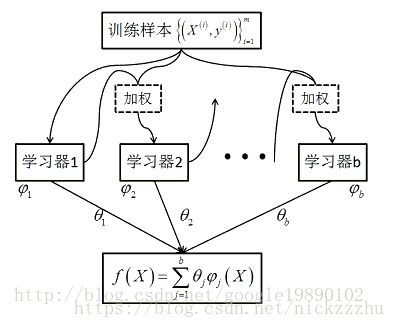
Boosting也生成一系列学习器，但生成过程是有依赖关系的。不同的boosting在生成过程中会对样本权重、学习器权重等有不同的处理，如XGBOOST,GBDT,ADABOOST在细节上不同。总的来说后一个学习器依赖前一个学习器的结果而生成，其示意图如下：

3，Decision Tree，代表了一类函数空间，Gradient和Boosting都是在Decision Tree上操作的。在GBDT中，最常用的决策树概念是CART，这是一种二叉回归树，它的损失函数是目标和预测值的欧氏距离

有监督学习、Gradient Decent、Boosting相结合：

以下最速下降、梯度下降、steepest-descent我是等价来用的，我理解梯度下降也是在局部点寻找函数下降最快的方向（就是梯度方向）并下降。论文原文中使用的是最速下降。

有监督学习就是要找到X到Y的映射F，使损失函数L最小。

一般来说，限制F是一个特定的函数模式，寻找参数P确定唯一的F。对于boosting方法，就是寻找以下形式

h是以a参数化的关于x的方程，不同的a确定了不同的单个h

对于参数化模型，寻找最佳方程的问题就变成寻找最佳参数P，使得损失函数最小。也就是：

其中损失函数为

根据以上条件得到的最佳近似函数为

对于大多数的F和L，使用数值方法求解，得到以下解的形式

其中p0是初始化值，pm是一系列连续的提升，可以认为是steps或boost，每一步都基于上一步。对于最速下降法，也就是梯度下降来说，求参数P的过程时首先定义pm的算法：

计算经过m-1步后的梯度

根据梯度计算pm值

其中gm是梯度方向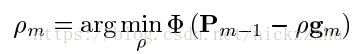，是使得损失函数在梯度方向下降最小的步长，可以使用线搜索方法得到。

对函数空间的优化

当应用以上数值优化方法到函数空间时，将整个函数F看成参数，因此对应了以下问题形式

损失函数为

F的形式为

F0是初始化值，fm是一系列提升。类似于参数的最速下降（梯度下降），在函数空间的最速下降是

其中下降的方向，即梯度是

经过m-1步得到的方程是

其中梯度g是期望的导数，可以变形为对不同数据点导数的期望：

同样的，最佳步长通过线搜索策略得到

有限数据集下的优化问题

以上函数空间的推导都是无参数化的，在有限数据中寻找（近似）最优解F需要对F进行参数化。例如将F用h进行参数化后，问题变为求解参数，使得损失函数最小

类似于gradient decent，使用greedy-stagewise的方法确定每一步m的最优参数

之后将h带入得到F

注意将stagewise和stepwise区分，stepwise每一步都更改之前的参数值，而stagewise每一步新加一个fm，但是之前确定的Fm-1不变

求解F还是一个对函数空间，将F看成参数的梯度下降过程。但是因为将F用h进行了参数化，所以F受到了限制，其每一步的更新必须在h的函数族内。而我们在第m步求梯度时得到的梯度方向公式为：

这是一个不依赖于hm，仅依赖于损失函数L，Fm-1和N个数据点（X,Y）的非参数化的式子。它表明了在每一步，基于已有数据的梯度方向。如果不考虑寻找最佳参数，沿着这个方向下降的损失函数较小最快。但现在参数化的h被限制了，而我们梯度下降时只能沿着hm下降，所以我们希望在hm尽可能地接近gm方向， 也就是hm尽可能让损失函数在m步最小化。当我们用欧式距离度量gm和hm时，寻找hm最佳参数的问题就变成

求得hm的参数后，用这个被限制了函数形式的hm代替gm，进行梯度下降更新。对于步长，同样是在梯度下降更新时使用线搜索：

得到步长和梯度方向后，更新映射F

在这里，gm是非参数化的，完全基于数据的最优梯度方向；计算hm和gm的欧氏距离，并寻找参数最小化之就是用hm去拟合gm，因此可以把gm看成pseudo-response。对于任意可导的损失函数L，使用steepest-descent求最佳函数F的算法：

1，初始化F0

2，设定M步循环，在每个循环m中

1. 计算损失函数L关于已有函数Fm-1得基于所有数据点的导数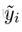，这就是第m步参数要拟合的pseudo-response，gm
2. 根据欧氏距离，将第m个函数fm=h和gm拟合，求距离最小化的参数am，这里可以得到类似梯度下降算法的梯度hm
3. 根据线搜索算法求最佳步长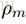，得到类似于梯度下降算法中的步长
4. 结合已有的Fm-1，用梯度和步长更新之

算法结束

此处终于可以解释GBDT在拟合残差是什么意思：每一步拟合pseudo-response而非拟合y，当损失函数L为RMSE时（即一般的回归的损失函数，也是CART的损失函数），gm就是对二次式求导，就是y-y_hat，也就是预测值和真实值的残差。所以说GBDT算法每一步优化都是在拟合残差。因此对于Least-Square Regression，算法如下：

引入决策树

当参数化函数h是树时，假设它有J个叶子节点，则h可以写成

（b，R）组成了h的参数。其中b是叶子节点的回归值，R是将点x映射到叶子节点的路径。F变成

R是到不同叶子节点的路径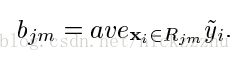，，是pseudo-response，用线搜索得到。F写成

其中

由于hm是树，所以一个hm可以看成是J个相互隔离的方程，所以寻找最优的hm就是寻找最优的，相互独立的方程

原本的优化问题变成了

所以问题就变成了根据Fm-1和损失函数L，更新树的每个叶子节点的常数值，是的m步的损失最小

在看论文原文的时候存在很多疑问，其中一个最大的疑问就是：是什么。这里我对比GBDT中函数更新公式和基础的梯度下降将其理解为更新梯度的步长，但是并不确定。梯度下降中步长是超参数，不是根据数据学习的，这里的是需要根据数据优化的。此外，在看XGBOOST原理时，线搜索是用在寻找最佳树结构上的，而这里是寻找最佳。如果是步长，该怎么用线搜索寻找最佳步长