LeetCode 1391. 检查网格中是否存在有效路径 (DFS+并查集)
文章目录
- 题目(图的静态连通性)
- 题解
-
- 最朴实的DFS做法
- 比较精简的写法
- 建图+FloodFill
- 并查集维护图的连通性
题目(图的静态连通性)
给你一个 m x n 的网格 grid。网格里的每个单元都代表一条街道。grid[i][j] 的街道可以是:
1 表示连接左单元格和右单元格的街道。
2 表示连接上单元格和下单元格的街道。
3 表示连接左单元格和下单元格的街道。
4 表示连接右单元格和下单元格的街道。
5 表示连接左单元格和上单元格的街道。
6 表示连接右单元格和上单元格的街道。
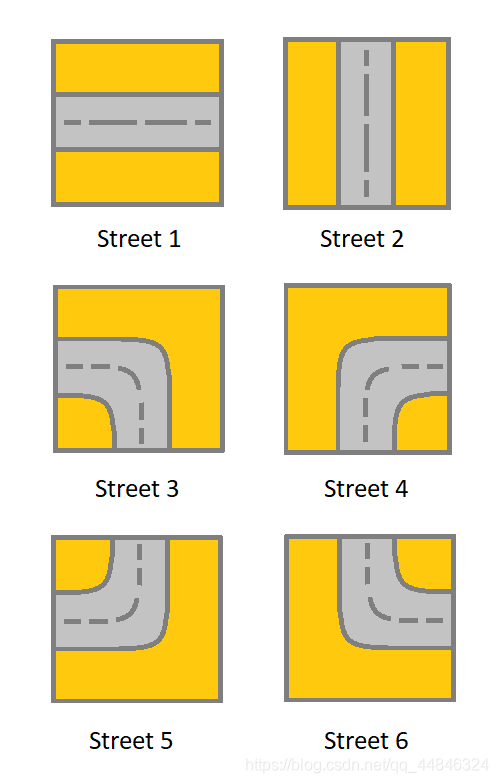
你最开始从左上角的单元格 (0,0) 开始出发,网格中的「有效路径」是指从左上方的单元格 (0,0) 开始、一直到右下方的 (m-1,n-1) 结束的路径。该路径必须只沿着街道走。
注意:你 不能 变更街道。
如果网格中存在有效的路径,则返回 true,否则返回 false 。
题解
最朴实的DFS做法
对于每一种不同的街道,它的转向是确定的,转完之后能够匹配的街道也是确定的,挨个枚举就好了。
注意防止左右往返的情况,所以一定要用一个visited[][]数组来记录一下,防止搜索冗余。
bool visited[310][310];
class Solution {
public:
int m,n;
vector<vector<int>> grid;
bool hasValidPath(vector<vector<int>>& grid) {
this->grid = grid;
memset(visited, 0, sizeof(visited));
m = (int)grid.size();
n = (int)grid[0].size();
visited[0][0] = true;
return dfs(0, 0);
}
bool dfs(int i,int j){
if(i==m-1 && j==n-1){
return true;
}
int node = grid[i][j];
switch (node) {
case 1:
{
int x = i,y = j-1;
if(inArea(x, y)&& toLeft(grid[x][y]) && !visited[x][y]){
visited[x][y] = true;
if(dfs(x, y)){
return true;}
visited[x][y] = false;
}
}
{
int x = i,y = j+1;
if(inArea(x, y)&& toRight(grid[x][y])&& !visited[x][y]){
visited[x][y] = true;
if(dfs(x, y)){
return true;}
visited[x][y] = false;
}
}
break;
case 2:
{
int x = i-1,y = j;
if(inArea(x, y)&& toUp(grid[x][y]) && !visited[x][y]){
visited[x][y] = true;
if(dfs(x, y)){
return true;}
visited[x][y] = false;
}
}
{
int x = i+1,y = j;
if(inArea(x, y)&& toDown(grid[x][y]) && !visited[x][y]){
visited[x][y] = true;
if(dfs(x, y)){
return true;}
visited[x][y] = false;
}
}
break;
case 3:
{
int x = i+1,y = j;
if(inArea(x, y)&& toDown(grid[x][y]) && !visited[x][y]){
visited[x][y] = true;
if(dfs(x, y)){
return true;}
visited[x][y] = false;
}
}
{
int x = i,y = j-1;
if(inArea(x, y)&& toLeft(grid[x][y]) && !visited[x][y]){
visited[x][y] = true;
if(dfs(x, y)){
return true;}
visited[x][y] = false;
}
}
break;
case 4:
{
int x = i+1,y = j;
if(inArea(x, y)&& toDown(grid[x][y]) && !visited[x][y]){
visited[x][y] = true;
if(dfs(x, y)){
return true;}
visited[x][y] = false;
}
}
{
int x = i,y = j+1;
if(inArea(x, y)&& toRight(grid[x][y]) && !visited[x][y]){
visited[x][y] = true;
if(dfs(x, y)){
return true;}
visited[x][y] = false;
}
}
break;
case 5:
{
int x = i,y = j-1;
if(inArea(x, y)&& toLeft(grid[x][y]) && !visited[x][y]){
visited[x][y] = true;
if(dfs(x, y)){
return true;}
visited[x][y] = false;
}
}
{
int x = i-1,y = j;
if(inArea(x, y)&& toUp(grid[x][y]) && !visited[x][y]){
visited[x][y] = true;
if(dfs(x, y)){
return true;}
visited[x][y] = false;
}
}
break;
case 6:
{
int x = i,y = j+1;
if(inArea(x, y)&& toRight(grid[x][y]) && !visited[x][y]){
visited[x][y] = true;
if(dfs(x, y)){
return true;}
visited[x][y] = false;
}
}
{
int x = i-1,y = j;
if(inArea(x, y)&& toUp(grid[x][y]) && !visited[x][y]){
visited[x][y] = true;
if(dfs(x, y)){
return true;}
visited[x][y] = false;
}
}
break;
default:
break;
}
return false;
}
bool inArea(int i,int j){
return i>=0 && i<m && j>=0 && j<n;
}
bool toLeft(int v){
return v==1 || v==4 || v==6;
}
bool toRight(int v){
return v==1 || v==3 || v==5;
}
bool toUp(int v){
return v==2 || v==3 || v==4;
}
bool toDown(int v){
return v==2 || v==5 || v==6;
}
};
比较精简的写法
(我自己写的太啰嗦了)
大概思想,方向数组按顺序写,比如上右下左,编号为0,1, 2, 3;每种街道的转向都是确定的,都只有两种,也用一个数组记录一下。
最后,根据每种街道类型的不同,依次选择两种方向,得出下一步,但是要判断是否可连接。
+2模4就相当于旋转180度,一种很实用的技巧。
(go[G[x][y]][i]+2)%4 ==go[G[nx][ny]][0] ||
(go[G[x][y]][i]+2)%4==go[G[nx][ny]][1]
// 上(0) 右(1) 下(2) 左(3)
const int dx[] = {
-1,0,1,0};
const int dy[] = {
0,1,0,-1};
//分别对应 6 种街道能转的2种方向,对应编号 0 1 2 3
const int go[][2] = {
{
},{
1,3},{
0,2},{
2,3},{
1,2},{
0,3},{
0,1}};
class Solution {
public:
int m,n;
vector<vector<int>> G;
bool visited[310][310] = {
0};
bool hasValidPath(vector<vector<int>>& grid) {
G = grid;
m = grid.size();
n = grid[0].size();
memset(visited,0,sizeof(visited));
return dfs(0,0);
}
bool dfs(int x,int y){
visited[x][y] = 1;
if(x==m-1&&y==n-1){
return true;
}
for(int i=0;i<2;i++){
int nx = x + dx[go[G[x][y]][i]];
int ny = y + dy[go[G[x][y]][i]];
if( nx>=0&&nx<m&&ny>=0&&ny<n&& !visited[nx][ny] &&
((go[G[x][y]][i]+2)%4 ==go[G[nx][ny]][0] || (go[G[x][y]][i]+2)%4==go[G[nx][ny]][1] ) ){
if(dfs(nx,ny)){
return true;}
visited[nx][ny] = 0;
}
}
return false;
}
};
建图+FloodFill
const int dx[] = {
-1,0,1,0};
const int dy[] = {
0,1,0,-1};
class Solution {
public:
int G[1000][1000],m,n;
vector<vector<int>> grid;
bool hasValidPath(vector<vector<int>>& grid) {
this->grid = grid;
m = grid.size();
n = grid[0].size();
memset(G,0,sizeof(G));
fill(G);
dfs(1,1);
return !G[3*m-2][3*n-2];
}
void dfs(int x,int y){
G[x][y] = 0;
for(int i=0;i<4;i++){
int nx = x + dx[i];
int ny = y + dy[i];
if(nx>=0&&ny>=0&&nx<3*m&&ny<3*n && G[nx][ny]){
dfs(nx,ny);
}
}
}
void fill( int(*G)[1000] ){
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
int v = grid[i][j];
G[3*i+1][3*j+1]=1;
if(v==1){
G[3*i+1][3*j]=G[3*i+1][3*j+2]=1;}
if(v==2){
G[3*i][3*j+1]=G[3*i+2][3*j+1]=1;}
if(v==3){
G[3*i+1][3*j]=G[3*i+2][3*j+1]=1;}
if(v==4){
G[3*i+2][3*j+1]=G[3*i+1][3*j+2]=1;}
if(v==5){
G[3*i+1][3*j]=G[3*i][3*j+1]=1;}
if(v==6){
G[3*i][3*j+1]=G[3*i+1][3*j+2]=1;}
}
}
}
};
并查集维护图的连通性
首先并查集维护连通性的时候,是通过merge(int x,int y)的方式,这就需要把图中的每一个网格点映射为一个唯一的整数。
这样做即可。
int getID(int x,int y){
return x*n+y;
}
那如何判断,某个street可以和另一个street合并呢?
可以仿照一开始的做法。
比如说,1号街道如果想和它左边的街道合并,左边的街道必须是(1 、3、5);如果1号街道想和它右边的街道合并,右边的街道只能是(1、4、6)。
其他街道一样处理。
最后要判断两个点的连通与否,只要看它们的代表元是否相同即可。
const int dx[] = {
-1,0,1,0};
const int dy[] = {
0,1,0,-1};
struct UnionFindSet{
int f[300*300+10];
UnionFindSet(){
for(int i=0;i<300*300;i++){
f[i] = i;
}
}
void merge(int x,int y){
f[find(x)] = find(y);
}
int find(int x){
return x==f[x]?x:f[x]=find(f[x]);
}
};
class Solution {
public:
vector<vector<int>> grid;
int m,n;
UnionFindSet ufs;
int getID(int x,int y){
return x*n+y;
}
bool inArea(int x,int y){
return x>=0&&x<m&&y>=0&&y<n;
}
void mergeL(int x,int y){
int nx = x,ny = y-1;
if(inArea(nx, ny)){
int v = grid[nx][ny];
if(v==1 || v==4 || v==6){
ufs.merge(getID(x, y), getID(nx, ny));
}
}
}
void mergeR(int x,int y){
int nx = x,ny = y+1;
if(inArea(nx, ny)){
int v = grid[nx][ny];
if(v==1 || v==3 || v==5){
ufs.merge(getID(x, y), getID(nx, ny));
}
}
}
void mergeU(int x,int y){
int nx = x-1,ny = y;
if(inArea(nx, ny)){
int v = grid[nx][ny];
if(v==2 || v==3 || v==4){
ufs.merge(getID(x, y), getID(nx, ny));
}
}
}
void mergeD(int x,int y){
int nx = x+1,ny = y;
if(inArea(nx, ny)){
int v = grid[nx][ny];
if(v==2 || v==5 || v==6){
ufs.merge(getID(x, y), getID(nx, ny));
}
}
}
bool hasValidPath(vector<vector<int>>& grid) {
this->grid = grid;
m = (int)grid.size();
n = (int)grid[0].size();
for(int x=0;x<m;x++){
for(int y=0;y<n;y++){
int kind = grid[x][y];
switch (kind) {
case 1:
mergeL(x, y);mergeR(x, y);
break;
case 2:
mergeU(x, y);mergeD(x, y);
break;
case 3:
mergeL(x, y);mergeD(x, y);
break;
case 4:
mergeR(x, y);mergeD(x, y);
break;
case 5:
mergeL(x, y);mergeU(x, y);
break;
case 6:
mergeR(x, y);mergeU(x, y);
break;
default:
break;
}
}
}
return ufs.find(getID(0, 0))==ufs.find(getID(m-1, n-1));
}
};
