数据结构 期中考试

全部每周作业和视频思考题答案和解析 见 浙江大学 数据结构 思考题+每周练习答案汇总

判断题：

答案：F T F T F   T F F T F

1-1 若一个结点是某二叉树的中序遍历序列的最后一个结点，则它必是该树的前序遍历序列中的最后一个结点。 (3分)

T         F

如果该树根只有左子树，则根节点为最后遍历到的节点，且是前序遍历的第一个节点。

1-2 一棵有124个结点的完全二叉树，其叶结点个数是确定的。 (3分)

T         F

 

1-3 用邻接表法存储图，占用的存储空间数只与图中结点个数有关，而与边数无关。 (3分)

T         F

 

1-4 算法分析的两个主要方面是时间复杂度和空间复杂度的分析。 (2分)

T         F

 

1-5 通过对堆栈S操作：Push(S,1), Push(S,2), Pop(S), Push(S,3), Pop(S), Pop(S)。输出的序列为：123。 (3分)

T         F

序列为2 3 1

1-6 如果无向图G必须进行两次广度优先搜索才能访问其所有顶点，则G一定有2个连通分量。 (3分)

T         F

 

1-7 在具有N个结点的单链表中，访问结点和增加结点的时间复杂度分别对应为O(1)和O(N)。 (3分)

T         F

都是O(N)

1-8 在用数组表示的循环队列中，front值一定小于等于rear值。 (2分)

T         F

 

1-9 若一棵平衡二叉树的所有非叶结点的平衡因子都是0，则其必为完美二叉树。(3分)

T         F

 

1-10 在一棵二叉搜索树上查找63，序列39、101、25、80、70、59、63是一种可能的查找时的结点值比较序列。 (3分)

T         F

第三个数25应该满足大于39这个条件，因为它前面的101是要大于39的。

选择题：

答案 ：B C B D A    B B C A A    A B

2-1 下列哪个函数是O(N)的？ (4分)

1. N(logN)​2​​
2. (logN)​2​​
3. (NlogN)/1000
4. N​2​​/1000

 

2-2 设h为不带头结点的单向链表。在h的头上插入一个新结点t的语句是：(4分)

1. h=t; t->next=h->next;
2. h=t; t->next=h;
3. t->next=h; h=t;
4. t->next=h->next; h=t;

 

2-3 先序遍历图示二叉树的结果为 (4分)

1. H，I，D，B，E，F，G，A，C
2. A，B，D，H，I，E，C，F，G
3. A，B，C，D，H，E，I，F，G
4. H，D，I，B，E，A，F，C，G

 

2-4 已知一棵完全二叉树的第6层（设根为第1层）有8个叶结点，则该完全二叉树的结点个数最多是： (4分)

1. 52
2. 119
3. 39
4. 111

因为 1+2+4+8+16+8 = 39 有些人可能会选 39 ，其实可能这8个叶节点是最后面的叶节点，即：

同样是第三层2个叶节点，但是它们的总节点数不一样多。

回到题目，第六层本来应该32个节点，有24个还有子树，故为 1 + 2 +4 +8+16+32+24*2  = 111

2-5 若某图的深度优先搜索序列是{V1, V4, V0, V3, V2}，则下列哪个图不可能对应该序列？ (4分)

1. 
2. 
3. 
4. 

 

2-6 循环顺序队列中是否可以插入下一个元素（）。 (4分)

1. 与曾经进行过多少次插入操作有关
2. 与队头指针和队尾指针的值有关
3. 只与数组大小有关，与队首指针和队尾指针的值无关
4. 只与队尾指针的值有关，与队头指针的值无关

 

2-7 对最小堆（小顶堆）{1,3,2,12,6,4,8,15,14,9,7,5,11,13,10} 进行三次删除最小元的操作后，结果序列为：(4分)

1. 4,5,6,12,7,10,8,15,14,13,9,11
2. 4,6,5,12,7,10,8,15,14,9,13,11
3. 4,5,6,7,8,9,10,11,12,13,14,15
4. 4,6,5,13,7,10,8,15,14,12,9,11

第一行：1 第二行：3 2 第三行：12 6   4 8 第四行：15 14 9 7   5 11 13 10

删除一次：第一行：2 第二行：3  4 第三行：12 6   5 8 第四行：15 14 9 7   10 11 13

删除二次：第一行：3 第二行：6  4 第三行：12  7   5 8 第四行：15 14 9 13   10 11

删除三次：第一行：4 第二行：6  5 第三行：12  7   10 8 第四行：15 14 9 13   11 

 

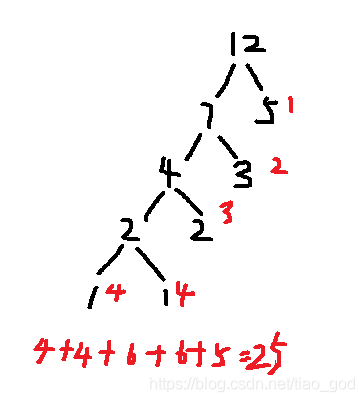
2-8 设一段文本中包含字符{a, b, c, d, e}，其出现频率相应为{3, 2, 5, 1, 1}。则经过哈夫曼编码后，文本所占字节数为： (4分)

1. 40
2. 12
3. 25
4. 36

 

2-9 表达式a*(b+c)-d的后缀表达式是： (4分)

1. a b c + * d -
2. a b c d * + -
3. - + * a b c d
4. a b c * + d -

 

2-10 三叉树中，度为1的结点有5个，度为2的结点3个，度为3的结点2个，问该树含有几个叶结点？ (4分)

1. 8
2. 13
3. 10
4. 12

n0 + n1 + n2 + n3 -1 = 总的边数

总的边数 = n0*0 + n1*1 + n2*2 + n3*3

n0 = n2 + 2*n3 +1 = 8

 

2-11 下列代码

for(i=0; i0; j/=2)
     printf(“%d\n”, j);

的时间复杂度是： (4分)

1. O(NlogN)
2. O(N)
3. O(N​2​​)
4. O(N×i)

 

2-12 在并查集问题中，已知集合元素0~8所以对应的父结点编号值分别是{ 1, -4, 1, 1, -3, 4, 4, 8, -2 }（注：−n表示树根且对应集合大小为n），那么将元素6和8所在的集合合并（要求必须将小集合并到大集合）后，该集合对应的树根和父结点编号值分别是多少？ (4分)

1. 1和-6
2. 4和-5
3. 8和-5
4. 8和-6

 

5-1 下列代码的功能是返回带头结点的单链表L的逆转链表。

List Reverse( List L )
{
    Position Old_head, New_head, Temp;
    New_head = NULL;
    Old_head = L->Next;

    while ( Old_head )  {
        Temp = Old_head->Next;
        (6分);  
        New_head = Old_head;  
        Old_head = Temp; 
    }
    (6分);
    return L;
}
Time Limit: 400 ms  Memory Limit: 64 MB

List Reverse( List L )
{
    Position Old_head, New_head, Temp;
    New_head = NULL;
    Old_head = L->Next;

    while ( Old_head )  {
        Temp = Old_head->Next;
        Old_head->Next = New_head;
        New_head = Old_head;  
        Old_head = Temp; 
    }
    L->Next = New_head;
    return L;
}

5-2 下列代码的功能是将大顶堆H中指定位置P上的元素的整数键值上调D个单位，然后继续将H调整为大顶堆。

void IncreaseKey( int P, int D, PriorityQueue H )
{
   int i, key;
   key = H->Elements[P] + D;
   for ( i = (6分); H->Elements[i/2] < key; i/=2 )
      (6分);
   H->Elements[i] = key;
}

void IncreaseKey( int P, int D, PriorityQueue H )
{
   int i, key;
   key = H->Elements[P] + D;
   for ( i = P; H->Elements[i/2] < key; i/=2 )
      H->Elements[i] = H->Elements[i/2];
   H->Elements[i] = key;
}