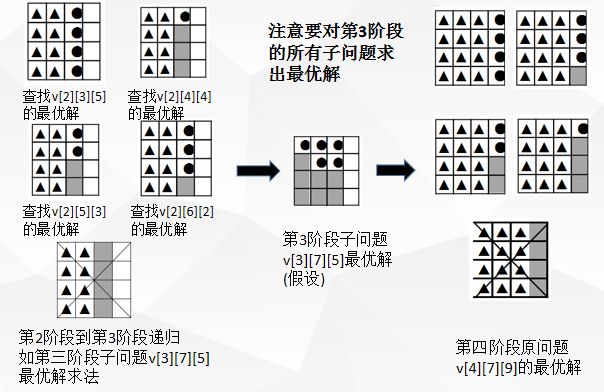
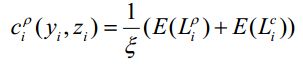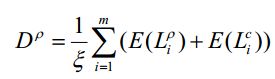动态规划求解库位分配问题
layout: post
title: 基于动态规划的库位分配算法
subtitle: 使用拣货路径长度优化人到货拣货的仓库库位分配
date: 2020-01-15
author: ZS
header-img: img/post-bg-ios9-web.jpg
catalog: true
tags:
- Dynamic Program
- Algorithm
- Schedule
使用拣货路径长度优化人到货拣货的仓库库位分配
各位读者大家好,今天ZS给大家分享使用动态规划算法求解库位分配问题。算法的主要思想来自于论文:Exact route-length formulas and a storage location assignment heuristic for picker-to-parts warehouses。动态规划算法一直以来都是让人很摸不到头脑的算法,小编刚开始写这个程序的时候,真是写到崩溃,但是要始终相信社会主义核心价值观,只要思想不滑坡,就可以捋顺思路!言归正传,上!
动态规划算法典型算例
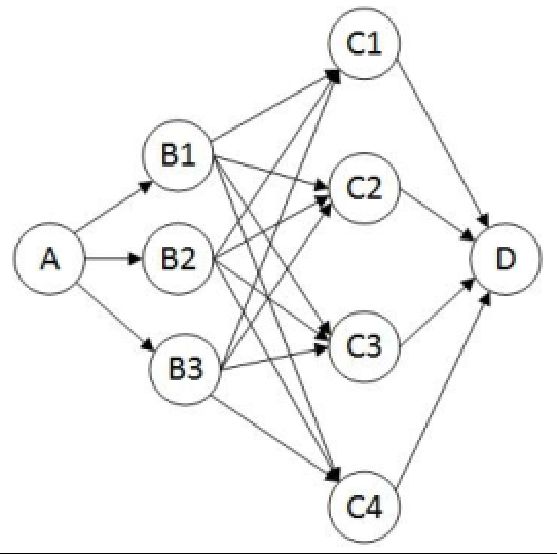
动态规划算法的核心思想是通过子问题的最优解求解出原问题的最优解。图1 所示,求从A到D的最短路径,如果已知从A到C1的最短路径Pac1,从A到C2的最短路径Pac2,从A到C3的最短路径Pac3,从A到C4的最短路径Pac4。那么从A到D的最短路径是 min{Pac1+C1D,Pac2+C2D,Pac3+C3D,Pac4+C4D}
这样逐步向前推进,就可以算得最短路径。
库位分配问题简介
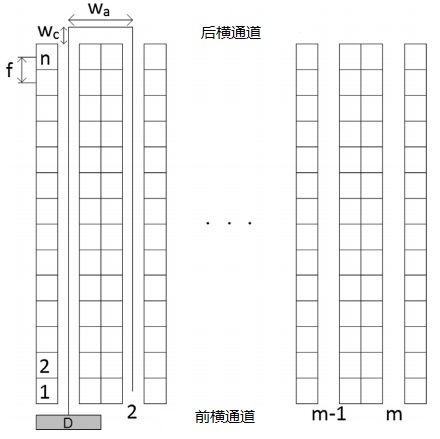
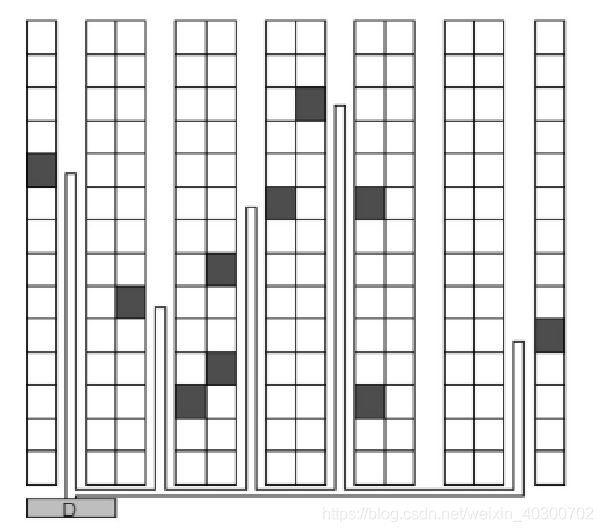
如图2所示,纵向通道两边是货架,用于存货。前后两个横通道连接各货架。纵向通道货架左右对称,入库出库无差别,认为两者属于同一列。
简化处理
-
按需求频率由大到小将货物分为A,B,C三类。(需求频率:给定订单,需要各类货物的占比) -
货物数目和库位数目相等。各类货物总数一定。
目的
- 每一个库位匹配合理的货物类型
概率假设
- 给定拣货订单,拣选每个A的概率都相等,B,C同理。

- 每个货物都有一定概率被拣选,将货物分配到库位中,也就确定了在某处拣货的概率。pij是本算法中比较关键的变量。
- 货物在仓库中的分布优化问题 ------>>>> 仓库中的拣货概率分布问题
评价指标-平均拣货路径长度
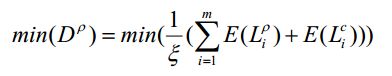
图4以图3中的拣货路径策略为例,求解给定一概率分布下,平均拣货路径长度,以此作为目标函数,优化仓库中货物的类别分布。
动态规划求解库位分配问题
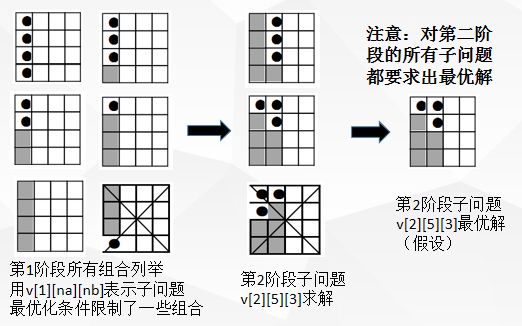
以4×4格局仓库,A,B两种货物说明动态规划算法:
用v[m][na][nb]表示子问题,将货物na,nb分配到前m通道。
/*
动态规划算法的伪代码
*/
for i←0 to all
for j←0 to all-i
k←all-i-j
if i,j,k 不符合约束条件
then continue
culum cu(i,j,k)
cu.Sofar_length←某较大的数
for o←0 to all_last
for p←0 to all_last-o
q←all_last-o-p
if o,p,q 不符合约束条件
then continue
计算 zi
culum cu(zi)
cu.计算转化成本
if 转换成本+v[m-1][o][p]代码实现
/************************动态规划算法的核心*************************************************************/
void calcul::doDP(vector *ans)
{
culum ***v;
v=new culum **[M];
for(int m=0;mlastI||(ma+mb)>(lastI+lastJ)) //最优化条件,条件要搞清楚
continue;
cu_temp=v[0][ma][mb]; //单个通道的库位分配 只有库位分配 ELi enterprob有价值
cu_temp.calcul_cost(m+1,i,j,k); //计算lastprob,Elc,以及cost
if(v[m-1][o][p].Sofar_length+cu_temp.get_cost()lastI||(ma+mb)>(lastI+lastJ)) //最优化条件
continue;
cu_temp=v[0][ma][mb];
cu_temp.calcul_cost(m+1,i,j,k);
if(v[m-1][o][p].Sofar_length+cu_temp.get_cost() 实验结果
在图7 中每一行代表仓库的一条通道。第1列是通道编号,第2、3、4列是各类货物的数目,最后一列是评价值。
参考文献
[1]Arjan S. Dijkstra,Kees Jan Roodbergen. Exact route-length formulas and a storage location assignment heuristic for picker-to-parts warehouses[J]. Transportation Research Part E,2017,102.
[2] 源代码地址:https://github.com/zs997/warehouse