信号与系统 (施工中)
请按照右侧目录浏览
傅里叶分析之掐死教程(完整版)更新于2014.06.06
1.1序言
- 消息
语言文字、声音、图像、统计数据等 - 信息
人们需要的消息称为信息 - 信号
信号是携带消息的随时间变化的物理量
用f(t)表示激励信号,y(t)表示响应信号 - 系统
相互制约又相互作用的个体所组成的具有一定功能的整体
1.2信号的描述及分类
分类
用一个单变量或多变量的函数来表示
自变量
- 时间
- 空间
- 频率
- ……
以时间t为自变量,信号可以表示为t的函数,用函数f(t),y(t)表征
时间特性
- 信号在某一时刻的大小
- 信号持续时间的长短
- 信号变化的快慢
- ……
这些都可以从波形图上反映出来,信号的这一特性叫做信号的时间特性
频率特性
信号在一定条件下又可分解为不同频率的正弦分量之和,正弦分量的振幅和初相位与频率之间的关系叫做信号的频率特性
描述
确定和随机
- 对于每一时刻
t都有确定的函数值与其对应,这样的信号称为确定信号 - 随机信号不能写出确定的时间函数表达式,只能用概率统计的方法来描述
连续和离散
- 除了有限个间断点以外,如果一个信号在任意时刻均有定义值,则称其为连续信号
- 只在一系列离散的瞬间有确切定义而在其他时刻无定义的信号叫做离散时间信号,简称离散信号
时限
时限信号
时间域有始有终的信号,信号出现在[t1, t2]
f ( t ) = { f ( t ) , t 1 ≤ t ≤ t 2 0 , t < t 1 , t > t 2 f(t) = \begin{cases} f(t),&t_1 \le t \le t_2\\ 0,& t \lt t_1,t \gt t_2 \end{cases} f(t)={ f(t),0,t1≤t≤t2t<t1,t>t2
有终信号
时间域无始有终的信号,(-∞, t0]
f ( t ) = { f ( t ) , t ≤ t 0 0 , t > t 0 f(t) = \begin{cases} f(t),&t \le t_0\\ 0,& t \gt t_0 \end{cases} f(t)={ f(t),0,t≤t0t>t0
有始信号
时间域有始无终的信号,[t0, +∞)
f ( t ) = { f ( t ) , t ≥ t 0 0 , t < t 0 f(t) = \begin{cases} f(t),&t \ge t_0\\ 0,& t \lt t_0 \end{cases} f(t)={ f(t),0,t≥t0t<t0
因果信号
有始信号在t = 0时刻起始,[0, +∞)
f ( t ) = { f ( t ) , t ≥ 0 0 , t < 0 f(t) = \begin{cases} f(t),&t \ge 0\\ 0,& t \lt 0 \end{cases} f(t)={ f(t),0,t≥0t<0
反因果信号
起始信号的反转,,(-∞, 0]
f ( t ) = { f ( t ) , t ≤ 0 0 , t > 0 f(t) = \begin{cases} f(t),&t \le 0\\ 0,& t \gt 0 \end{cases} f(t)={ f(t),0,t≤0t>0
无时限信号
时间域无始无终的信号
f ( t ) = f ( t ) ( − ∞ < t < ∞ ) f(t) = f(t) (-\infin \lt t \lt \infin) f(t)=f(t)(−∞<t<∞)
周期
周期信号的特点
- 具有周期
- 定义域无始无终
非周期信号不具备这两个特点
两个及两个以上的周期信号的叠加可能是周期信号,也可能是非周期信号,其中能找到最小公倍周期的为周期信号,否则就是非周期信号。
连续周期信号
f T ( t ) = f ( t − k T ) , k = 0 , ± 1 , ± 2 , . . . , T > 0 f_T(t) = f(t-kT), k=0, \pm1,\pm2,..., T\gt 0 fT(t)=f(t−kT),k=0,±1,±2,...,T>0
离散周期信号
f N ( k ) = f ( k − m N ) , m = 0 , ± 1 , ± 2 , . . . , N > 0 f_N(k) = f(k-mN), m=0, \pm1,\pm2,..., N\gt 0 fN(k)=f(k−mN),m=0,±1,±2,...,N>0
能量与功率
1Ω的电阻上消耗的瞬时功率为
p ( t ) = u 2 ( t ) p ( t ) = i 2 ( t ) p(t) = u^2(t) \\ p(t) = i^2(t) p(t)=u2(t)p(t)=i2(t)
将电压和电流抽象为一般意义的信号
p ( t ) = f 2 ( t ) p(t) = f^2(t) p(t)=f2(t)
时间区间[-τ,τ]
区间归一化能量
E = ∫ − τ τ p ( t ) d t = ∫ − τ τ ∣ f ( t ) ∣ 2 d t E = \int^\tau_{-\tau}p(t)dt = \int^\tau_{-\tau}|f(t)|^2dt E=∫−ττp(t)dt=∫−ττ∣f(t)∣2dt
归一化平均功率
P = 1 2 τ ∫ − τ τ ∣ f ( t ) ∣ 2 d t P = \frac 1 {2\tau} \int^\tau_{-\tau}|f(t)|^2dt P=2τ1∫−ττ∣f(t)∣2dt
全时域(-∞,∞)
归一化总能量
E 总 = lim τ → ∞ ∫ − τ τ ∣ f ( t ) ∣ 2 d t E_总 = \lim_{\tau \rightarrow \infin}\int^\tau_{-\tau}|f(t)|^2dt E总=τ→∞lim∫−ττ∣f(t)∣2dt
归一化平均功率
P = lim τ → ∞ 1 2 τ ∫ − τ τ ∣ f ( t ) ∣ 2 d t P = \lim_{\tau \rightarrow \infin} \frac 1 {2\tau} \int^\tau_{-\tau}|f(t)|^2dt P=τ→∞lim2τ1∫−ττ∣f(t)∣2dt
分类
| 总能量 | 平均功率 | |
|---|---|---|
| 功率信号 | ∞ | 有限 |
| 能量信号 | 有限 | ∞ |
| 非功非能信号 | ∞ | ∞ |
不存在功率有界能量也有界的信号
离散信号
离散信号f(k)的归一化总能量
E 总 = lim n → ∞ ∑ k = − n n ∣ f ( k ) ∣ 2 ( − n ≤ k ≤ n ) E_总 = \lim_{n \rightarrow \infin} \displaystyle\sum_{k=-n}^n|f(k)|^2(-n \le k \le n ) E总=n→∞limk=−n∑n∣f(k)∣2(−n≤k≤n)
归一化平均功率
P = lim n → ∞ 1 2 n + 1 ∑ k = − n n ∣ f ( k ) ∣ 2 ( − n ≤ k ≤ n ) P = \lim_{n \rightarrow \infin} \frac 1 {2n+1}\displaystyle\sum_{k=-n}^n|f(k)|^2(-n \le k \le n ) P=n→∞lim2n+11k=−n∑n∣f(k)∣2(−n≤k≤n)
2n + 1的1指的是t = 0时刻的信号
信号分类
| 功率信号 |
|---|
| 连续的周期信号 |
| 直流信号 |
| 单位阶跃信号 |
| 能量信号 |
|---|
| 时限脉冲信号 |
| 单边指数衰减信号 |
| 非功非能信号 |
|---|
| 指数增长信号 |
1.3典型信号
典型连续信号
复指数信号
f ( t ) = A e s t s = σ + j ω σ 、 ω 为 实 数 f(t)=Ae^{st}\\ s = \sigma + j\omega\\ \sigma、\omega为实数 f(t)=Aests=σ+jωσ、ω为实数
s称为复频率
A e s t = A e ( σ + j ω ) t = A e σ t e j ω t \begin{aligned} Ae^{st} &= Ae^{(\sigma+j\omega)t}\\ &= Ae^{\sigma t}e^{j\omega t} \end{aligned} Aest=Ae(σ+jω)t=Aeσtejωt
欧拉公式
e i x = c o s x + i s i n x e^{ix} = cosx+isinx eix=cosx+isinx
A e σ t e j ω t = A e σ t ( c o s ω t + j s i n ω t ) Ae^{\sigma t}e^{j\omega t} = Ae^{\sigma t}(cos\omega t+jsin\omega t) Aeσtejωt=Aeσt(cosωt+jsinωt)
- 当ω = 0时,
f(t)为实指数信号 - 当σ = 0时,
f(t)为虚指数信号,实部和虚部是正弦信号
实指数信号
f ( t ) = A e σ t f(t) = Ae^{\sigma t} f(t)=Aeσt
- σ > 0,
f(t)为指数增长信号 - σ < 0,
f(t)为指数衰减信号 - σ = 0,
f(t)为直流信号
通常把|σ|的倒数称为指数信号的时间常数
τ = 1 ∣ σ ∣ \tau = \frac 1 {|\sigma|} τ=∣σ∣1
τ越大指数信号增长或衰减越慢
单边衰减指数信号
f ( t ) = { 0 , t < 0 A e − t τ , t ≥ 0 f(t) = \begin{cases} 0,&t \lt 0\\ Ae^{- \frac t \tau},& t \ge 0 \end{cases} f(t)={ 0,Ae−τt,t<0t≥0
实指数信号对时间的微分和积分仍然是实指数信号
正弦信号
f ( t ) = A c o s ( ω t + φ ) f(t) = Acos(\omega t + \varphi ) f(t)=Acos(ωt+φ)
正弦信号的平均功率
P = A 2 2 P = \frac {A^2} 2 P=2A2
两个频率不同的正弦信号叠加,满足一定条件才是周期信号
f ( t ) = c o s ω 1 t + c o s ω 2 t f(t) = cos\omega_1t + cos\omega_2t\\ f(t)=cosω1t+cosω2t
ω 1 ω 2 = T 1 T 2 = m n \frac {\omega_1} {\omega_2} = \frac {T_1} {T_2} = \frac m n ω2ω1=T2T1=nm
m/n是最简分式,则f(t)是周期信号,其周期为最小公倍周期
T = m T 1 = n T 2 T = mT_1 = nT_2 T=mT1=nT2
变幅正弦振荡信号
f ( t ) = A e σ t c o s ω t f(t) = Ae^{\sigma t} cos\omega t f(t)=Aeσtcosωt
复指数信号
A e σ t c o s ω t + ( A e σ t s i n ω t ) j Ae^{\sigma t}cos\omega t+(Ae^{\sigma t}sin\omega t)j Aeσtcosωt+(Aeσtsinωt)j
它的实部和虚部是变幅正弦振荡信号
f r ( t ) = R e [ A e s t ] = A e σ t c o s ω f_r(t) = Re[Ae^{st}] = Ae^{\sigma t}cos\omega fr(t)=Re[Aest]=Aeσtcosω
f i ( t ) = I m [ A e s t ] = A e σ t s i n ω t f_i(t) = Im[Ae^{st}] = Ae^{\sigma t}sin\omega t fi(t)=Im[Aest]=Aeσtsinωt
- σ < 0,振幅按指数规律衰减
- σ > 0,振幅按指数规律增长
抽样(Sample)信号
f ( t ) = s i n t t = S a ( t ) f(t) = \frac {sint} t = Sa(t) f(t)=tsint=Sa(t)

- f ( t ) = 0 , t = n π ( n ∈ Z ) f(t) = 0, t = n\pi( n \in Z) f(t)=0,t=nπ(n∈Z)
- lim t → 0 S a ( t ) = 1 \lim_{t\rightarrow0}Sa(t) = 1 t→0limSa(t)=1
- ∫ 0 ∞ S a ( t ) d t = π 2 , ∫ − ∞ ∞ S a ( t ) d t = π \int^\infin_0Sa(t)dt = \frac \pi 2, \int^\infin_{-\infin}Sa(t)dt = \pi ∫0∞Sa(t)dt=2π,∫−∞∞Sa(t)dt=π
高斯脉冲信号
f ( t ) = A e − ( t τ ) 2 f(t) = Ae^{ {-(\frac t \tau)}^2} f(t)=Ae−(τt)2
奇异函数
单位斜坡(Ramp)信号
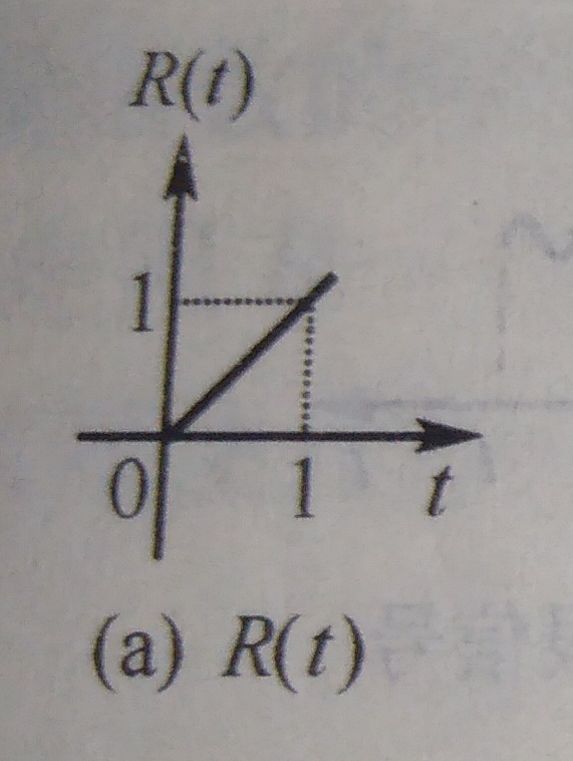
R ( t ) = t ε ( t ) = { 0 , t < 0 t , t ≥ 0 R(t) = t\varepsilon(t) =\begin{cases} 0,&t \lt 0\\ t,& t \ge 0 \end{cases} R(t)=tε(t)={ 0,t,t<0t≥0
有延迟的单位斜变信号
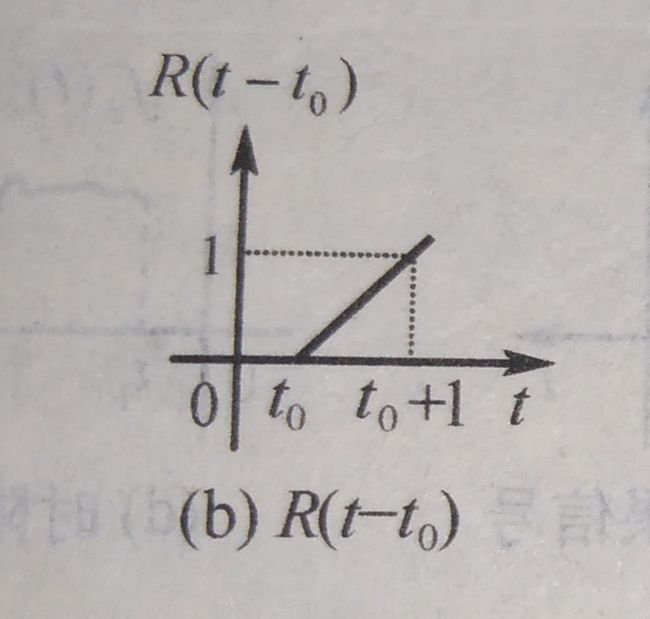
R ( t − t 0 ) = ( t − t 0 ) ε ( t − t 0 ) { 0 , t < t 0 t − t 0 , t ≥ t 0 R(t-t_0) = (t-t_0)\varepsilon(t-t_0) \begin{cases} 0,&t \lt t_0\\ t-t_0,& t \ge t_0 \end{cases} R(t−t0)=(t−t0)ε(t−t0){ 0,t−t0,t<t0t≥t0
截平斜变信号

f 1 ( t ) = R 1 ( t ) = { A τ R ( t ) , t < τ A , t ≥ τ f_1(t) = R_1(t) = \begin{cases} \frac A \tau R(t),&t \lt \tau\\ A,& t \ge \tau \end{cases} f1(t)=R1(t)={ τAR(t),A,t<τt≥τ
锯齿形脉冲信号

f 1 ( t ) = R 2 ( t ) = { A τ R ( t ) , t ≤ τ 0 , t > τ f_1(t) = R_2(t) = \begin{cases} \frac A \tau R(t),&t \le \tau\\ 0,& t \gt \tau \end{cases} f1(t)=R2(t)={ τAR(t),0,t≤τt>τ
正三角Δ 脉冲信号
f 3 ( t ) = A Δ 2 τ ( t ) = R 1 ( t + τ ) − R 1 ( t ) = { A ( 1 − ∣ t ∣ τ ) , ∣ t ∣ ≤ τ 0 , ∣ t ∣ > τ f_3(t) = A\Delta_{2\tau}(t) = R_1( t + \tau ) - R_1(t) = \begin{cases} A( 1 - \frac {|t|} \tau ),&|t| \le \tau\\ 0,& |t| \gt \tau \end{cases} f3(t)=AΔ2τ(t)=R1(t+τ)−R1(t)={ A(1−τ∣t∣),0,∣t∣≤τ∣t∣>τ
单位阶跃信号 ε

ε ( t ) = { 1 , t > 0 0 , t < 0 \varepsilon(t) = \begin{cases} 1,&t \gt 0\\ 0,& t \lt 0 \end{cases} ε(t)={ 1,0,t>0t<0
有延迟的单位阶跃信号
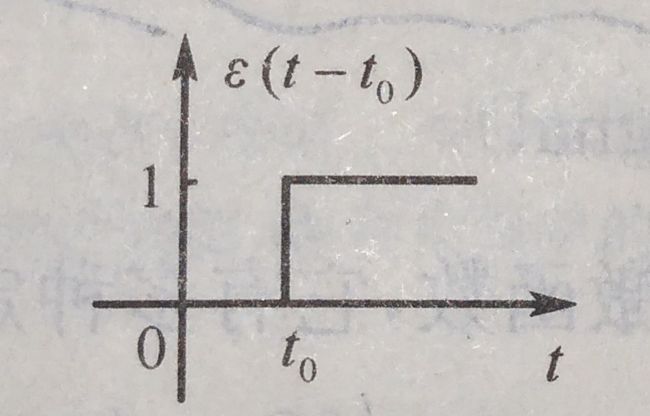
ε ( t − t 0 ) = { 1 , t > t 0 0 , t < t 0 \varepsilon(t-t_0) = \begin{cases} 1,&t \gt t_0\\ 0,& t \lt t_0 \end{cases} ε(t−t0)={ 1,0,t>t0t<t0
单位门(Gate)函数

g τ ( t ) = ε ( t + τ 2 ) − ε ( t − τ 2 ) g_\tau(t) = \varepsilon(t+\frac \tau 2) - \varepsilon(t-\frac \tau 2) gτ(t)=ε(t+2τ)−ε(t−2τ)
单位阶跃信号用来表示信号的非零值时间定义域
- 在t > 0有定义的因果信号可表示为
f 1 ( t ) = f ( t ) ε ( t ) f_1(t) = f(t)\varepsilon(t) f1(t)=f(t)ε(t) - 在t < 0有定义的反因果信号
f 2 ( t ) = f ( t ) ε ( − t ) f_2(t) = f(t)\varepsilon(-t) f2(t)=f(t)ε(−t) - 在t1 < t < t2有定义的时限信号
f 3 ( t ) = f ( t ) [ ε ( t − t 1 ) − ε ( t − t 2 ) ] f_3(t) = f(t)[\varepsilon(t-t_1) - \varepsilon(t-t_2)] f3(t)=f(t)[ε(t−t1)−ε(t−t2)]
一个函数乘以门函数,只留下门函数内的部分
符号(Sgn)函数
s g n ( t ) = { 1 , t > 0 − 1 , t < 0 sgn(t) = \begin{cases} 1,&t \gt 0\\ -1,& t \lt 0 \end{cases} sgn(t)={ 1,−1,t>0t<0
s g n ( t ) = 2 ε ( t ) − 1 = ε ( t ) − ε ( − t ) sgn(t) = 2\varepsilon(t) - 1 = \varepsilon(t) - \varepsilon(-t) sgn(t)=2ε(t)−1=ε(t)−ε(−t)
ε(t)和R(t)的关系
- ε(t)是R(t)的导数
- R(t)是ε(t)的积分
R ( t ) = ∫ − ∞ t ε ( τ ) d τ = ∫ 0 − t ε ( τ ) d τ R(t) = \int^t_{-\infin}\varepsilon(\tau)d\tau = \int^t_{0_-}\varepsilon(\tau)d\tau R(t)=∫−∞tε(τ)dτ=∫0−tε(τ)dτ
ε ( t ) = d R ( t ) d t \varepsilon(t) = \frac {dR(t)} {dt} ε(t)=dtdR(t)
单位冲激信号 δ
δ ( t ) = { ∞ , t = 0 0 , t ≠ 0 \delta(t) = \begin{cases} \infin,&t = 0\\ 0,& t \ne 0 \end{cases} δ(t)={ ∞,0,t=0t=0
单位冲激函数的强度
∫ ∞ ∞ δ ( t ) d t = 1 \int^\infin_\infin \delta(t)dt = 1 ∫∞∞δ(t)dt=1
加权性质
若函数f(t)在t = 0时连续
f ( t ) δ ( t ) = f ( 0 ) δ ( t ) f(t)\delta(t) = f(0)\delta(t) f(t)δ(t)=f(0)δ(t)
取样性质
若函数f(t)在t = 0时连续
∫ − ∞ ∞ f ( t ) δ ( t ) d t = f ( 0 ) \int^\infin_{-\infin}f(t)\delta(t)dt = f(0) ∫−∞∞f(t)δ(t)dt=f(0)
推论
若函数f(t)在t = t0时连续
f ( t ) δ ( t − t 0 ) = f ( t 0 ) δ ( t − t 0 ) f(t)\delta(t-t_0) = f(t_0)\delta(t-t_0) f(t)δ(t−t0)=f(t0)δ(t−t0)
∫ − ∞ ∞ f ( t ) δ ( t − t 0 ) d t = f ( t 0 ) \int^\infin_{-\infin}f(t)\delta(t-t_0)dt = f(t_0) ∫−∞∞f(t)δ(t−t0)dt=f(t0)