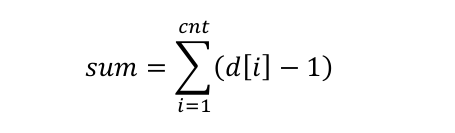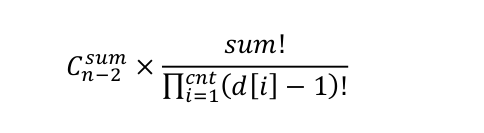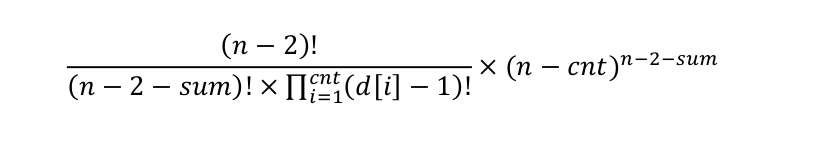从这星期起,我开始了怒刷BZOJ的旅程。这几天刷了10道题(由于“档期”的原因,所以有几道题没打完…..捂脸……..)
精简题解:
1000 A+B Problem
……..
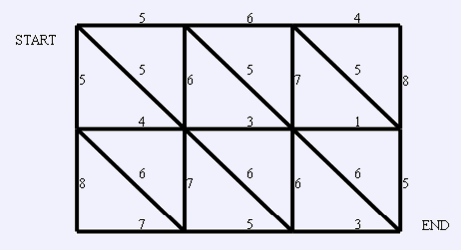
[BeiJing2006]狼抓兔子
裸的网络流,不过data有点大。。。。。。
哈,这图的性质太好了,就是一个平面图额,并且也很容易转化成对偶图,So……spfa怒跑之……
[FJOI2007]轮状病毒
Matrix-tree定理
不过,这道题有个线性递推式:f[n] = 3 * f[n - 1] – f[I - 2] + 2
线性递推推导过程参考这:http://vfleaking.blog.163.com/blog/static/17480763420119685112649/
Python大法好:
/**************************************************************
Problem: 1002
User: vivym
Language: Python
Result: Accepted
Time:88 ms
Memory:6360 kb
****************************************************************/
a = [0 for x in range(0,105)]
n = input()
a[1] = 1; a[2] = 5;
if n <= 2:
print a[n]
else:
for i in range(3,n + 1): a[i] = 3 * a[i - 1] - a[i - 2] + 2
print a[n]
上个没打高精的代码:
/**************************************************************
Problem: 1002
User: vivym
Language: C++
Result: Wrong_Answer
****************************************************************/
#include
#include
#include
#include
using namespace std;
const double eps = 1e-8;
const int maxn = 100 + 10;
typedef double Matrix[maxn][maxn];
void gauss_jordan(Matrix A,int n)
{
register int i,j,k,r;
for(i = 0;i < n;i ++)
{
r = i;
for(j = i + 1;j < n;j ++)
if(fabs(A[j][i]) > fabs(A[r][i])) r = j;
if(fabs(A[r][i]) < eps) continue;
if(r != i) for(j = 0;j <= n;j ++) swap(A[r][i],A[i][j]);
for(k = 0;k < n;k ++) if(k != i)
for(j = n;j >= i;j --) A[k][j] -= A[k][i] / A[i][i] * A[i][j];
}
}
Matrix mat;
int main()
{
int n;
scanf("%d",&n);
for(int i = 0;i < n;i ++)
{
mat[i][(i + 1) % n] = -1;
if(!i) mat[i][n - 1] = -1;
else mat[i][i - 1] = -1;
}
for(int i = 0;i < n;i ++) mat[i][i] = 3;
gauss_jordan(mat,n);
double ans = 1;
for(int i = 0;i < n;i ++) ans *= mat[i][i];
printf("%lld",(long long)ans);
return 0;
}
[ZJOI2006]物流运输trans:
Dp + 最短路
一开始看错题了。。。。。。啊啊啊。。。
f[i] = min(f[j] + K + (i – j) * spfa())
最后答案要减K。。。。因为从0转移是不需要加K的。
[HNOI2008]Cards:
裸的Burnside引理。并且置换群直接就给出了,省了我们自己DFS了。
求不动方案时用dp(k背包)搞。。。(一个循环节只能染一种颜色,So….你懂的)
/**************************************************************
Problem: 1004
User: vivym
Language: C++
Result: Accepted
Time:748 ms
Memory:5328 kb
****************************************************************/
#include
#include
using namespace std;
int f[105][105][105];
int g[105],vis[105],loop[105],id[105],sum[105],cnt;
int mod;
inline int pow(int a,int b)
{
int ret = 1;
for(; b ; b >>= 1,a = (a * a) % mod)
if(b & 1) ret = (ret * a) % mod;
return ret;
}
int main()
{
int sr,sb,sg,m,n,ans = 0;
scanf("%d%d%d%d%d",&sr,&sb,&sg,&m,&mod);
n = sr + sb + sg;
for(int i = 0;i <= m;i ++)
{
if(i == m) for(int j = 1;j <= n;j ++) g[j] = j;
else for(int j = 1;j <= n;j ++) scanf("%d",g + j);
memset(f,0,sizeof(f)); memset(vis,0,sizeof(vis)); memset(loop,0,sizeof(loop)); cnt = 1;
for(int j = 1,p = 1,ok = 0;j <= n;j ++,p = j)
{
ok = 0;
while(!vis[p])
{
ok = 1;
vis[p] = 1;
p = g[p];
loop[cnt] ++;
}
if(ok) cnt ++;
}
for(int j = 1;j < cnt;j ++) sum[j] = sum[j - 1] + loop[j],id[sum[j]] = j;
int rr,bb,gg,p;
f[0][0][0] = 1;
for(rr = 0;rr <= sr;rr ++)
for(bb = 0;bb <= sb;bb ++)
for(gg = 0;gg <= sg;gg ++) if(p = id[rr + bb + gg])
{
if(rr >= loop[p]) (f[rr][bb][gg] += f[rr - loop[p]][bb][gg]) %= mod;
if(bb >= loop[p]) (f[rr][bb][gg] += f[rr][bb - loop[p]][gg]) %= mod;
if(gg >= loop[p]) (f[rr][bb][gg] += f[rr][bb][gg - loop[p]]) %= mod;
}
(ans += f[sr][sb][sg]) %= mod;
}
printf("%d\n",(ans * pow(m + 1,mod - 2)) % mod);
return 0;
}
[HNOI2008]明明的烦恼:
Prufer序列 + 组合数学
Prufer讲解:
http://www.c*sdn123.com/html/itweb/20130823/78496_78497_78481.htm#csdn123two
先不考虑无解的情况,从 Purfer Sequence 构造树的过程中可知,一个点的度数减一表示它在 Purfer Sequence 中出现了几次,那么:
假设度数有限制的点的数量为 cnt,他们的度数分别为:d[i]
另:
那么,在 Purfer Sequence 中的不同排列的总数为:
而剩下的 n-2-sum 个位置,可以随意的排列剩余的 n-cnt 个点,于是,总的方案数就应该是:
化简之后为:
在有解的情况下,计算该结果输出就行了
无解的情况非常好确定,这里就再讨论了
[HNOI2008]神奇的国度:
最小染色? NP问题? 不,此图为弦图有木有?
弦图详解:
http://wenku.baidu.com/link?url=qHwHbWLnJfgpwntzdb59FeY4i2ZskE1gGAQ6mZU5EecJZn0i7lHayEW0AiySxvcWuRpb7x7ceQZqi59HPXQUJc7namraee2xp1puPrZjz0u
用最大势算法跑出的完美消除序列,然后在此序列中贪心染色即可,贪心染色的部分可参考代码。
不得不吐槽这题的数据了,用暴力的最大势算法居然也能过。。。。
/**************************************************************
Problem: 1006
User: vivym
Language: C++
Result: Accepted
Time:1660 ms
Memory:16624 kb
****************************************************************/
#include
#include
using namespace std;
int tot,head[10000 + 5];
struct Edge
{
int v,nxt;
} e[(1000000 + 2) << 1];
inline void addedge(int u,int v)
{
e[++ tot].v = v,e[tot].nxt = head[u],head[u] = tot;
e[++ tot].v = u,e[tot].nxt = head[v],head[v] = tot;
}
int vis[10000 + 5],lab[10000 + 5],col[10000 + 5],bcol[10000 + 5];
inline int max(int a,int b) { return a > b ? a : b; }
int main()
{
int n,m,u,v;
scanf("%d%d",&n,&m);
for(int i = 0;i < m;i ++) { scanf("%d%d",&u,&v); addedge(u,v); }
int ans = 0;
for(int i = 1;i <= n;i ++)
{
int t = -1,p = 0;
for(int j = 1;j <= n;j ++) if(!vis[j] && t < lab[j]) p = j,t = lab[j];
vis[p] = 1;
for(int k = head[p]; k ;k = e[k].nxt)
{
int v = e[k].v;
if(!vis[v]) lab[v] ++;
else bcol[col[v]] = i;
}
// j 表示第j种颜色 bcol表示第j种颜色的编号
for(int j = 1;j <= n;j ++) if(bcol[j] ^ i) { col[p] = j; ans = max(ans,j); break; }
}
printf("%d\n",ans);
return 0;
}
[HNOI2008]水平可见直线:
斜率排序(不是优化。。。) + 贪心
[HNOI2008]越狱:
组合数学 高考难度
[HNOI2008]GT考试:
……很好的一道Dp + 矩阵加速的题。
f[i][j] : 表示准考证号匹配到第i个,不吉利数匹配到第j(0 <= j < m)个,有多少种方案。
答案就是∑f[n][j](0<=j 唉,可惜我不会转移。。。。。蒟蒻。。。 最后看了看题解。 好吧。利用KMP的pre数组构造个矩阵,然后快速幂。 考虑一下转移,枚举第i+1位填什么,然后用kmp算法的pre数组很快就能得到第i+1位不吉利数匹配到第几位,设为第k位吧,然后把f[i][j]累加到f[i+1][k]中。 然后方程就出来了,f[i][j]=a0*f[i-1][0]+a1*f[i-1][1]+……+am-1*f[i-1][m-1]; 但 n太大了,直接动规不可能,考虑一下不难发现,方程中的系数a与i无关,只与j有关,也就是说每个阶段的状态转移方程是一样的,于是就考虑到了矩阵乘法。先将所有系数处理成一个矩阵mx(用到pre数组),mx[i][j]就表示从f[x-1][i]转移到f[x][j]所乘的系数。然后弄好边界所有的 f[0][j],然后发现,用f[0]这个矩阵(1*m的矩阵)乘以mx矩阵后就能得到f[1](1*m的矩阵),再乘就是f[2]……想到矩阵乘法满足结合律,于是就先用快速幂算出mx这个矩阵的n次方,然后再用f[0]来乘就得到了f[n],然后,然后答案就出来了……复杂度O(m^3*logn)。 for(int i = 0;i < m;i ++) for(int j = 0;j < m;j ++) { int k = i; // a[] : 1 based while(k > 0 && a[k + 1] != j) k = pre[k]; if(a[k + 1] == j) ++ b[i][k + 1]; else ++ b[i][0]; } [HNOI2008]玩具装箱toy: f[i] = min(f[j] + ( (sum[i] – sum[j]) + i – j – 1 - L ) ^ 2) 显然,斜率优化 斜率优化讲解: http://www.cnblogs.com/ka200812/archive/2012/08/03/2621345.html