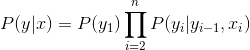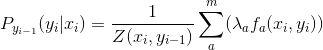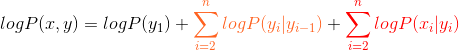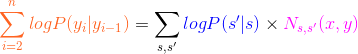【ML】从HMM到CRF，我学到了什么？
目录
可以略过的前言
朴素贝叶斯
条件随机场
最大熵马尔可夫模型
条件随机场
参考
可以略过的前言
以前总结HMM与CRF的区别是什么，只是记住了HMM是生成模型，CRF是条件概率分布模型，深一点的，HMM针对于
建模，而CRF是针对于
建模，至于他们的原理是什么，他们到底在干什么，根本没有弄明白。
希望能借此文，做一些总结和学习，让自己有所提高。若有大佬路过，请多指教！
最近有了一些新的感悟。源于一句话：“凡你能说的，你说清楚；凡你不能说清楚的，留给沉默。”（维特根斯坦，Tractatus）。
本文大量引用了李宏毅老师的教学内容，特此声明。
概率模型
概率模型提供了一种描述框架，将学习任务归结于计算变量的概率分布。在概率模型中，利用已知变量推测未知变量的分布称为“推断”，其核心是如何基于可观测变量推测未知变量的条件分布。
概率图模型是一类用图来表达变量相关关系的概率模型。概率图模型可大致分为两类：
- 使用有向无环图表示变量间的依赖关系，称为有向图模型或贝叶斯网
- 使用无向图表示变量间的相关关系，称为无向图模型或马尔可夫网
朴素贝叶斯
朴素贝叶斯是一个分类模型
朴素贝叶斯基于一个假设：条件独立性假设。这个假设在说，在类别确定的条件下，用于分类的特征是条件独立的。
于是我们可以看到：
马尔可夫模型
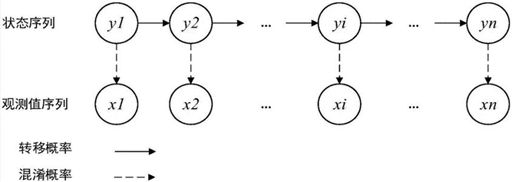
HMM是可用于序列标注（Sequence Labeling）的统计学习模型，是一种结构比较简单的动态贝叶斯网络结构。他描述了由隐藏的状态链生成观测序列的过程，属于生成模型。
场景换到序列标注上来，我们看HMM。序列标注情形如下：（图引自http://speech.ee.ntu.edu.tw/~tlkagk/courses_ML16.html）
在此场景下，HMM是一个建模输入序列到输出序列的模型： 
隐马尔科夫模型由初始状态概率向量
、状态转移矩阵A、和观测概率矩阵（发射矩阵）B决定。用三元符号公式表示:
转移矩阵A中的元素：
,显然在上面的序列标注例子中，转移矩阵是这样的一个方阵，大小为（N，N），N表示当前有多少种标注的可能。每一行代表了时刻
标注为
的状态在
时刻（即下一个词）标注为其他的词
的可能性。
观测概率矩阵B中的元素：
本例中，发射矩阵是一个N*M的矩阵，表示时刻处于状态
的条件下生成
的概率。
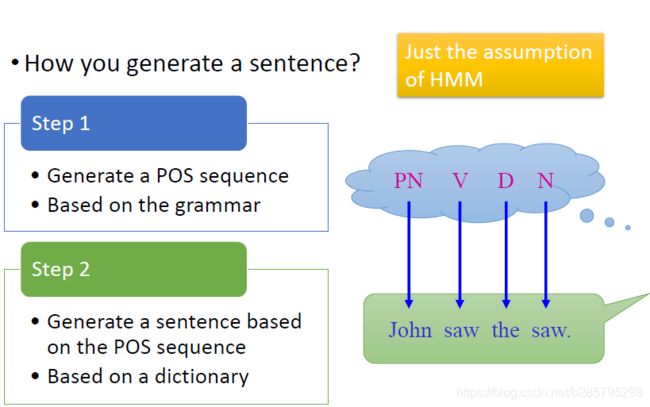
李宏毅老师讲解HMM的例子：
假设我们说出一个句子的过程是这样的：第一步：现在脑海中形成语法链。第二步：根据词汇量匹配语法链。
假设脑中语法知识图是如下形式，我们发现，这个图对应的就是状态转移概率矩阵A，体现的是不同时刻，状态互相转移的概率。自然的，从这个转移矩阵中，我们可以得到一条马尔可夫链（PN->V->D->N）的概率。可以看到，这个"不可观测"的状态序列（PN->V->D->N）的生成是由初始状态概率向量[0.5，0.4，0.1，0，0] 和转移矩阵A共同确定的。
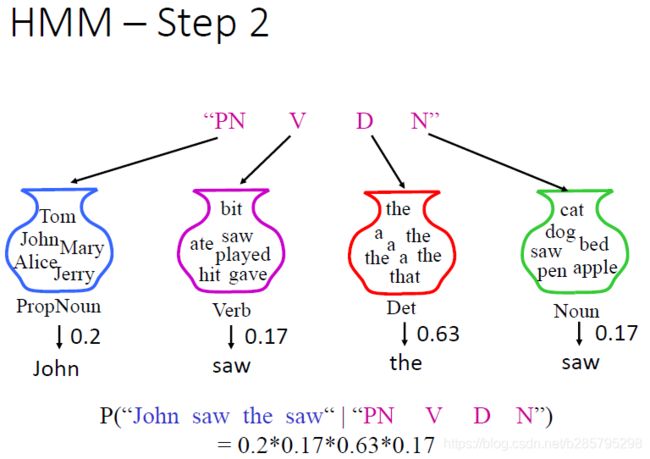
下图表示在状态序列（PN->V->D->N）下生成一句话。即在给定词典中，根据当前时刻的状态，应该选择哪个词汇。从图中我们看到，每一个罐子里面装的是状态序列中某个tag对应的词汇，比如 “PN” 就有['Tom','Jhon','Mary','Alice','Jerry'] 对应，从中选中“John” 的概率为1/2.
这个图对应的实际上就是观测概率矩阵(发射矩阵)B，
表示时刻处于状态 的条件下生成的概率。
此时的发射矩阵，应该是这样子：
| … | saw | … | John | … | Mary | … | ||
| PN | 0 | 0.2 | 0.2 | |||||
| N | 0.17 | |||||||
| … |
那么这个例子中，HMM描述了由状态序列（PN，V，D，N）生成观察序列（John，saw，the，saw）的概率为0.2*0.17*0.63*.17。
那么HMM描述整个序列标注情况的方式可以抽象如下：
更一般的，上图中
我们可以写成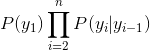 
。于是我们得到HMM中所有变量的联合概率分布为：
。
和 
都很容易从训练数据中求得。
总结：
HMM基于两个假设：
1、观测独立性假设，即任意时刻的观测变量只依赖于此时刻的马尔可夫链状态，与其他观测及状态无关。通俗一点说，t时刻，观测变量
只与此时的有关。
2、齐次马尔科夫假设，即假设隐藏的马尔可夫链在任意时刻的状态只依赖于前一时刻的状态，与其他时刻的状态无关。
比如我t时刻的隐状态 假设是图示的
他只与前一个时刻假设是（
）有关。
这种性质决定了HMM中所有变量的联合概率分布为：
一个标准的HMM需要解决三个基本问题：
- 评估问题，也被称为识别问题。给定模型
和观测序列O，计算每个HMM模型产生当前观测序列的输出概率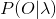 
，通过对比各个模型输出概率，概率最大的模型即为识别结果。（前面所述的整个过程。） - 解码问题。给定模型 和观测序列O，寻找最有可能产生观察序列O的隐含状态序列的过程，即寻找最佳状态序列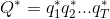
最好地解释观测序列O。（后面给出解释。） - 学习问题。已知观测序列O，估计模型
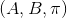参数，使得 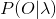最大。（从训练数据中统计即可。）
对于第2点，我们同样可以借助序列标注任务来理解。假设我们现在知道了某一个观察序列x，为['Jhon','saw','the','saw'],怎么找到对应的状态序列y呢？ 即如何求：
。因为：
而
是给定的，那么我们转化为求：
，而
的求法我们已经明确了。
这意味着，原则上，我们只需要将每一个可能的状态序列带入 即带入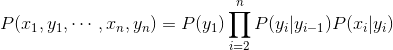，看哪一个序列
能使得 最大。
所以HMM是利用状态转移概率和发射概率计算最优解答，这是一个生成模型。
当然穷举是不可能穷举的，试想假设我们有|S| 个可能的状态，而状态序列的长度为 L., 那么我们显然有
个可能的序列
我们需要Viterbi 算法,一个可以降低复杂度至
的算法。
HMM的不足
预测状态序列的时候，我们做inference时，需要在最优序列
输入时，得到的
一定大于其他序列
对应的。但是实际情况可能不是如此。
如图，比如我们的训练数据中，t-1 到t 时刻的 N->V 的状态序列，产生了t时刻观察状态 c ，这个情况在train data 中出现了9次，将之表示为[N->V=>c] * 9，另外还有[P->V=>a] * 9, [N->D=>a] * 1,那么 当我们已知
时， 最有可能是谁呢？
按照HMM的算法，最优的 是V，但这显然与已有的训练数据 [N->D=>a] 相悖。我们看到没有在训练集出现的（x,y）也有可能产生非常大的概率。产生这种现象是因为HMM中转移（transition probability） 和 发射（Emission probability）是分开建模的。
另外HMM只依赖于每一个状态和它对应的观察对象但是序列标注问题不仅和单个词相关，而且和观察序列的长度，单词的上下文，等等相关。
最大熵马尔可夫模型
MEMM是一种判别式有向图模型。相较于HMM由隐藏状态产生输入（观测），MEMM基于输入（观测）产生隐藏状态（condition on observations）。相比于HMM，MEMM更直观，因为目标是预测出隐藏状态，而不是基于隐藏状态来预测观测。
他打破了HMM的观测独立性假设，直接对条件概率建模，用 
来代替HMM中的两个条件概率
，它表示在先前状态 
，观测值 
下得到当前状态 的概率，即根据前一状态和当前观测。预测当前状态。可以在长距离上得到features。
相比与HMM，MEMM的依旧前一时刻的有关。但他考虑了
的共同作用。
具体建模公式如下：
每个这样的分布函数 
都是一个服从最大熵的指数模型。
这个指数模型让MEMM在 每个状态 
都做了局部归一化，因而可能会产生标注偏置的问题。
举两个例子：
如图所示，“因为”原本应该是介词词性p,而 MEMM却错误标注其词性为连词c。产生该情况的原因正是一种偏置问题。
原因：“是”存在两个词性，动词v和代词r，包含在状态集合
中；“因为”包括两个词性，介词p与连词c，包含在状态集合
中；“事”只有一个词性，名词n，包含在状态集合S3中。由于MEMM对每个状态均定义一个指数模型，因此有：P(n|p)=1, P(n|c)=1, P(p|S1)+P(c|S1)=1; 基于马尔科夫假设，
, 同理，
。因此S2选择p节点还是c节点只取决于P(p|S1)、P(c|S1)，即只与“是”的上下文有关，与“因为”的上下文无关，这即使MEMM产生偏置的一种情况。引自《基于条件随机域的词性标注模型》
条件随机场
若
为观测序列，
为对应的标记序列，则条件随机场的目标是对
建模。通常情况下我们讨论的都是链式条件随机场（CRF）。
设
为线性条件随机场，则在随机变量X取值为 的条件下，随机变量Y取值为的条件概率具有如下形式：
其中，
。
是特征函数，
是权重。
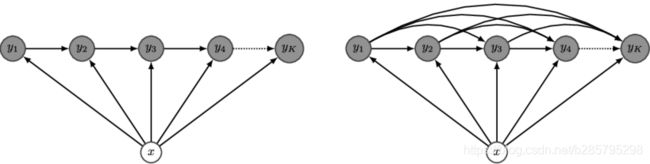
可以看到，相较于MEMM，CRF是无向图模型，全局性的归一化（最大团上的归一化）比于MEMM的局部归一化更优，因而解决了MEMM存在的标注偏置问题。
同时CRF的特征函数定义非常灵活，可以自定义。CRF中的发射概率和HMM的不一样，是，（HMM中是
）.CRF中整个隐藏序列依赖于整个观察序列。
同样跟着李宏毅老师理解CRF,认识CRF的目标函数：
CRF假设观测序列和状态序列 的概率满足 :
,
将从训练数据中学习得到。
根据联合概率与边缘概率分布之间的关系，我们有
,而
,那么：
。这样，我们就建立了conditional model。
就是全局规范化因子。
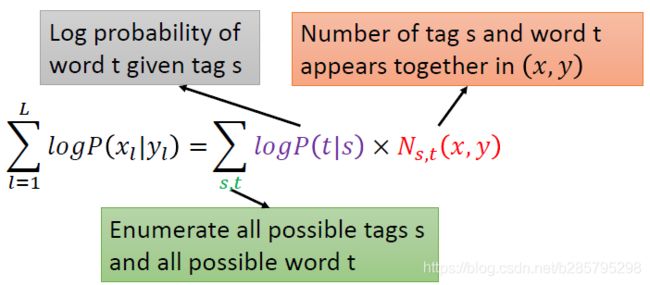
为什么：？他与HMM的函数有多少区别？
我们看HMM的函数：
取log:
在序列标注中,可以有如下的等价关系：
为什么可以这样子转换，可以看下图的示例：
同理：
那么：
所以：
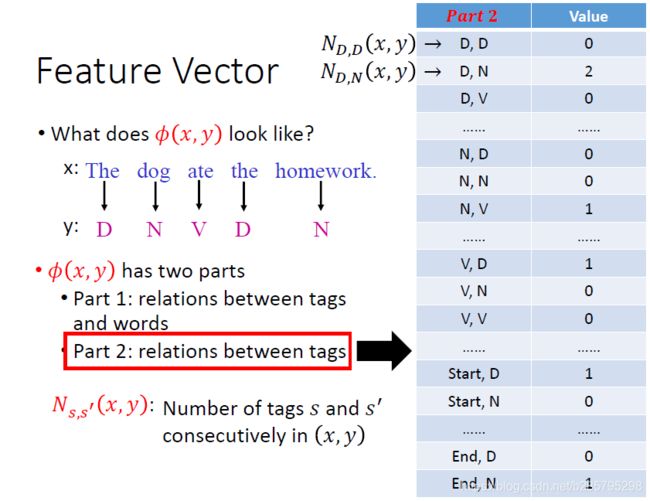
这里直接引用李宏毅老师的课件转述特征函数的一个计算示例：
|S|*|S|+2|S|是因为有start 和 end tag。
关于参数的训练：
CRF比HMM更进一步的，在基于统计的基础上，CRF会调整参数W的值，使之更能fit 数据。
关于bilstmCRF在做序列标注，尤其是NER时，对于CRF的描述，知乎上的回答很中肯：
简单说就是条件随机场可以把label的上下文学出来。lstm加softmax分类的时候只能把特征的上下文关系学出来，label的没学出来。
作者：火华
我理解B-LSTM+CRF模型，所谓在LSTM上面套CRF其实是不严谨的说法，假如这样说，那实际上是两层sequence model了吗。我认为其实是说把LSTM和CRF融合起来。比如LSTM的产出只有发射概率，尽管这个发射概率考虑到了上下文，因为LSTM有门机制，可以记忆或者遗忘前面内容，然后双向，有前有后这样，但是毕竟没有转移概率，像CRF HMM这种，都是结合发射概率和转移概率的。比如在词性标注，最简单BIO这样，有显而易见的规则，就是B-X后面不会有I-Y。所以干脆搞出B-LSTM+CRF，结合发射概率和转移概率这样。实际上后面接的CRF并不是真的CRF，比如它又没有特征模板，它又不接受离散特征，他只是一次Viterbi推导而已。
作者：uuisafresh
链接：https://www.zhihu.com/question/62399257/answer/206903718
参考
- 《机器学习》 周志华
- 《统计学习方法》李航
- HMM MEMM CRF 区别 联系
- hmm-memm-crf
-
【NLP】命名实体识别（NER）的BiLSTM-CRF模型
-
李宏毅sequence labeling