DES

1.DES算法简介

　　DES算法为密码体制中的对称密码体制，又被称为美国数据加密标准。

　　DES是一个分组加密算法，典型的DES以64位为分组对数据加密，加密和解密用的是同一个算法。

　　密钥长64位，密钥事实上是56位参与DES运算（第8、16、24、32、40、48、56、64位是校验位，使得每个密钥都有奇数个1），分组后的明文组和56位的密钥按位替代或交换的方法形成密文组。

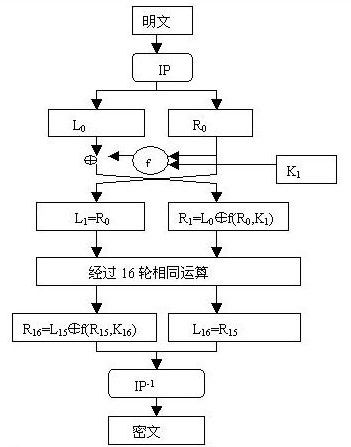
　　DES算法的主要流程如下图所示，本文按照流程依次介绍每个模块。

2.IP置换

　　IP置换目的是将输入的64位数据块按位重新组合，并把输出分为L0、R0两部分，每部分各长32位。

　　置换规则如下表所示：

58	50	42	34	26	18	10	2
60	52	44	36	28	20	12	4
62	54	46	38	30	22	14	6
64	56	48	40	32	24	16	8
57	49	41	33	25	17	9	1
59	51	43	35	27	19	11	3
61	53	45	37	29	21	13	5
63	55	47	39	31	23	15	7

　　表中的数字代表原数据中此位置的数据在新数据中的位置，即原数据块的第1位放到新数据的第58位，第2位放到第50位，……依此类推，第64位放到第7位。置换后的数据分为L0和R0两部分，L0为新数据的左32位，R0为新数据的右32位。

　　设转换前的数据位D1D2D3…D64，则IP置换后的结果为L0=D58D50…D8，R0=D57D49…D7。0x0000 0080 0000 0002转换后的结果为0x0002 0000 0000 0001，且L0=0x0002 0000，R0=0x0000 0001。置换步骤如下：

　　原数据第33位为1，置换表第33位为64，因此将1放到新数据的第64位；原数据第63位为1，置换表第63位为7，因此将1放到新数据的第7位；其余值为0的位按此置换。要注意一点，位数是从左边开始数的，即最0x0000 0080 0000 0002最左边的位为1，最右边的位为64。

3.密钥置换

　　不考虑每个字节的第8位，DES的密钥由64位减至56位，每个字节的第8位作为奇偶校验位。产生的56位密钥由下表生成（注意表中没有8,16,24，32,40,48,56和64这8位）：

57	49	41	33	25	17	9	1	58	50	42	34	26	18
10	2	59	51	43	35	27	19	11	3	60	52	44	36
63	55	47	39	31	23	15	7	62	54	46	38	30	22
14	6	61	53	45	37	29	21	13	5	28	20	12	4

　　在DES的每一轮中，从56位密钥产生出不同的48位子密钥，确定这些子密钥的方式如下：

　　1).将56位的密钥分成两部分，每部分28位。

　　2).根据轮数，这两部分分别循环左移1位或2位。每轮移动的位数如下表：

轮数	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
位数	1	1	2	2	2	2	2	2	1	2	2	2	2	2	2	1

　　移动后，从56位中选出48位。这个过程中，既置换了每位的顺序，又选择了子密钥，因此称为压缩置换。压缩置换规则如下表（注意表中没有9，18，22，25，35，38，43和54这8位）：

14	17	11	24	1	5	3	28	15	6	21	10
23	19	12	4	26	8	16	7	27	20	13	2
41	52	31	37	47	55	30	40	51	45	33	48
44	49	39	56	34	53	46	42	50	36	29	32

         置换方法同上，此处省略。

4.E扩展置换

　　扩展置置换目标是IP置换后获得的右半部分R0，将32位输入扩展为48位(分为4位×8组)输出。

　　扩展置换目的有两个：生成与密钥相同长度的数据以进行异或运算；提供更长的结果，在后续的替代运算中可以进行压缩。

　　扩展置换原理如下表：

32	1	2	3	4	5
4	5	6	7	8	9
8	9	10	11	12	13
12	13	14	15	16	17
16	17	18	19	20	21
20	21	22	23	24	25
24	25	26	27	28	29
28	29	30	31	32	1

　　表中的数字代表位，两列黄色数据是扩展的数据，可以看出，扩展的数据是从相邻两组分别取靠近的一位，4位变为6位。靠近32位的位为1，靠近1位的位为32。表中第二行的4取自上组中的末位，9取自下组中的首位。

　　我们举个例子看一下(虽然扩展置换针对的是上步IP置换中的R0，但为便于观察扩展，这里不取R0举例)：

　　输入数据0x1081 1001，转换为二进制就是0001 0000 1000 0001B，按照上表扩展得下表

1	0	0	0	1	0
1	0	0	0	0	1
0	1	0	0	0	0
0	0	0	0	1	0
1	0	0	0	1	0
1	0	0	0	0	0
0	0	0	0	0	0
0	0	0	0	1	0

　　表中的黄色数据是从临近的上下组取得的，二进制为1000 1010 0001 0100 0000 0010 1000 1010 0000 0000 0000 0010B，转换为十六进制0x8A14 028A 0002。

       扩展置换之后，右半部分数据R0变为48位，与密钥置换得到的轮密钥进行异或。

5.S盒代替

　　压缩后的密钥与扩展分组异或以后得到48位的数据，将这个数据送人S盒，进行替代运算。替代由8个不同的S盒完成，每个S盒有6位输入4位输出。48位输入分为8个6位的分组，一个分组对应一个S盒，对应的S盒对各组进行代替操作。

　　一个S盒就是一个4行16列的表，盒中的每一项都是一个4位的数。S盒的6个输入确定了其对应的输出在哪一行哪一列，输入的高低两位做为行数H，中间四位做为列数L，在S-BOX中查找第H行L列对应的数据(<32)。

　　8个S盒如下：

　　S盒1

14	4	13	1	2	15	11	8	3	10	6	12	5	9	0	7
0	15	7	4	14	2	13	1	10	6	12	11	9	5	3	8
4	1	14	8	13	6	2	11	15	12	9	7	3	10	5	0
15	12	8	2	4	9	1	7	5	11	3	14	10	0	6	13

　　S盒2

15	1	8	14	6	11	3	4	9	7	2	13	12	0	5	10
3	13	4	7	15	2	8	14	12	0	1	10	6	9	11	5
0	14	7	11	10	4	13	1	5	8	12	6	9	3	2	15
13	8	10	1	3	15	4	2	11	6	7	12	0	5	14	9

　　S盒3

10	0	9	14	6	3	15	5	1	13	12	7	11	4	2	8
13	7	0	9	3	4	6	10	2	8	5	14	12	11	15	1
13	6	4	9	8	15	3	0	11	1	2	12	5	10	14	7
1	10	13	0	6	9	8	7	4	15	14	3	11	5	2	12

　　S盒4

7	13	14	3	0	6	9	10	1	2	8	5	11	12	4	15
13	8	11	5	6	15	0	3	4	7	2	12	1	10	14	19
10	6	9	0	12	11	7	13	15	1	3	14	5	2	8	4
3	15	0	6	10	1	13	8	9	4	5	11	12	7	2	14

　　S盒5

2	12	4	1	7	10	11	6	5	8	3	15	13	0	14	9
14	11	2	12	4	7	13	1	5	0	15	13	3	9	8	6
4	2	1	11	10	13	7	8	15	9	12	5	6	3	0	14
11	8	12	7	1	14	2	13	6	15	0	9	10	4	5	3

　　S盒6

12	1	10	15	9	2	6	8	0	13	3	4	14	7	5	11
10	15	4	2	7	12	9	5	6	1	13	14	0	11	3	8
9	14	15	5	2	8	12	3	7	0	4	10	1	13	11	6
4	3	2	12	9	5	15	10	11	14	1	7	6	0	8	13

　　S盒7

4	11	2	14	15	0	8	13	3	12	9	7	5	10	6	1
13	0	11	7	4	9	1	10	14	3	5	12	2	15	8	6
1	4	11	13	12	3	7	14	10	15	6	8	0	5	9	2
6	11	13	8	1	4	10	7	9	5	0	15	14	2	3	12

　　S盒8

13	2	8	4	6	15	11	1	10	9	3	14	5	0	12	7
1	15	13	8	10	3	7	4	12	5	6	11	0	14	9	2
7	11	4	1	9	12	14	2	0	6	10	13	15	3	5	8
2	1	14	7	4	10	8	13	15	12	9	0	3	5	6	11

 

　　例如，假设S盒8的输入为110011，第1位和第6位组合为11，对应于S盒8的第3行；第2位到第5位为1001，对应于S盒8的第9列。S盒8的第3行第9列的数字为12，因此用1100来代替110011。注意，S盒的行列计数都是从0开始。

　　代替过程产生8个4位的分组，组合在一起形成32位数据。

       S盒代替时DES算法的关键步骤，所有的其他的运算都是线性的，易于分析，而S盒是非线性的，相比于其他步骤，提供了更好安全性。

 

6.P盒置换

　　S盒代替运算的32位输出按照P盒进行置换。该置换把输入的每位映射到输出位，任何一位不能被映射两次，也不能被略去，映射规则如下表：

16	7	20	21	29	12	28	17
1	15	23	26	5	18	31	10
2	8	24	14	32	27	3	9
19	13	30	6	22	11	4	25

　　表中的数字代表原数据中此位置的数据在新数据中的位置，即原数据块的第16位放到新数据的第1位，第7位放到第2位，……依此类推，第25位放到第32位。

　　例如0x10A1 0001进行P盒置换后变为0x8000 0886。

　　0x10A1 0001表现为表的形式（第一位位于左上角）原来为

0	0	0	1	0	0	0	0
1	0	1	0	0	0	0	1
0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	1

　　经P盒变换后为

1	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0
0	0	0	0	1	0	0	0
1	0	0	0	0	1	1	0

　　即1000 0000 0000 0000 0000 1000 1000 0110B，十六进制为0x8000 0886。

 

　　最后，P盒置换的结果与最初的64位分组左半部分L0异或，然后左、右半部分交换，接着开始另一轮。

 

7.IP-1末置换

　　末置换是初始置换的逆过程，DES最后一轮后，左、右两半部分并未进行交换，而是两部分合并形成一个分组做为末置换的输入。末置换规则如下表：

40	8	48	16	56	24	64	32
39	7	47	15	55	23	63	31
38	6	46	14	54	22	62	30
37	5	45	13	53	21	61	29
36	4	44	12	52	20	60	28
35	3	43	11	51	19	59	27
34	2	42	10	50	18	58	26
33	1	41	9	49	17	57	25

　　置换方法同上，此处省略。

 

　　经过以上步骤，就可以得到密文了。

 

//DES密码
/*理解算法最重要，最好自己动手实现试试看，可以使用MFC写一个简单的交互界面*/

#include  
#include  
#include  
  
#define BIT bool  
  
using namespace std;  
  
BIT K[16][48];  
  
int   
    //初置换   
    IP[64] = {  
    58 , 50 , 42 , 34 , 26 , 18 , 10 ,  2 ,  
    60 , 52 , 44 , 36 , 28 , 20 , 12 ,  4 ,  
    62 , 54 , 46 , 38 , 30 , 22 , 14 ,  6 ,  
    64 , 56 , 48 , 40 , 32 , 24 , 16 ,  8 ,  
    57 , 49 , 41 , 33 , 25 , 17 ,  9 ,  1 ,  
    59 , 51 , 43 , 35 , 27 , 19 , 11 ,  3 ,  
    61 , 53 , 45 , 37 , 29 , 21 , 13 ,  5 ,  
    63 , 55 , 47 , 39 , 31 , 23 , 15 ,  7},  
    //末置换   
    FP[64] = {  
    40 ,  8 , 48 , 16 , 56 , 24 , 64 , 32 ,  
    39 ,  7 , 47 , 15 , 55 , 23 , 63 , 31 ,  
    38 ,  6 , 46 , 14 , 54 , 22 , 62 , 30 ,  
    37 ,  5 , 45 , 13 , 53 , 21 , 61 , 29 ,  
    36 ,  4 , 44 , 12 , 52 , 20 , 60 , 28 ,  
    35 ,  3 , 43 , 11 , 51 , 19 , 59 , 27 ,  
    34 ,  2 , 42 , 10 , 50 , 18 , 58 , 26 ,  
    33 ,  1 , 41 ,  9 , 49 , 17 , 57 , 25},  
    //密钥置换   
    KP[56] = {  
    57 , 49 , 41 , 33 , 25 , 17 ,  9 ,  1 ,   
    58 , 50 , 42 , 34 , 26 , 18 , 10 ,  2 ,  
    59 , 51 , 43 , 35 , 27 , 19 , 11 ,  3 ,  
    60 , 52 , 44 , 36 , 63 , 55 , 47 , 39 ,  
    31 , 23 , 15 ,  7 , 62 , 54 , 46 , 38 ,  
    30 , 22 , 14 ,  6 , 61 , 53 , 45 , 37 ,  
    29 , 21 , 13 ,  5 , 28 , 20 , 12 ,  4},  
    //密钥位移   
    KM[16] = {  
     1 ,  1 ,  2 ,  2 ,  2 ,  2 ,  2 ,  2 ,   
     1 ,  2 ,  2 ,  2 ,  2 ,  2 ,  2 ,  1},  
    //压缩置换   
    CP[48] = {  
    14 , 17 , 11 , 24 ,  1 ,  5 ,  3 , 28 ,  
    15 ,  6 , 21 , 10 , 23 , 19 , 12 ,  4 ,  
    26 ,  8 , 16 ,  7 , 27 , 20 , 13 ,  2 ,  
    41 , 52 , 31 , 37 , 47 , 55 , 30 , 40 ,  
    51 , 45 , 33 , 48 , 44 , 49 , 39 , 56 ,  
    34 , 53 , 46 , 42 , 50 , 36 , 29 , 32},  
    //扩展置换   
    EP[48] = {  
    32 ,  1 ,  2 ,  3 ,  4 ,  5 ,  4 ,  5 ,  
     6 ,  7 ,  8 ,  9 ,  8 ,  9 , 10 , 11 ,  
    12 , 13 , 12 , 13 , 14 , 15 , 16 , 17 ,  
    16 , 17 , 18 , 19 , 20 , 21 , 20 , 21 ,  
    22 , 23 , 24 , 25 , 24 , 25 , 26 , 27 ,  
    28 , 29 , 28 , 29 , 30 , 31 , 32 ,  1},  
    //S盒   
    S_box[8][4][16] = {  
    //S1     
    {{14,4,13,1,2,15,11,8,3,10,6,12,5,9,0,7},  
    {0,15,7,4,14,2,13,1,10,6,12,11,9,5,3,8},  
    {4,1,14,8,13,6,2,11,15,12,9,7,3,10,5,0},  
    {15,12,8,2,4,9,1,7,5,11,3,14,10,0,6,13}},  
    //S2  
    {{15,1,8,14,6,11,3,4,9,7,2,13,12,0,5,10},  
    {3,13,4,7,15,2,8,14,12,0,1,10,6,9,11,5},  
    {0,14,7,11,10,4,13,1,5,8,12,6,9,3,2,15},  
    {13,8,10,1,3,15,4,2,11,6,7,12,0,5,14,9}},  
    //S3  
    {{10,0,9,14,6,3,15,5,1,13,12,7,11,4,2,8},  
    {13,7,0,9,3,4,6,10,2,8,5,14,12,11,15,1},  
    {13,6,4,9,8,15,3,0,11,1,2,12,5,10,14,7},  
    {1,10,13,0,6,9,8,7,4,15,14,3,11,5,2,12}},  
    //S4  
    {{7,13,14,3,0,6,9,10,1,2,8,5,11,12,4,15},  
    {13,8,11,5,6,15,0,3,4,7,2,12,1,10,14,9},  
    {10,6,9,0,12,11,7,13,15,1,3,14,5,2,8,4},  
    {3,15,0,6,10,1,13,8,9,4,5,11,12,7,2,14}},  
    //S5  
    {{2,12,4,1,7,10,11,6,8,5,3,15,13,0,14,9},  
    {14,11,2,12,4,7,13,1,5,0,15,10,3,9,8,6},  
    {4,2,1,11,10,13,7,8,15,9,12,5,6,3,0,14},  
    {11,8,12,7,1,14,2,13,6,15,0,9,10,4,5,3}},  
    //S6  
    {{12,1,10,15,9,2,6,8,0,13,3,4,14,7,5,11},  
    {10,15,4,2,7,12,9,5,6,1,13,14,0,11,3,8},  
    {9,14,15,5,2,8,12,3,7,0,4,10,1,13,11,6},  
    {4,3,2,12,9,5,15,10,11,14,1,7,6,0,8,13}},  
    //S7  
    {{4,11,2,14,15,0,8,13,3,12,9,7,5,10,6,1},  
    {13,0,11,7,4,9,1,10,14,3,5,12,2,15,8,6},  
    {1,4,11,13,12,3,7,14,10,15,6,8,0,5,9,2},  
    {6,11,13,8,1,4,10,7,9,5,0,15,14,2,3,12}},  
    //S8  
    {{13,2,8,4,6,15,11,1,10,9,3,14,5,0,12,7},  
    {1,15,13,8,10,3,7,4,12,5,6,11,0,14,9,2},  
    {7,11,4,1,9,12,14,2,0,6,10,13,15,3,5,8},  
    {2,1,14,7,4,10,8,13,15,12,9,0,3,5,6,11}}},  
    //P盒  
    PP[32] = {  
    16 ,  7 , 20 , 21 , 29 , 12 , 28 , 17 ,  
     1 , 15 , 23 , 26 ,  5 , 18 , 31 , 10 ,  
     2 ,  8 , 24 , 14 , 32 , 27 ,  3 ,  9 ,  
    19 , 13 , 30 ,  6 , 22 , 11 ,  4 , 25};   
  
void Initial_Permutation(BIT pt[64])  
{  
     BIT tmp[64];  
     for(int i = 0;i < 64;i++)  
             tmp[i] = pt[IP[i]-1];  
     memcpy(pt,tmp,sizeof(tmp));  
     return ;  
}  
  
void Final_Permutation(BIT pt[64])  
{  
     BIT tmp[64];  
     for(int i = 0;i < 64;i++)  
             tmp[i] = pt[FP[i]-1];  
     memcpy(pt,tmp,sizeof(tmp));  
     return ;  
}  
  
void P_Box_Permutation(BIT x[32])  
{  
     BIT tmp[32];  
     for(int i = 0;i < 32;i++)  
             tmp[i] = x[PP[i]-1];  
     memcpy(x,tmp,sizeof(tmp));  
     return ;       
}  
       
void Generate_K(BIT SK[64])  
{  
     BIT L[60],R[60];  
     int i,j,st;  
       
     memset(K,0,sizeof(K));  
  
     for(i = 0;i < 28;i++)  
             L[i+28] = L[i] = SK[KP[i]-1],  
             R[i+28] = R[i] = SK[KP[i+28]-1];  
     st = 0;  
     for(i = 0;i < 16;i++) {  
             st += KM[i];  
             for(j = 0;j < 48;j++)  
                     K[i][j] = (CP[j] < 28)?L[CP[j] + st - 1]:R[CP[j] - 29 + st];  
             }  
     return ;  
}  
  
void Work(BIT L[32],BIT R[32],BIT KEY[48],int cnt)  
{  
     BIT X[48],RES[32];  
     memset(RES,0,sizeof(RES));  
     memset(X,0,sizeof(X));  
     int i,j,a,b,st,st2,tmp;  
       
     for(i = 0;i < 48;i++)  
          X[i] = R[EP[i]-1] ^ KEY[i];  
          
     for(i = 0;i < 8;i++) {  
   
           st = i * 6;  
           a = (X[st] << 1) + X[st + 5];  
           b = (X[st + 1] << 3) + (X[st + 2] << 2) + (X[st + 3] << 1) + X[st + 4];   
           tmp = S_box[i][a][b];  
           st2 = i * 4;  
           for(j = 0;j < 4;j++)  
                 RES[st2 + (3 - j)] |= (tmp >> j)&1;  
           }  
  
      P_Box_Permutation(RES);  
        
      for(i = 0;i < 32;i++)  
            L[i] ^= RES[i];  
  
      if (cnt == 15) return ;  
  
      BIT temp[32];  
      
      memcpy(temp,L,sizeof(temp));  
      memcpy(L,R,sizeof(temp));  
      memcpy(R,temp,sizeof(temp));  
        
      return ;    
}  
  
void DES_enc(char txt[10],char enc[10])  
{  
     int i,j;  
     BIT L[32],R[32];  
     BIT pt[64];  
  
     for(i = 0;i < 8;i++)  
          for(j = 7;j >= 0;j--)  
                pt[i * 8 + (7 - j)] = (txt[i] >> j) & 1;  
  
     Initial_Permutation(pt);  
  
     for(i = 0;i < 32;i++)  
           L[i] = pt[i],R[i] = pt[i + 32];  
  
     for(i = 0;i < 16;i++)  
           Work(L,R,K[i],i);  
  
     for(i = 0;i < 32;i++)  
           pt[i] = L[i],pt[i + 32] = R[i];  
             
      
     Final_Permutation(pt);  
  
     for(i = 0;i < 8;i++)  
           for(j = 7;j >= 0;j--)  
                 enc[i] |= pt[i * 8 + (7 - j)] << j;    
  
     return ;              
}  
  
void DES_dec(char txt[10],char dec[10])  
{  
     int i,j;  
     BIT L[32],R[32];  
     BIT pt[64];  
       
     for(i = 0;i < 8;i++)  
          for(j = 7;j >= 0;j--)  
                pt[i * 8 + (7 - j)] = (txt[i] >> j) & 1;  
  
     Initial_Permutation(pt);  
  
     for(i = 0;i < 32;i++)  
           L[i] = pt[i],R[i] = pt[i + 32];  
  
     for(i = 0;i < 16;i++)  
           Work(L,R,K[15 - i],i);  
  
     for(i = 0;i < 32;i++)  
           pt[i] = L[i],pt[i + 32] = R[i];  
             
     Final_Permutation(pt);  
       
     for(i = 0;i < 8;i++)  
           for(j = 7;j >= 0;j--)  
                 dec[i] |= pt[i * 8 + (7 - j)] << j;    
  
     return ;              
}    
  
void DES_E()  
{  
     int tmp,i,j;  
     BIT sk[64];  
     char txt[10],key[10],res[10];  
     char Fpt[100],Fct[100];  
     FILE *P,*O;  
  
     printf("Plase enter the plaintext file:");  
     scanf("%s",Fpt);  
     printf("Plase enter the key:");  
     scanf("%s",key);  
     printf("Plase enter the ciphertext file:");  
     scanf("%s",Fct);  
       
     for(i = 0;i < 8;i++)  
          for(j = 7;j >= 0;j--)  
                sk[i * 8 + (7 - j)] = (key[i] >> j) & 1;       
            
     Generate_K(sk);  
       
     P = fopen(Fpt,"r");  
     O = fopen(Fct,"w");  
     while(tmp = fread(txt,sizeof(txt[0]),8,P)) {  
       for(i = tmp;i < 8;i++) txt[i] = 0;  
           memset(res,0,sizeof(res));  
       DES_enc(txt,res);  
           fwrite(res,sizeof(res[0]),8,O);  
           }  
     fclose(O);  
     fclose(P);  
     return ;  
}  
  
void DES_D()  
{  
     int tmp,i,j;  
     BIT sk[64];  
     char txt[10],key[10],res[10];  
     char Fpt[100],Fct[100];  
     FILE *P,*O;  
  
     printf("Plase enter the ciphertext file:");  
     scanf("%s",Fpt);  
     printf("Plase enter the key:");  
     scanf("%s",key);  
     printf("Plase enter the plaintext file:");  
     scanf("%s",Fct);  
  
     for(i = 0;i < 8;i++)  
          for(j = 7;j >= 0;j--)  
                sk[i * 8 + (7 - j)] = (key[i] >> j) & 1;       
            
     Generate_K(sk);  
  
     P = fopen(Fpt,"r");  
     O = fopen(Fct,"w");  
     while (tmp = fread(txt,sizeof(txt[0]),8,P)) {  
       for(i = tmp;i < 8;i++) txt[i] = 0;  
           memset(res,0,sizeof(res));  
       DES_dec(txt,res);  
           fwrite(res,sizeof(res[0]),8,O);  
           }  
     fclose(O);  
     fclose(P);  
     return ;  
}  
  
int main()  
{  
    char str[10];  
    while(1){  
             printf("选择模式---加密(E) 或 解密(D)---：");  
             scanf("%s",str);  
             if (str[0] == 'D') DES_D();  
             else if (str[0] == 'E') DES_E();  
             else return 0;              
             printf("OK...O^_^O\n");  
             }  
}