Stanford-CS231n-assignment1-two_layer_net附中文注释

先记录一个很好用的画神经网络图的网站：http://alexlenail.me/NN-SVG/index.html

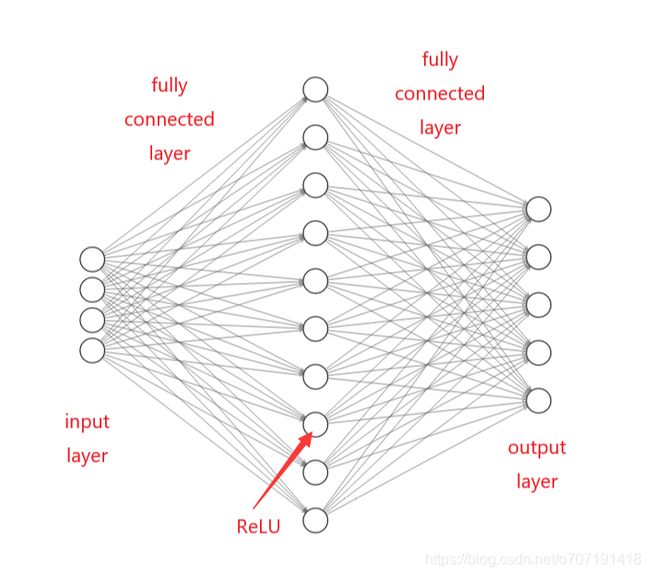
然后因为对神经网络的几个层的名字到底应该标注在哪有点疑惑，现在看了几段代码才弄清楚，所以标注在图上记录一下，如下图（激活函数以ReLU为例），如果错误欢迎指正

神经网络各层名

上图中的神经网络可叫做双层（应该是双全连接层）神经网络或者单隐藏层（one hidden layer）网络。网络的前向传播方式为输入节点与W1权重矩阵相乘并加上偏置b1，得到隐藏层的输入值，然后隐藏层的输入值需要经过ReLU函数处理，得到隐藏层的输出函数，然后再用输出函数重复上述过程，乘以W2权重矩阵并加上偏置b2，得到输出层的值。在这个过程中需要注意矩阵的维度方向，很容易颠倒出错，导致维度不一致无法相加或者相乘。

1. neural_net.py

1.1 Q1

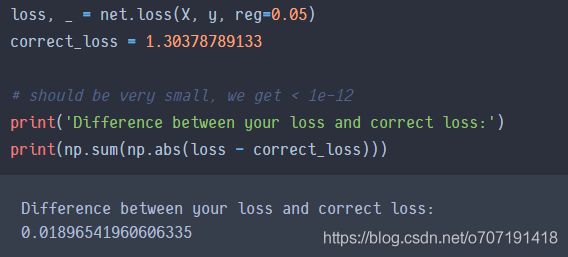
第一个问题，在第一次求Loss的地方，出现了这个结果

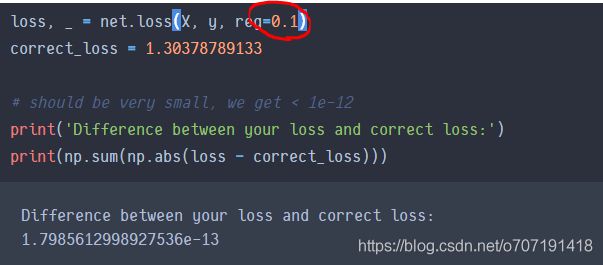
我的代码每次跑都是0.018，感觉这个差值有点大了，然后去网上看别人的代码都是e-13级别的差值，然后在代码里找问题找了好久，实在找不出来错误，然后用别人的代码跑也是上面0.018这个结果，最后在这篇博客https://blog.csdn.net/kammyisthebest/article/details/80377613中看到，人家的reg都是0.1，我们的是0.05？？？然后reg改成0.1跑了一遍，果不其然

1.2 Q2

第二个问题，在求解神经网络反向传播的梯度代码中，遇到一个问题，求W1/W2的梯度都不难理解，但是求b1/b2的梯度时候就遇到问题了，首先代码中前向传播是这样写的

# 输入值与W1的点积，作为下一层的输入
z2 = X.dot(W1) + b1
# 激活函数，求得隐藏层的输出，也就是ReLU
a2 = np.maximum(z2, 0)
# 隐藏层的输出进入到输出层
scores = a2.dot(W2) + b2

这样乍得一看，好像b1/b2的偏导数都是数字1，这导致我第一次写b1/b2的时候直接把偏导写成了np.ones_like(b1/b2)，后来想想，不对啊，这只是在代码中用numpy库的简化写法罢了，实质上应该这么写

# 其实偏置本来也应该是一个矩阵，但是在Numpy的计算中直接被简化了
z2 = X.dot(W1) + np.ones(N).dot(b1.reshape(H, -1))  # 只是表达这个意思，代码不一定能跑
a2 = np.maximum(z2, 0)
scores = a2.dot(W2) + np.ones(N).dot(b2.reshape(C, -1))

 也就是说在求b1/b2的偏导数时候，实质上求导应该得到的是一个np.ones(N)这么一个向量，然后再根据cs231n中的求导法则，用上游传回来的偏导值乘以本地函数值，就可以得到梯度，也就是下面的代码

# 先求出输出层softmax型的loss func对输出层的偏导数，作为反向传播的起点，此处与SVM相同
# softmax公式为L=-s[yi]+ln(∑e^s[j])，可以求得L对s[yi]的偏导数为-1+e^s[yi]/∑e^s[j]，也就是下面代码中的-1+prob
# 由于输出层的z和a是相同的值（即a==z），所以此处delta(L)/delta(a) == delta(L)/delta(z)
output = np.zeros_like(scores)
output[range(N), y] = -1
output += prob
# 先根据反向传播的上层梯度乘以本地变量求出W2的梯度
grads['W2'] = (a2.T).dot(output) # 公式BP4
grads['W2'] = grads['W2'] / N + reg * W2
# 求取b2的梯度，方法同上
grads['b2'] = np.ones(N).dot(output) / N

1.3 代码

from __future__ import print_function

from builtins import range
from builtins import object
import numpy as np
import matplotlib.pyplot as plt
from past.builtins import xrange

class TwoLayerNet(object):
    """
    A two-layer fully-connected neural network. The net has an input dimension of
    N, a hidden layer dimension of H, and performs classification over C classes.
    We train the network with a softmax loss function and L2 regularization on the
    weight matrices. The network uses a ReLU nonlinearity after the first fully
    connected layer.

    In other words, the network has the following architecture:

    input - fully connected layer - ReLU - fully connected layer - softmax

    The outputs of the second fully-connected layer are the scores for each class.
    """

    def __init__(self, input_size, hidden_size, output_size, std=1e-4):
        """
        Initialize the model. Weights are initialized to small random values and
        biases are initialized to zero. Weights and biases are stored in the
        variable self.params, which is a dictionary with the following keys:

        W1: First layer weights; has shape (D, H)
        b1: First layer biases; has shape (H,)
        W2: Second layer weights; has shape (H, C)
        b2: Second layer biases; has shape (C,)

        Inputs:
        - input_size: The dimension D of the input data.
        - hidden_size: The number of neurons H in the hidden layer.
        - output_size: The number of classes C.
        """
        self.params = {}
        self.params['W1'] = std * np.random.randn(input_size, hidden_size)
        self.params['b1'] = np.zeros(hidden_size)
        self.params['W2'] = std * np.random.randn(hidden_size, output_size)
        self.params['b2'] = np.zeros(output_size)

    def loss(self, X, y=None, reg=0.0):
        """
        Compute the loss and gradients for a two layer fully connected neural
        network.

        Inputs:
        - X: Input data of shape (N, D). Each X[i] is a training sample.
        - y: Vector of training labels. y[i] is the label for X[i], and each y[i] is
          an integer in the range 0 <= y[i] < C. This parameter is optional; if it
          is not passed then we only return scores, and if it is passed then we
          instead return the loss and gradients.
        - reg: Regularization strength.

        Returns:
        If y is None, return a matrix scores of shape (N, C) where scores[i, c] is
        the score for class c on input X[i].

        If y is not None, instead return a tuple of:
        - loss: Loss (data loss and regularization loss) for this batch of training
          samples.
        - grads: Dictionary mapping parameter names to gradients of those parameters
          with respect to the loss function; has the same keys as self.params.
        """
        # Unpack variables from the params dictionary
        W1, b1 = self.params['W1'], self.params['b1']
        W2, b2 = self.params['W2'], self.params['b2']
        N, D = X.shape

        # Compute the forward pass
        scores = None
        #############################################################################
        # TODO: Perform the forward pass, computing the class scores for the input. #
        # Store the result in the scores variable, which should be an array of      #
        # shape (N, C).                                                             #
        #############################################################################
        # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
        
        # 输入值与W1的点积，作为下一层的输入
        z2 = X.dot(W1) + b1
        # 激活函数，求得隐藏层的输出，也就是ReLU
        a2 = np.maximum(z2, 0)
        # 隐藏层的输出进入到输出层
        scores = a2.dot(W2) + b2
        pass

        # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

        # If the targets are not given then jump out, we're done
        if y is None:
            return scores

        # Compute the loss
        loss = None
        #############################################################################
        # TODO: Finish the forward pass, and compute the loss. This should include  #
        # both the data loss and L2 regularization for W1 and W2. Store the result  #
        # in the variable loss, which should be a scalar. Use the Softmax           #
        # classifier loss.                                                          #
        #############################################################################
        # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

        # 根据softmax的Loss函数定义来求该网络的Loss
        # 先减去最大值防止数值错误
        scores -= np.max(scores, axis=1, keepdims=True)
        # 求所有得分项求自然指数
        exp_scores = np.exp(scores)
        # 求概率矩阵
        prob = exp_scores / np.sum(exp_scores, axis = 1, keepdims=True)
        # 取出分类正确项的概率
        correct_items = prob[range(N), y]
        # 根据softmax的loss func求loss
        data_loss = -np.sum(np.log(correct_items)) / N
        reg_loss = 0.5 * reg * (np.sum(W1 * W1) + np.sum(W2 * W2))
        loss = data_loss + reg_loss
        pass

        # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

        # Backward pass: compute gradients
        grads = {}
        #############################################################################
        # TODO: Compute the backward pass, computing the derivatives of the weights #
        # and biases. Store the results in the grads dictionary. For example,       #
        # grads['W1'] should store the gradient on W1, and be a matrix of same size #
        #############################################################################
        # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

        # 先求出输出层softmax型的loss func对输出层的偏导数，作为反向传播的起点，此处与SVM相同
        # softmax公式为L=-s[yi]+ln(∑e^s[j])，可以求得L对s[yi]的偏导数为-1+e^s[yi]/∑e^s[j]，也就是下面代码中的-1+prob
        # 由于输出层的z和a是相同的值（即a==z），所以此处delta(L)/delta(a) == delta(L)/delta(z)
        output = np.zeros_like(scores)
        output[range(N), y] = -1
        output += prob
        # 先根据反向传播的上层梯度乘以本地变量求出W2的梯度
        grads['W2'] = (a2.T).dot(output) # 公式BP4
        grads['W2'] = grads['W2'] / N + reg * W2
        # 求取b2的梯度，方法同上
        grads['b2'] = np.ones(N).dot(output) / N
        # 将最后一层节点的误差反向传播至隐藏层
        hidden = output.dot(W2.T)
        # 考虑到ReLU函数的作用，可以知道只有在z2矩阵中大于零的部分才会被传递至后面的层中，这里求的就是ReLU函数的偏导矩阵
        mask = np.zeros_like(z2)
        mask[z2 > 0] = 1
        hidden = hidden * mask # N*H，这里相当于求解出了how bp algorithm works那一章中的公式BP2
        # 再从隐藏层反向传播至W1
        grads['W1'] = (X.T).dot(hidden) # 公式BP4
        grads['W1'] = grads['W1'] / N + reg * W1
        # W1同理
        grads['b1'] = np.ones(N).dot(hidden) / N
        pass

        # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

        return loss, grads

    def train(self, X, y, X_val, y_val,
              learning_rate=1e-3, learning_rate_decay=0.95,
              reg=5e-6, num_iters=100,
              batch_size=200, verbose=False):
        """
        Train this neural network using stochastic gradient descent.

        Inputs:
        - X: A numpy array of shape (N, D) giving training data.
        - y: A numpy array f shape (N,) giving training labels; y[i] = c means that
          X[i] has label c, where 0 <= c < C.
        - X_val: A numpy array of shape (N_val, D) giving validation data.
        - y_val: A numpy array of shape (N_val,) giving validation labels.
        - learning_rate: Scalar giving learning rate for optimization.
        - learning_rate_decay: Scalar giving factor used to decay the learning rate
          after each epoch.
        - reg: Scalar giving regularization strength.
        - num_iters: Number of steps to take when optimizing.
        - batch_size: Number of training examples to use per step.
        - verbose: boolean; if true print progress during optimization.
        """
        num_train = X.shape[0]
        iterations_per_epoch = max(num_train / batch_size, 1)

        # Use SGD to optimize the parameters in self.model
        loss_history = []
        train_acc_history = []
        val_acc_history = []

        for it in range(num_iters):
            X_batch = None
            y_batch = None

            #########################################################################
            # TODO: Create a random minibatch of training data and labels, storing  #
            # them in X_batch and y_batch respectively.                             #
            #########################################################################
            # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

            # 加上replace=False时候提示Cannot take a larger sample than population when 'replace=False'，即batch_size>num_train时错误，故去掉
            random_index = np.random.choice(num_train, batch_size) 
            X_batch = X[random_index, :]
            y_batch = y[random_index]
            pass

            # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

            # Compute loss and gradients using the current minibatch
            loss, grads = self.loss(X_batch, y=y_batch, reg=reg)
            loss_history.append(loss)

            #########################################################################
            # TODO: Use the gradients in the grads dictionary to update the         #
            # parameters of the network (stored in the dictionary self.params)      #
            # using stochastic gradient descent. You'll need to use the gradients   #
            # stored in the grads dictionary defined above.                         #
            #########################################################################
            # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

            self.params['W1'] -= grads['W1'] * learning_rate
            self.params['W2'] -= grads['W2'] * learning_rate
            self.params['b1'] -= grads['b1'] * learning_rate
            self.params['b2'] -= grads['b2'] * learning_rate
            pass

            # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

            if verbose and it % 100 == 0:
                print('iteration %d / %d: loss %f' % (it, num_iters, loss))

            # Every epoch, check train and val accuracy and decay learning rate.
            if it % iterations_per_epoch == 0:
                # Check accuracy
                train_acc = (self.predict(X_batch) == y_batch).mean()
                val_acc = (self.predict(X_val) == y_val).mean()
                train_acc_history.append(train_acc)
                val_acc_history.append(val_acc)

                # Decay learning rate
                learning_rate *= learning_rate_decay

        return {
          'loss_history': loss_history,
          'train_acc_history': train_acc_history,
          'val_acc_history': val_acc_history,
        }

    def predict(self, X):
        """
        Use the trained weights of this two-layer network to predict labels for
        data points. For each data point we predict scores for each of the C
        classes, and assign each data point to the class with the highest score.

        Inputs:
        - X: A numpy array of shape (N, D) giving N D-dimensional data points to
          classify.

        Returns:
        - y_pred: A numpy array of shape (N,) giving predicted labels for each of
          the elements of X. For all i, y_pred[i] = c means that X[i] is predicted
          to have class c, where 0 <= c < C.
        """
        y_pred = None

        ###########################################################################
        # TODO: Implement this function; it should be VERY simple!                #
        ###########################################################################
        # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

        # 前向传播，求出输出值
        z2 = X.dot(self.params['W1']) + self.params['b1']
        a2 = np.maximum(z2, 0)
        scores = a2.dot(self.params['W2']) + self.params['b2']
        # 求出得分矩阵每一行最大值的索引，代表分类的类别
        y_pred = np.argmax(scores, axis=1)
        pass

        # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

        return y_pred

 

 

2. two_layer_net.ipynb

best_net = None # store the best model into this 

#################################################################################
# TODO: Tune hyperparameters using the validation set. Store your best trained  #
# model in best_net.                                                            #
#                                                                               #
# To help debug your network, it may help to use visualizations similar to the  #
# ones we used above; these visualizations will have significant qualitative    #
# differences from the ones we saw above for the poorly tuned network.          #
#                                                                               #
# Tweaking hyperparameters by hand can be fun, but you might find it useful to  #
# write code to sweep through possible combinations of hyperparameters          #
# automatically like we did on the previous exercises.                          #
#################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
best_acc = 0
learning_rate = [1e-4, 5e-4, 1e-3]
regulations = [0.2, 0.25, 0.3, 0.35]
for lr in learning_rate:
    for reg in regulations:
        stats = net.train(X_train, y_train, X_val, y_val,
            num_iters=1500, batch_size=200,
            learning_rate=lr, learning_rate_decay=0.95,
            reg=reg, verbose=True)
        val_acc = (net.predict(X_val) == y_val).mean()
        if val_acc > best_acc:
            best_acc = val_acc
            best_net = net
            print('lr = ',lr ,' reg = ',reg, ' acc = ', best_acc)
pass

# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

 

昨天晚上跑的时候在val集上最高的准确率达到了0.527，但是最后的参数出错，好像因为learning_rate设置太大导致nan错误，不知道为什么0.527的best_net也没有保存下来，今天再跑，最高的准确率只有0.52了，

然后最终在test_set上的测试结果