K-means算法、EM算法——斯坦福CS229机器学习个人总结(五)
这一份总结的主题是无监督学习的EM算法。
在前面提到的逻辑回归、SVM、朴素贝叶斯等算法,他们的训练数据都是带有标签的(预分类结果),这样的算法被称为监督学习。当训练数据没有标签,只提供特征时,称为无监督学习。
EM算法(Expectation maxmization algorithm,最大期望算法)就是一种无监督学习算法,而它的名字本身就已经包含了这个算法的特点以及做法——“期望”、“最大化”。
下面会从背后包含着强大EM算法思想的K-means算法开始,抛砖引玉,再介绍EM算法本身。
1、K-means聚类算法(The k-means clustering algorithm)
聚类算法是最常见的无监督算法,对于一组无标签数据,可以用聚类算法去发掘数据中的隐藏结构。聚类算法应用广泛,举例来说,对基因进行聚类,可以发掘不同物种中具有相同功能的基因片段;对顾客行为进行聚类,可以发掘出顾客的喜好情况,制定相应的促销策略;对新闻进行聚类,使得描述同一件事的报道不全部展示;在图片分割中,可以利用图片不同部分的相似性来理解图片信息等。
K-means算法就是一种聚类算法,给定没有标签的输入数据 {x(1),x(2),⋯,x(m)} ,K-means算法的聚类过程如下:
①随机选择K个聚类质心为 μ1,μ2,⋯,μk∈Rn
②重复下面过程直到收敛{
E-step、对于每一个样本 i ,计算其应该属于的类
c(i):=argminj∥∥x(i)−μj∥∥2
M-step、对于每一个被分类的 j ,重新计算该类的质心位置
μj:=∑mi=1I{c(i)=j}x(i)∑mi=1I{c(i)=j}
}
下图展示对两个质心进行聚类的过程。
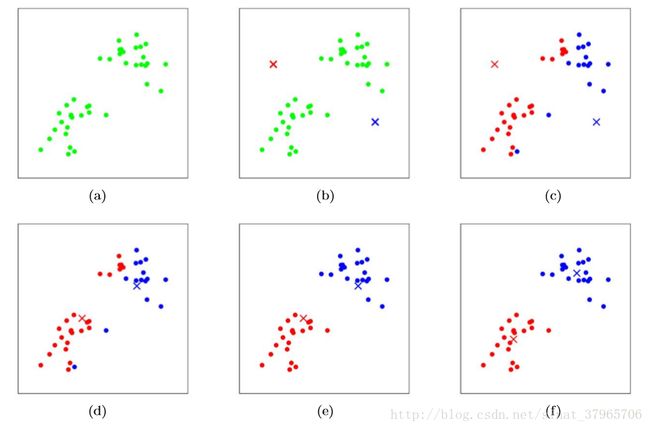
图一
(a)原始数据
(b)随机初始化的两个质心红叉与蓝叉
(c)E-step,距离红叉更近的标记为红色,距离蓝叉更近的标记为蓝色
(d)M-step,根据红色类与蓝色类计算距离的平均值,更新质心(红叉与蓝叉)的位置
(e)E-step,距离红叉更近的标记为红色,距离蓝色更近的标记为蓝色
(f)M-step,根据红色类与蓝色类计算距离的平均值,更新质心(红叉与蓝叉)的位置
到了这里,如果再继续重复E步与M步,质心的位置也不会再发生变化,这表示算法已经收敛,聚类结束。
对于K-means算法来说,它要优化的目标函数路看成如下形式:
J 函数表示每个样本点到其质心距离的平方和,K-means算法的目标是把它调到最小。可以想象,如果是样本点分类变了,证明它离该分类质心更近了(E-step);如果质心位置变了,那么属于这一类的样本到质心的距离整体变小了(M-step)。
由于 J 函数不是凸函数,所以它的局部最优不一定是全局最优。为了达到更好的效果可以随机初始化多次质心的位置,取最小的 J 中对应的参数输出。
如果聚类结束后,某个质心附近没有任何属于它的样本,可以将这个质心删除,或者是重新初始化。
2、EM算法(Expectation maxmization algorithm,最大期望算法)
2.1、EM算法概述
EM算法是一个实实在在的算法,但是在我的理解中,它跟核函数、牛顿法类似,是一种计算的技巧,是为了解决某种计算问题而存在的——当我们进行最大似然估计的时候,如果该似然函数不能直接求解(求解困难或者无解),我们可以使用EM算法来求取其极值——这只是EM算法众多应用中的一种,但是就课程上能接触到的东西来说,我会按照这个思路做下去。
那么EM算法是如何对不能直接求解的似然函数取极值的?

图二(Ng在课上画的图)
l(θ) 表示一个对数似然性,我们尝试使它最大化,通常情况下直接对它求导并令其导数为0这样的计算是十分困难的。
EM算法的做法是:
初始化一个 θ(0) ,建立一个对数似然函数比较紧的下界,在猜测参数之后,会满足某个不等式的约束,我们会使这个下界参数最大化,于是得到了该下界的最大化参数 θ(1) ,然后对 θ(1) 创建一个新的下界,再使这个下界最大化得到 θ(2) ,重复这些步骤直到收敛到函数的一个局部最优值。而对数函数是凹函数,它拥有凸函数局部最优即全局最优的性质,所以该局部最优值就是对数似然性 l(θ) 的最大值。
2.2、EM算法的推导
2.2.1、Jensen不等式(Jensen’s inequality)
在正是开始EM算法的推导之前,在这里先介绍一个肯定会用到的定理,即Jensen不等式:
若 f 为凸函数, X 为一随机变量,有
f(EX) 是 f(E[X]) 的简写。
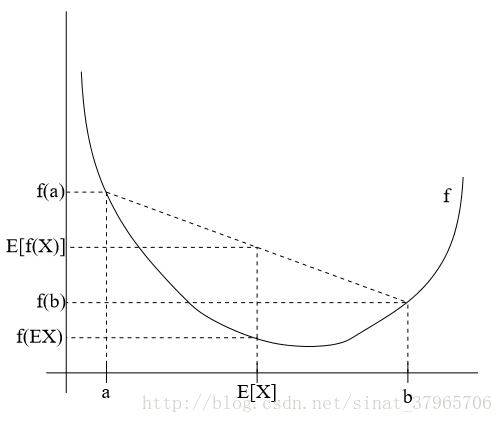
图三
Jensen不等式可以这样推出来:
函数 f 是凸函数的充要条件是 f′′(x)≥0 (或者 H≥0 , H 为Hessien矩阵),此时式(1)成立。
进一步地,若 f′′(x)>0 (或者 H>0 ),函数 f 被称为严格凸函数,则当且仅当 X=E(X) 时,式(1)Jensen不等式的等号成立,此时 X 是一个常量。(若 f′′(x)=0 ,图像可以是一段与 x 轴平行的线,这样的函数不是严格凸函数)
若 f′′(x)≤0 或者 H≤0 时,函数 f 是凹函数,此时的Jensen不等式也成立,但是不等号的方向要反转,有:
同样对于严格凹函数,以上所述也成立。
2.2.1、EM算法
2.2.1.1、E-step——由期望(Expectation)与Jensen不等式建立下界
求解某不能直接求解的似然函数
给定训练样本 {x(1),⋯,x(m)} ,样本独立,对其似然函数取对数,有
引入隐藏变量 z
如果直接求解这个似然函数异常麻烦或者无解,我们可以引入一个隐藏变量 z ,并且 p(x(i)|z(i)) 与 p(z(i)) 分别服从某个分布:
假设 z 服从 Q 分布
对于每一个样本 i ,令 z(i) 满足某个分布 Qi(z(i)) ,其中 Qi 满足 ∑zQi(z)=1,Qi(z)≥0 ,并且如果 z 是连续的,那么 Qi 是概率密度函数,需要将求和符号换成积分符号。
引入 Qi 后:
使用Jensen不等式与期望的定义
我们来观察一下式(8)。
如果把式(8)当成一个 log 的函数, f(x)=logx ,我们有 f′′(x)=−1x2<0 ,即式(8)是一个严格凹函数;
另外,由期望的定义:若 x ~ p(x) , E[g(x)]=∑xp(x)g(x) ,又因为 z(i) ~ Qi(z(i)) ,所以可以把 Qi(z(i)) 看成 p(z(i)) ,并且式(8)中 ∑zQi(z(i))[p(x(i),z(i);θ)Qi(z(i))] 这个式子看成是 g(z(i))=[p(x(i),z(i);θ)Qi(z(i))] 的期望,再由式(5)凹函数下的Jensen不等式,我们可以继续往下推导:
至此,我们得到了这样的结论:
这样,我们就建立了一个所要最大化的目标函数 l(θ) 的下界函数,对应着图二中 l(θ) 曲线下的若干小曲线(比如 θ0 对应的那个小曲线,就是一个下界)。
利用严格凹函数的性质取Jensen不等式的等号与 Q 分布
在上文有提到, f(x)=logx 是一个严格凹函数( f′′(x)=−1x2<0 ),那么当 X=E(X) 的时候,式(9)的不等号可以取等号(来自上文Jensen不等式的定义)。
当等号成立的时候,最大化下界就相当于在最大化目标函数 l(θ) 。
同时, X=E(X) ( X 为常数)在式(9)中意味着:
这表示 Qi(z(i)) 正比于 p(x(i),z(i);θ) (为了方便我们把这个比例定为1),同时有 ∑zQi(z)=1 ( Q 是一个分布),所以我们可以得到:
如此, Q 分布实际上是一个后验概率,到这里,我们的下界也真正确立下来了。
2.2.1.2、M-step——最大化(Maxmize)下界
由此,EM算法的步骤如下:
循环直到收敛{
E-step:对于每一个样本 i ,计算
Qi(z(i)):=p(z(i)∣x(i);θ)
M-step:计算
θ:=argmaxθ∑i∑zQi(z(i))logp(x(i),z(i);θ)Qi(z(i))
}
M步的具体计算按实际问题的分布而定。
2.2.1.3、EM算法的收敛性
我们如何得知EM算法的收敛性?这里给出简单证明。
假设当前的参数为 θ(t) ,此时对这个下界进行最大似然估计,就能得到参数 θ(t+1) ,并且由式(10),我们有:
所以我们有 l(θ(t+1))≥l(θ(t)) (最后一个等号成立的条件是式(11)),表示 EM算法是单调递增的。
如图二所示,如果我们最大化 θ(0) 对应的下界函数,得到 θ(1) ,再通过 θ(1) 建立一个新的下界,再次最大化,那么我们的下界将会渐渐靠近目标函数 l(θ) 的最大值,当函数收敛时,我们就得到了目标函数 l(θ) 的最大值。
2.2.1.4、用坐标上升法理解EM算法
在EM算法的一般化形式中,可以将目标函数看作是坐标上升的过程:
在E-step中, θ 不变,调整 Q 使目标函数变大;
在M-step中, Q 不变,调整 θ 使目标函数变大。