oj1344题求和：对于正整数n,k，我们定义这样一个函数f，它满足如下规律：······现在给出n和k，你的任务就是要计算f(n,k)的值。

原题：

分析即实现

这是一道数学题，我们很容易想到，只要找到了这个函数的解析式，这个问题便可以迎刃而解，加上计算机强大的计算能力，该题应当是可以很快完成计算的，然后可以观察这个式子，得到an的表达式：

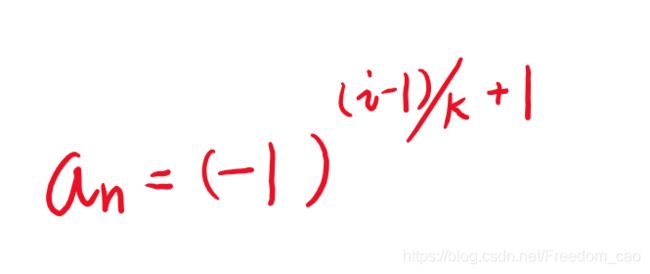
然后逐项叠加，于是我们便有了以下解法：

#include <iostream>
#include <cmath>
using namespace std;

long long solve(long long n,long long k)
{
     
	long long num=0; 
	for (long long i=1;i<=n;i++)
		num+=pow(-1,(i-1)/k+1)*i;
	return num;
}
int main()
{
     
	int T;
	cin >> T;
	long long n;
	long long k;
	while(T--)
	{
     
		cin >> n >> k;
		cout << solve(n,k) << endl;
	}
	return 0;
}

可惜的是，oj报不通过，超时了，想想也是，pow（）函数会花费不少的时间，于是我便思考如何消掉这个pow（）函数，于是最终写出来以下代码：

#include <iostream>
using namespace std;

long long solve(long long n,long long k)
{
     
	long long num=0; 
	for(long long i=1;i<=n;i++)
	{
     
		if (((i-1)/k+1)%2!=0)
			num+=(-i);
		else
			num+=i;
	}
	return num;
}
int main()
{
     
	int T;
	cin >> T;
	long long n,k;
	while(T--)
	{
     
		cin >> n >> k;
		cout << solve(n,k) << endl;
	}
	return 0;
}

该方法的思想和第一种是一样的，但是消掉了pow函数，心想这次一定可以通过了，奈何再次爆出超时警告，噗，心累啊！怎么办？再想想，能不能换一种方法。
第三种方法：
可以将k看成一个小周期，2k看成一个大周期，那n/2k就表示大周期的个数，每个大周期的值很容易知道是k*k，那么我们很容易知道前面这个部分的值就是n/2k * k^2,再加上后面多出的部分就是结果，于是我又可以写出一个代码：

#include <iostream>
using namespace std;

long long solve(long long n,long long k)
{
     
	long long x=n/(2*k)*k*k;
	long long a=n%(2*k),b=n-a+1;
	if (n%(2*k)==0)
		return x;
	else if (a/(k+1)==0)
	{
     
		for (long long i=b;i<=n;i++)
			x+=(-i);
		return x;
	}
	else
	{
     
		for (long long i=b;i<b+k;i++)
			x+=(-i);
		for (long long i=b+k;i<=n;i++)
			x+=i;
		return x;
	}
}
int main()
{
     
	int T;
	cin >> T;
	long long n;
	long long k;
	while(T--)
	{
     
		cin >> n >> k;
		cout << solve(n,k) << endl;
	}
	return 0;
}

哈哈，终于通过了！
小提示：
在做这个题的时候，我最开始用int定义，最后发现越界，所以大家在写oj时千万要注意使用long long哦！
ps：
这三个代码经过测试，都是正确的，但是在oj上跑的话，1和2都超时了，只有3可以完美通过。
如果对你有帮助的话，不妨点个赞再走呗！