【数据结构与算法Python描述】——树的简介、基本概念和手动实现一个二叉树

在之前的文章中，不论是列表还是链表，抑或是基于二者实现的栈、队列等数据结构都是线性结构，即元素之间只有“前”和“后”的关系，从本文开始我们将学习最重要的一种非线性数据结构之一——树，这类数据结构可表达更加丰富的对象间关系，从而可以更好地对更多的现实场景进行抽象。

一、树的简介

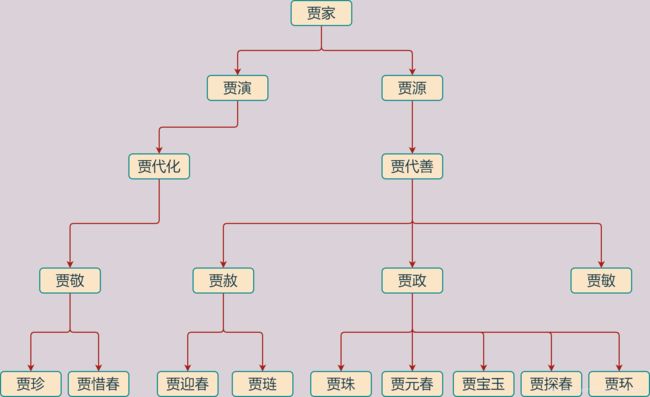
现实中用树形结构描述信息的案例很多，例如下图所示的《红楼梦》中贾家的家谱图：

1. 树的定义

正式地，当某一个由保存了对象元素的结点所组成的集合满足下列两条性质时，我们将该集合抽象定义为数据结构树T：

• 如果T非空，则其有一个被称为根结点的特殊结点，该结点没有父结点；
• T中每一个不是根结点的结点v都有且仅有唯一的一个父结点w。

例如，就上述的《红楼梦》中贾家家谱图来看：

• 贾家是根结点，该结点没有父节点；
• 除贾家外的其他所有结点都有且仅有一个父结点（这也很好理解，因为所有人都只有一个父亲）。

实际上，根据上述定义，树T还有如下递归特性：树T要么空，要么包含根结点r以及一系列根结点为结点r的子结点的子树（子树可能为空）。

2. 相关概念

除了上述关于树以及根结点的定义外，还有以下将用于后续讨论的重要概念：

• 兄弟结点：具有同一个父结点的结点之间互为兄弟结点，例如：贾演和贾源、贾珠和贾宝玉；
• 外部结点：没有子结点的结点，例如：贾环；
• 内部结点：有一个或多个子结点的结点；
• 叶子结点：外部结点又称叶子结点；
• 祖先结点：对于两个结点u和v，如果u = v或者u是v的父结点的祖先结点，则结点u是v的祖先结点，例如：从贾宝玉自身到贾政、贾代善、贾源直到贾家都是贾宝玉结点的祖先结点；
• 子孙结点：与祖先结点的概念相对；
• 边：对于一对结点(u, v)，如果u是v的父结点或v是u的父结点，则称(u, v)是树T的一条边，例如：(贾敬, 贾珍)就是一条边；
• 路径：路径是这样一个结点序列，即序列中任意相邻的两个结点都可形成一条边，例如：(贾家, 贾源, 贾代善, 贾政, 贾宝玉)就是一条路径；
• 有序树：如果树的每一个结点的子结点之间都存在有意义线性关系，则这样的树被称为有序树，例如：上述贾家的家谱图就是一个有序树，因为每一父结点的子结点都按照人员年龄大小从左到右排列。

二、树的ADT

本文仍然采用文章【数据结构与算法Python描述】——位置列表简介与Python版手工实现中描述位置的方式来抽象地表示树中每一个结点：即每个对象元素都保存在每一个抽象位置处，树的结点关系由结点间的位置来表示。则树ADT至少支持以下非修改类方法：

方法	功能
__len__()	返回树T中的对象元素个数
__iter__()	生成树T的所有保存的对象元素的一个迭代
T.root()	返回树T的根结点位置，当T为空返回None
T.is_root(p)	如果p是树T的根结点则返回True
T.parent(p)	返回位置p处的结点的父结点所在位置，当p为根结点位置则返回None
T.children(p)	生成位置p处结点的所有子结点的一个迭代
T.num_children(p)	返回位置p处结点的子结点数目
T.is_leaf(p)	如果位置p处的结点无任何子结点则返回True
T.is_empty()	如果树T不包含任何结点则返回True
T.positions()	生成树T中所有位置的一个迭代

需要注意的是：

• 类似文章【数据结构与算法Python描述】——位置列表简介与Python版手工实现中使用_Position的实例描述某结点在位置列表中的位置所遇到的情况，如果一个位置实例描述树T中某一个位置的行为不合法，则应该抛出ValueError异常；
• 位置p对象仅支持一个方法element()，即p.element()返回该位置代表的结点处的对象元素；
• 如果树T为有序的，则T.children(p)按照位置p处所有子结点内在顺序进行迭代返回。

三、树的实现准备

对于树的ADT本文不会像之前的数据结构文章一样直接对其进行具体实现，下面指出之前的论述方法所存在的部分问题：

首先，下列三篇文章分别使用列表、单向线性链表以及单向循环链表作为对象元素存储容器实现了队列这一数据结构：

• 【数据结构与算法Python描述】——队列和双端队列简介及其高效率版本Python实现
• 【数据结构与算法Python描述】——单向线性链表简介、Python实现及应用
• 【数据结构与算法Python描述】——单向循环链表简介、Python语言实现及应用

问题在于，分析上述三种实现方式的代码后可知：

• 不同实现的ADT一致但彼此间未建立关联，因为这些具体实现本身就是以队列的ADT为蓝本；
• 不同实现中部分方法的实现完全一样（如：is_empty()、__len__()等）。

针对上述两个问题，很自然地需要考虑：

• 是否可以将针对同一数据结构ADT的不同实现关联起来；
• 是否可以降低不同实现间的代码重复度。

实际上，Python中的抽象基类就可用于解决上述两个问题，即使用抽象基类：

• 表达某一数据结构的ADT；
• 实现不同实现中的共有和实用方法。

1. 树的基本分类

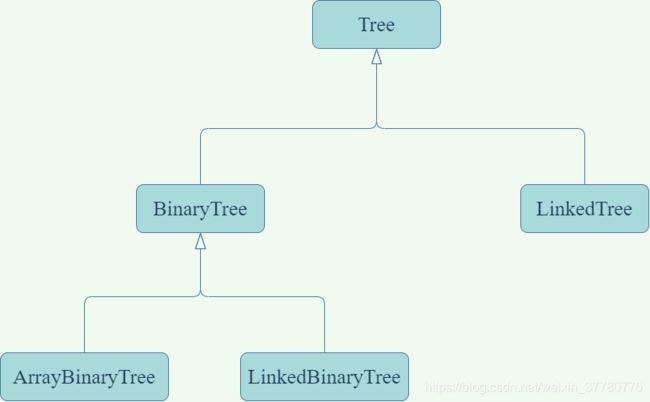
对于树定义抽象基类的另一个考虑是，截至目前本文讨论的都是一般性的树，但实际使用最多的是二叉树BinaryTree，即所有结点的子结点数量不大于2个的一类树，且根据使用列表还是链表实现，又可以分为ArrayBinaryTree和LinkedBinaryTree，而上述给出的非修改类方法组成的ADT适用于所有类型的树。

因此将上述ADT封装在一个抽象基类Tree中，实现BinaryTree时只需继承Tree即可，而实现ArrayBinaryTree和LinkedBinaryTree只需继承BinaryTree并实现抽象方法即可。

2. 树的抽象基类

基于Python中的继承、抽象基类和接口定义抽象基类的方法，下面给出一般树的抽象基类完整定义。

from abc import ABCMeta, abstractmethod


class Tree(metaclass=ABCMeta):
    """表示一般树的抽象基类"""

    class Position(metaclass=ABCMeta):
        """嵌套定义的位置类，其实例对象用于描述结点在树中的位置"""

        @abstractmethod
        def element(self):
            """
            用于返回某位置处的对象元素
            :return: 结点处的对象元素
            """

        @abstractmethod
        def __eq__(self, other):
            """
            使用'=='判断两个Position实例是否代表同一个位置
            :param other: 另一个Position的实例
            :return: Boolean
            """

        @abstractmethod
        def __ne__(self, other):
            """
            使用'!='判断两个Position实例是否不代表同一个位置
            :param other: 另一个Position的实例
            :return: Boolean
            """
    
    @abstractmethod
    def __len__(self):
        """
        返回树中所有结点数量
        :return: 结点数量
        """
        
    @abstractmethod
    def root(self):
        """返回代表数根结点的位置对象，如树为空则返回None"""
        
    @abstractmethod
    def parent(self, p):
        """
        返回位置p处结点的父结点所在位置，如p处为根结点则返回None
        :param p: 某结点所在位置
        :return: 某结点的父结点所在位置
        """
    
    @abstractmethod
    def num_children(self, p):
        """
        返回位置p处结点的子结点数目
        :param p: 结点位置
        :return: 结点的子结点数目
        """
        
    @abstractmethod
    def children(self, p):
        """
        生成位置p处结点的所有子结点的一个迭代
        :param p: 结点位置
        :return: 子结点位置
        """

    @abstractmethod
    def __iter__(self):
        """生成一个树的结点元素的迭代"""
        
    @abstractmethod
    def positions(self):
        """生成一个树的结点位置的迭代"""
        
    def is_root(self, p):
        """如果位置p处的结点为根结点则返回True"""
        return self.root() == p
    
    def is_leaf(self, p):
        """如果位置p处的结点无任何子结点则返回True"""
        return self.num_children(p) == 0
    
    def is_empty(self):
        """如果树为空，则返回True"""
        return len(self) == 0

分析上述代码可知：

• 用于描述位置的Position类以嵌套的方式定义在了Tree的内部，且其中的方法也均定义为了抽象方法；
• 对上述树的所有ADT方法，多数都定义为了抽象方法，而is_root()、is_leaf()、is_empty()这几个方法虽然定义为普通方法，但其实现依赖于其他抽象方法，实际上这体现了算法设计中常用的一种设计模式——模板方法设计模式。

四、树的概念拾遗

除前面提及的和树相关定义，树以及其结点还有两个重要概念：深度和高度。

1. 深度

• 普通定义：如果p为树T的某结点位置，则对于位置p处的结点，其除自身外的所有祖先结点数量称为位置p处结点的高度。
• 递归定义：
  • 如果位置p处为根结点，则该位置处的结点深度为0；
  • 如果位置p处不是根结点，则该位置处的结点深度等于其父结点深度加1。

基于上述树的递归定义，可以在上述Tree中添加一个递归方法depth()以通过给定树T的位置p来计算该位置的结点高度：

def depth(self, p):
    """
    返回位置p处结点的高度
    :param p: 结点位置
    :return: 结点高度
    """
    if self.is_root(p):
        return 0
    else:
        return 1 + self.depth(self.parent(p))

上述depth()方法的时间复杂度为$O(d_p+1)$，其中$d_p$表示位置p处结点的深度，因为该算法的递归次数和当前位置处结点的祖先结点（结点自身为自身的祖先结点）数量相同，而每次递归均使用定长时间。

实际上，如果树T中结点总数为$n$，则上述depth()方法的最坏时间复杂度为$O(n)$，此时树T的所有结点仅形成一条分支。虽然depth()方法的运行时间与树T的结点个数$n$呈函数关系，但通常我们使用结点深度$d_p$作为函数参数：

• 一方面这更直观；
• 另一方面$d_p$通常小于$n$。

2. 高度

递归定义：仿照结点深度的递归定义，结点高度的递归定义为：

• 如果位置p处为叶子结点，则该结点高度为0；
• 如果位置p处不为叶子结点，则该结点高度为其所有子结点中最大的高度加1。

一般也将树T的根结点高度称为树的高度，而一个非空树T的高度等于其所有叶子结点深度中的最大值。

下面使用结点高度的递归定义在Tree中给出一个最坏时间复杂度为$O(n)$（其中$n$为树T结点数量）的结点高度计算方法_height()：

def _height(self, p):
    """
    返回位置p处结点的高度
    :param p: 结点位置
    :return: 结点高度
    """
    if self.is_leaf(p):
        return 0
    else:
        return 1 + max(self._height(child) for child in self.children(p))

下面分析为什么说_height()的最坏时间复杂度为$O(n)$：

虽然我们至此还未实现T.children()方法，但后续可知对该方法有最坏时间复杂度为$O(c_p+1)$的实现，其中$c_p$为位置p处结点的子结点数量，基于此下面分析为什么说_height()的最坏时间复杂度为$O(n)$：

• 上述_height()实现中每一个位置处递归调用的最坏时间复杂度为$O(c_p+1)$；
• 当位置p代表根结点时，上述_height()方法递归总次数最大，此时达到算法的最坏情况。

因此，此时所有位置处的时间复杂度和为$O({\sum }_p(c_p+1))=O({\sum }_p{c}_p+n)$，而如果$c_p$代表任意位置p处的子结点数量，则${\sum }_p{c}_p=n-1$，因此上述_height()实现的最坏时间复杂度为$O(n)$。

上述_height()方法可以使用结点位置p计算其高度，而实际中使用最多的是计算整个树T的高度，为了避免每次都显式指定p为根结点位置，可以如下所示重新定义一个height()方法，在其中调用非公有方法_height()：

def _height(self, p):
    """
    返回位置p处结点的高度
    :param p: 结点位置
    :return: 结点高度
    """
    if self.is_leaf(p):
        return 0
    else:
        return 1 + max(self._height(child) for child in self.children(p))
    
def height(self, p=None):
    """
    返回位置p处结点的高度，默认返回根结点高度
    :param p: 结点位置
    :return: 结点高度
    """
    if p is None:
        p = self.root()
    return self._height(p)

五、二叉树的简介

1. 定义

基本定义：二叉树是每个结点至多有两个子结点的有序树。

基于上述定义一般将一个结点的两个子结点分别称为左子结点和右子结点，左和右的区分以两个结点的自然顺序划分，如：本文开头红楼梦家谱图（需要注意这不是二叉树，但不妨碍以此为例）中，贾珍和贾惜春作为贾敬的子结点，如果其中所有人都之多有两个子女，则因为贾珍年长于贾惜春，因此贾珍为左子结点，贾惜春为右子结点。

除此之外，关于二叉树还有如下几个概念：

• （左）右子树：以（左）右子结点为根结点的子树；
• （非）完全二叉树：每一个结点都有0个或两个子结点的二叉树。

基于上述概念，还可以给出二叉树的递归定义：

递归定义：一个树T为空或其满足下列要求时该树为二叉树：

• 包含一个根结点r；
• 根结点r有一个左子树（可能为空），该子树为二叉树；
• 根结点r有一个右子树（可能为空），该子树也为二叉树。

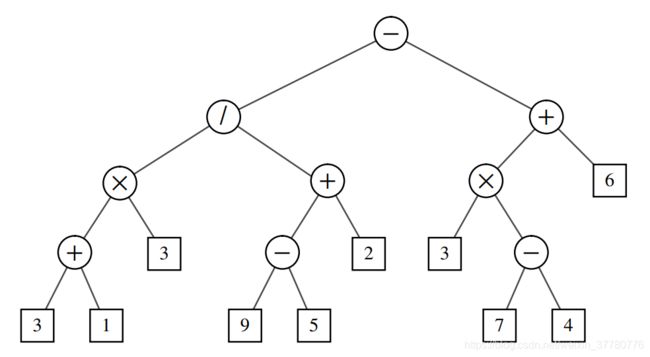
实际上，完全二叉树的案例有很多，如下面的决策树以及数学表达式：

2. 性质

3. ADT

4. 抽象基类

六、二叉树的实现

七、一般树的实现