【数据结构与算法Python描述】——队列和双端队列简介及其高效率版本Python实现
文章目录
- 一、队列
-
- 1. 队列的定义
- 2. 队列的原型
- 3. 队列的ADT
- 4. 队列的实现
-
- 4.1 循环使用列表
- 4.2 使用列表实现队列
-
- a. 入队方法代码分析
- b. 出队方法代码分析
- c. 倍增底层列表长度
- d. 减半底层列表长度
- 4.3 队列操作复杂度分析
- 二、双端队列
-
- 1. 双端队列的定义
- 2. 双端队列的原型
- 3. 双端队列的ADT
- 4. 双端队列的实现
-
- 4.1 循环使用列表实现双端队列
- 5. `collection`模块的`deque`类
一、队列
队列是另外一个基本的数据结构,队列是和文章【数据结构与算法Python描述】——栈的简介与实现中介绍的栈这种数据结构的近亲,二者十分相似。
1. 队列的定义
队列是一组对象元素的集合,队列中的元素在插入和删除时遵循先进先出(FIFO: First-in, first-out)的原则,即某一元素可以在任何从队尾插入,但是该元素只有当处于队头是才可以被删除。
2. 队列的原型
如果要用现实中的场景来描述队列的原型,可以使用常见的排队模型来表示,例如:在电影院售票、商场收银台等地方,所有顾客排队享受服务,不管你何时到达队列处,你都要从队尾开始排队(这叫“入队”),而只有当你排到了队列的第一位你才可以买到票或结账然后离开队伍(这叫“出队”)。
3. 队列的ADT
基于上述对于队列定义和原型的描述,可以知道队列的ADT中至少包含下列两个方法:
Q.enqueue(e):向队列Q的队尾添加元素e;Q.dequeue():从队列Q的队头删除并返回第一个元素,当队列为空时抛出异常。
同样,为了更方便地使用队列,还需要在其ADT中定义以下实用方法:
Q.first():返回队列Q的队头元素但不将其删除,如果此时队列为空,则抛出异常;Q.is_empty():如果此时队列中无任何元素,则返回True;__len__():重写__len__()方法并让其返回队列Q中的元素个数,使得len(Q)可以返回队列的元素个数。
4. 队列的实现
在文章【数据结构与算法Python描述】——栈的简介与实现中,我们通过将Python的列表用作存储栈元素,并使用适配器设计模式的思想,设计了一个Stack类。因此,我们第一反应可能是使用类似策略来实现队列的ADT,即:
- 使用列表的
append(e)方法来实现队列的enqueue(e)方法; - 使用列表的
pop(0)方法来实现从队头删除并返回一个元素的方法dequeue()。
遗憾的是,虽然上述实现方式十分简单,但其效率却也十分低下,原因在于:在文章【数据结构与算法Python描述】——Python列表实现原理深入探究及其常用操作时间复杂度分析中,通过分析列表的底层原理,我们知道使用pop(0)删除元素时,由于每删除列表的第一个元素时,其后的所有元素每个都需要向右平移一个单元,因此时间复杂度至少为 O ( n ) O(n) O(n)。
既然使用列表的pop(0)方法实现dequeue()有上述严重缺陷,可以继续考虑这样的一种思路:在每调用一次dequeue()时都将队头单元修改为引用None,并且使用变量front保存下一个单元(此时该单元为队头)的索引。如此一来,dequeue()操作的时间复杂度就只是 O ( 1 ) O(1) O(1)了。
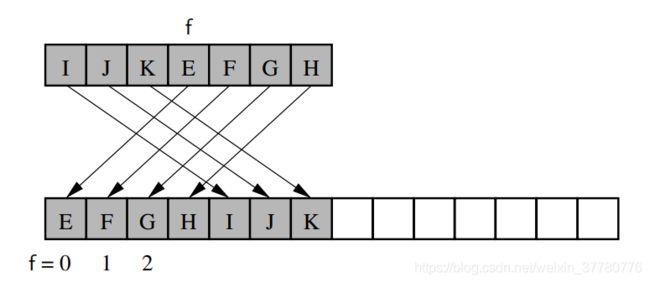
实际上,上述实现dequeue()的算法虽然时间上效率较高,但是却十分浪费内存资源,例如:使用上述方法实现dequeue()后,使用enqueue(e)和dequeue()将字母表中字符进行一系列入队和出队操作之后,其内存模型大致如下所示:
需要注意的是:上述为简便期间,示意图将字符保存在了每一个单元处,实际上由【数据结构与算法Python描述】——字符串、元组、列表内存模型简介可知,Python列表中由索引标识的每一个单元处保存了字符在内存的地址(这就是所谓索引的含义),地址处才保存了每一个字符。
也就是说,经过一系列的入队和出队操作后,用于存储元素用的列表长度将增长至 O ( m ) O(m) O(m),其中 m m m是自队列创建以来,执行enqueue(e)和dequeue()操作的总次数,而非当前队列中的元素个数。
4.1 循环使用列表
最终,为了实现一个兼具高效且节省内存的dequeue()方法,可以考虑将因出队操作而引用None的单元重复利用起来,即如果经过一系列入队和出队的操作后,此时队尾已和底层列表的最右单元重合,且此时队头的前方有若干引用None的单元,此时调用enqueue('I')时,底层列表索引为0的单元将引用'I',下一次调用enqueue('J')时,底层列表索引为1的单元将引用'J',以此类推。
上面的描述如下图所示:
由上述分析可知,实现dequeue()的关键分别在于:实现元素每次入队操作后,front代表的索引值加1,且还要在front为底层列表最大索引值且其最左侧有引用None的单元时,front的值可以重新从0开始递增,直至列表元素满溢。
对于上述需要,可以使用一个简单的数学表达式front = (front + 1) % N来实现,其中%是所谓的取余操作,N是底层列表最大容量。例如:现有一个长度为10的列表,如果此时:
front为7,则执行一次dequeue()操作后,则front = (7 + 1) % 10的结果为8;front为9,则执行一次dequeue()操作后,则front = (9 + 1) % 10的结果为0。
4.2 使用列表实现队列
根据上述一系列分析,这里给出使用Python列表实现队列的完整代码,在ListQueue内部定义了下列三个实例属性:
_data:一个具有固定长度的列表实例的引用;_size:一个整数,表明当前队列实例中的元素个数;_front:一个整数,代表了_data中存储队头元素的列表单元索引(假定此时队列不为空)。
对于上述三个实例属性,当创建一个空队列时,_data的初始长度为适当的值如10,队列的长度_size为0,队头所对应的列表索引_front也为0。
另外,由于要求队列为空时,调用队列first()和dequeue()方法均抛出异常,则类似文章【数据结构与算法Python描述】——栈的简介与实现,也自定义同样的异常类型Empty。
下面是使用Python列表作为元素存储容器实现队列的完整代码:
class Empty(Exception):
"""尝试对空队列执行pop()或top()操作时抛出的异常"""
pass
class ListQueue:
"""遵循FIFO原则的队列实现,使用Python列表作元素存储用"""
DEFAULT_CAPACITY = 10 # 为新创建队列分配的适当大小
def __init__(self):
"""创建新的空队列时的初始化方法"""
self._data = [None] * ListQueue.DEFAULT_CAPACITY
self._size = 0
self._front = 0
def __len__(self):
"""
返回队列中元素个数
:return: int
"""
return self._size
def __str__(self):
"""
以无歧义的方式返回栈的字符串表示形式
:return: 底层列表的字符串表示形式
"""
return str(self._data)
def is_empty(self):
"""
队列为空时返回True,否则返回False
:return: Boolean
"""
return self._size == 0
def first(self):
"""
返回但不删除队头元素,当队列为空时抛出Empty异常
:return: 队头元素
"""
if self.is_empty():
raise Empty('队列当前为空!')
return self._data[self._front]
def dequeue(self):
"""
按照FIFO(先进先出)的原则删除并返回队头元素,当队列为空时抛出Empty异常
:return: 队头元素
"""
if self.is_empty():
raise Empty('队列当前为空!')
ans = self._data[self._front]
self._data[self._front] = None # 协助解释器进行GC(Garbage Collection)
self._front = (self._front + 1) % len(self._data) # 将队头所对应列表索引值加1或归零
self._size -= 1
return ans
def enqueue(self, e):
"""
向队尾插入一个元素
:param e: 待插入队尾的元素
:return: None
"""
if self._size == len(self._data): # 用于存储队列元素的底层列表是否已满
self._resize(2 * len(self._data)) # 将列表长度翻倍
avail = (self._front + self._size) % len(self._data)
self._data[avail] = e
self._size += 1
def _resize(self, capacity):
"""
调整用于存储队列元素的底层列表长度
:param capacity: 期望的列表长度
:return: None
"""
old_lst = self._data # 记录原始列表的引用
self._data = [None] * capacity # 分配新的列表,并将其作为存储队列元素的容器
walk = self._front
for k in range(self._size): # 循环将旧列表元素拷贝至新列表
self._data[k] = old_lst[walk]
walk = (1 + walk) % len(old_lst)
self._front = 0 # 将队头和新列表的第一个单元对齐
def main():
lst_queue = ListQueue()
lst_queue.enqueue(5)
print(lst_queue) # [5, None, None, None, None, None, None, None, None, None]
lst_queue.enqueue(3)
print(lst_queue) # [5, 3, None, None, None, None, None, None, None, None]
lst_queue.enqueue(1)
print(lst_queue) # [5, 3, 1, None, None, None, None, None, None, None]
print(len(lst_queue)) # 3
print(lst_queue.dequeue()) # 5
print(lst_queue) # [None, 3, 1, None, None, None, None, None, None, None]
print(lst_queue.is_empty()) # False
print(lst_queue.first()) # 3
if __name__ == '__main__':
main()
上述代码中,方法__len__()以及is_empty()的实现均较为直观,first()方法的实现也比较简单,因为_front所表示的索引可以精确地确定队头元素在列表_data中的位置(假定此时队列非空)。
a. 入队方法代码分析
enqueue(e)方法用于向队尾插入元素,实现该方法的关键在于确定应该向底层列表的哪一个索引处放入该元素的索引。上述代码中尽管没有显式地为队尾维护一个实例属性,但我们可以使用下列公式计算得到该索引:
avail = (self.front + self.size) % len(self.data)
对于上述公式,可以通过具体举例来理解,假设有一个容量为10的队列:
- 如果当前元素个数为3,队头元素在对应底层数组索引5的单元处,因此队列中的3个元素依次保存在列表索引为5,6,7的单元处,则新入队的元素应该保存在数组索引 ( 5 + 3 ) % 10 = 8 (5+3)\%{10}=8 (5+3)%10=8的单元处;
- 如果当前元素个数为3,队头元素在对应底层数组索引8的单元处,队列中的3个元素依次保存在列表索引为8,9,0的单元处,则新入队的元素应该保存在数组索引 ( 8 + 3 ) % 10 = 1 (8+3)\%{10}=1 (8+3)%10=1的单元处。
b. 出队方法代码分析
当调用队列的dequeue()方法时,self._front当前的值就表示了应当被删除且返回的元素所在底层列表的索引。
语句self._data[self._front] = None表示此时底层列表的该单元处不再保存期望出队元素对象的索引,此时根据Python的垃圾回收机制:当对象的索引计数降为0时,解释器就会回收该对象。
另外需要注意一点的就是就是dequeue()方法需要在删除队头元素后更新self._front的值,即使得第二个元素成为队头元素,虽然在绝大多数情况下,只需将该值加1即可,但是由于循环使用列表的缘故,队头可能从列表的最后一个单元变为第一个单元,因此需要使用前面提到的取模运算。
c. 倍增底层列表长度
当调用enqueue(e)时恰巧队列元素个数等于底层列表长度,此时就像在【数据结构与算法Python描述】——列表实现原理深入探究及其常用操作时间复杂度分析中的操作一样,可以让列表的长度呈指数级增长,此处为翻倍。
然而,这里需要特别注意的是,在创建长度翻倍的新列表后,在拷贝旧列表中的元素引用至新列表时,此处有意使得队头和新列表索引为0的单元处对齐(如下图所示),这么做并非仅为了美观,而是因为取模运算和列表的长度有关,如果不这么做则会出现问题。
d. 减半底层列表长度
上述代码仍存在的一个缺陷是,最终底层列表的长度和队列中保存过的最多元素数目成正比,而非和当前队列中的元素个数成正比,这可能会造成一定程度的内存浪费。
为了解决上述问题,可以在队列中元素个数小于底层列表长度的 1 / 4 {\left. 1\middle/ 4\right.} 1/4时将底层列表长度减半。
为实现上述算法,我们只需要在dequeue()的代码中加入下列两行代码即可:
if 0 < self._size < len(self._data) // 4:
self._resize(len(self._data) // 2)
即此时dequeue()的完整代码为:
def dequeue(self):
"""
按照FIFO(先进先出)的原则删除并返回队头元素,当队列为空时抛出Empty异常
:return: 队头元素
"""
if self.is_empty():
raise Empty('队列当前为空!')
ans = self._data[self._front]
self._data[self._front] = None # 协助解释器进行GC(Garbage Collection)
self._front = (self._front + 1) % len(self._data) # 将队头所对应列表索引值加1或归零
self._size -= 1
if 0 < self._size < len(self._data) // 4:
self._resize(len(self._data) // 2)
return ans
4.3 队列操作复杂度分析
针对本文使用Python列表所实现的队列各方法,下表给出了其各自的时间复杂度:
- 对于
Q.first()、Q.is_empty()和len(Q):毫无疑问其时间复杂度均为 O ( 1 ) O(1) O(1); - 对于
Q.enqueue(e)和Q.dequeue():类似文章【数据结构与算法Python描述】——列表实现原理深入探究及其常用操作时间复杂度分析中对于列表append()和pop()方法的分析,其 O ( 1 ) O(1) O(1)时间复杂也为摊销后结果。
| 队列操作 | 时间复杂度 |
|---|---|
Q.enqueue(e) |
O ( 1 ) O(1) O(1)1 |
Q.dequeue() |
O ( 1 ) O(1) O(1)1 |
Q.first() |
O ( 1 ) O(1) O(1) |
Q.is_empty() |
O ( 1 ) O(1) O(1) |
len(Q) |
O ( 1 ) O(1) O(1) |
二、双端队列
1. 双端队列的定义
双端队列顾名思义是一种特殊的队列,这种队列除了支持从队尾插入元素、从队头删除元素以外,还支持从队头插入元素、从队尾删除元素,这也是所谓“双端”的含义所在,双端队列一般用英文单词deque来表示。
2. 双端队列的原型
对于双端队列的原型,可以还用排队的例子来说明,这里主要以此说明从队头入队和从队尾出队的例子:
- 如果一个排在队头的顾客进了餐厅却发现暂无空桌,则其再次回到队头的行为就相当于从队头入队操作;
- 如果一个排在队尾的顾客嫌队伍太长离开了队伍,则其行为就相当于从队尾出队操作。
3. 双端队列的ADT
为了能够提供上述双端队列所支持的所有操作,则其ADT必然需要至少包含下列4个方法:
D.add_first(e):在队头插入元素e;D.add_last(e):在队尾插入元素e;D.delete_first():删除并返回队头元素且当双端队列为空时抛出异常;D.delete_last():删除并返回队尾元素且当双端队列为空时抛出异常。
同样地,为了更好地使用双端队列,一般还需定义下列实用方法:
D.first():返回但不删除队头元素,且当双端队列为空时抛出异常;D.last():返回但不删除队尾元素,且当双端队列为空时抛出异常;D.is_empty():当双端队列中没有任何元素时返回True;__len__():重写该方法使其返回当前双端队列元素个数。
4. 双端队列的实现
4.1 循环使用列表实现双端队列
由于双端队列和上述普通队列的相似性,可以在上述ListQueue的基础上实现双端队列ListDeque,此处仍只需要同样的3个实例属性_data,_size以及_front。下面给出了实现上述双端队列ADT的完整代码,其中:
- 对于
D.last(),需要知道当前队尾元素所在底层列表单元的索引值,为此同样可以使用如下取模运算表达式:back = (self._front + self._size − 1) % len(self._data); - 对于
D.first(),该方法的实现和上述普通队列的同名方法实现完全一致; - 对于
D.add_last():该方法的实现和上述普通队列的enqueue()方法实现完全一致; - 对于
D.add_first():实现该方法在绝大多数情况下仅需要将队头的索引减1即可,但需要特别注意的是,有可能此时self._front = 0,如果此时队列元素未满,则需要让元素插入底层数组最右侧单元,此时该单元的索引为(len(self._data) - 1),因此此处也需要使用型如self._front = (self._front - 1) % len(self._data)的取模运算; - 对于
D.delete_last():使用和D.last()中同样的取模运算表达式即可得到队尾元素在底层列表的索引,用此索引使得对应列表单元引用对象None即可; - 对于
D.delete_first():该方法和上述普通队列的dequeue()方法的实现完全一致; - 对于
D.printer:此为使用@property装饰后的一个生成器,用于打印双端队列。
class Empty(Exception):
"""尝试对空队列执行pop()或top()操作时抛出的异常"""
pass
class ListDeque:
"""双端队列实现类,使用Python列表作元素存储用"""
DEFAULT_CAPACITY = 10 # 为新创建双端队列分配的适当大小
def __init__(self):
"""创建新的空队列时的初始化方法"""
self._data = [None] * ListDeque.DEFAULT_CAPACITY
self._size = 0
self._front = 0
def __len__(self):
"""
返回队列中元素个数
:rtype: int
:return: 元素个数
"""
return self._size
def __str__(self):
"""
以无歧义的方式返回栈的字符串表示形式
:rtype: str
:return: 底层列表的字符串表示形式
"""
return str(self._data)
@property
def printer(self):
"""
创建一个双端队列生成器
:return:
"""
if self.is_empty():
raise Empty('队列当前为空!')
i = 0
cursor = self._front
while i < self._size:
if self._data[cursor] is not None:
yield self._data[cursor]
i += 1
cursor = (cursor + 1) % len(self._data)
def is_empty(self):
"""
队列为空时返回True,否则返回False
:rtype: Boolean
:return: 队列是否为空
"""
return self._size == 0
def first(self):
"""
返回但不删除队头元素,当队列为空时抛出Empty异常
:rtype: object
:return: 队头元素
"""
if self.is_empty():
raise Empty('队列当前为空!')
return self._data[self._front]
def last(self):
"""
返回但不删除队尾元素,当队列为空时抛出Empty异常
:rtype: object
:return: 队尾元素
"""
if self.is_empty():
raise Empty('队列当前为空!')
back = (self._front + self._size - 1) % len(self._data)
return self._data[back]
def delete_last(self):
"""
删除并返回队尾元素,当队列为空时抛出Empty异常
:rtype: object
:return: 队尾元素
"""
if self.is_empty():
raise Empty('队列当前为空!')
ans = self.last() # 直接获取队尾元素
# self._data[self._data.index(ans)] = None # 时间的复杂度较高
back = (self._front + self._size - 1) % len(self._data)
self._data[back] = None
self._size -= 1
if 0 < self._size < len(self._data) // 4:
self._resize(len(self._data) // 2)
return ans
def delete_first(self):
"""
删除并返回队头元素,当队列为空时抛出Empty异常
:rtype: object
:return: 队头元素
"""
if self.is_empty():
raise Empty('队列当前为空!')
ans = self._data[self._front]
self._data[self._front] = None # 协助解释器进行GC(Garbage Collection)
self._front = (self._front + 1) % len(self._data) # 将队头所对应列表索引值加1或归零
self._size -= 1
if 0 < self._size < len(self._data) // 4:
self._resize(len(self._data) // 2)
return ans
def add_last(self, e):
"""
向队尾插入一个元素
:param e: 待插入队尾的元素
:return: None
"""
if self._size == len(self._data): # 用于存储队列元素的底层列表是否已满
self._resize(2 * len(self._data)) # 将列表长度翻倍
avail = (self._front + self._size) % len(self._data)
self._data[avail] = e
self._size += 1
def add_first(self, e):
"""
向队头插入一个元素
:param e: 待插入队头的元素
:return: None
"""
if self._size == len(self._data):
self._resize(2 * len(self._data))
self._front = (self._front - 1) % len(self._data)
self._data[self._front] = e
self._size += 1
def _resize(self, capacity):
"""
调整用于存储队列元素的底层列表长度
:param capacity: 期望的列表长度
:return: None
"""
old_lst = self._data # 记录原始列表的引用
self._data = [None] * capacity # 分配新的列表,并将其作为存储队列元素的容器
walk = self._front
for k in range(self._size): # 循环将旧列表元素拷贝至新列表
self._data[k] = old_lst[walk]
walk = (1 + walk) % len(old_lst)
self._front = 0 # 将队头和新列表的第一个单元对齐
def main():
lst_deque = ListDeque()
lst_deque.add_last(5)
print(list(lst_deque.printer)) # [5]
lst_deque.add_first(3)
print(list(lst_deque.printer)) # [3, 5]
lst_deque.add_first(7)
print(list(lst_deque.printer)) # [7, 3, 5]
print(lst_deque.first()) # 7
print(lst_deque.delete_last()) # 5
print(len(lst_deque)) # 2
print(lst_deque.delete_last()) # 3
print(lst_deque.delete_last()) # 7
lst_deque.add_first(6)
print(list(lst_deque.printer)) # [6]
print(lst_deque.last()) # 6
lst_deque.add_first(8)
print(list(lst_deque.printer)) # [8, 6]
print(lst_deque.is_empty()) # False
print(lst_deque.last()) # 6
if __name__ == '__main__':
main()
5. collection模块的deque类
实际上,Python在內置的collections模块中內置了一个双端队列类deque,下面是上述自定义双端队列类ListDeque和collections.deque类的常用方法对比。
ListDeque的ADT |
collections.deque |
功能描述 |
|---|---|---|
len(D) |
len(D) |
获取双端队列元素个数 |
D.add_first() |
D.appendleft() |
在队头插入元素 |
D.add_last() |
D.append() |
在队尾插入元素 |
D.delete_first() |
D.popleft() |
删除队头元素 |
D.delete_last() |
D.pop() |
删除队尾元素 |
D.first() |
D[0] |
获取队头元素 |
D.last() |
D.[-1] |
获取队尾元素 |
D.[j] |
使用索引获取任意位置元素 | |
D.[j] = val |
使用索引修改任意位置元素 | |
D.clear() |
删除队列所有元素 | |
D.rotate(k) |
所有循环平移k个单元2 |
实际上,collections.deque类的初始化方法中还有一个可选参数maxlen,该参数可以强制指定一个固定长度的deque实例,如果在创建双端队列实例时指定了该参数,则当队列此时已满时,调用append()(或appendleft())方法时,会导致底层隐式调用popleft()(或pop())方法,让队列的另一端空出一个单元。
摊销后的时间复杂度。 ↩︎ ↩︎
如果
k为正(负)整数,则队列所有元素向右(左)循环平移k个单元,如D.rotate(1)相当于D.appendleft(D.pop()),D.rotate(-1)相当于D.append(D.popleft())。 ↩︎