【数据结构学习】二叉树的层序生成,非递归遍历(前中后序),递归遍历(c++)
转载请注明出处:https://blog.csdn.net/loiter2/article/details/105047663
【数据结构学习】二叉树的层序生成,非递归遍历(前中后序),递归遍历(c++)
-
- 1、二叉树的层序生成
-
-
- 二叉树结构体和队列结构体构建
- 层序生成二叉树
-
- 2、二叉树的非递归遍历
-
-
- 非递归前序遍历和非递归中序遍历
- 非递归后序遍历
-
- 3、二叉树的递归遍历
- 4、完整代码
【数据结构学习】系列用来记录一下自己在数据结构学习过程中的总结、代码实现等内容。
本篇记录了二叉树的层序生成,非递归遍历(前中后序),递归遍历。其中二叉树的层序生成使用了简单的队列知识,入队和出队;非递归遍历是用到了数组实现的简单堆栈,学到二叉树,这些知识应该基本都已经学到了,即使忘记了,结合注释也比较容易看懂。
1、二叉树的层序生成
二叉树结构体和队列结构体构建
层序生成二叉树的方法需要有个队列暂时存储输入数据,因此除了构建二叉树结构体外,还需要构建队列结构体。
二叉树采用链表存储,队列采用动态数组存储。
typedef int ElementType; //方便更改二叉树节点数据区的数据属性
//------定义二叉树节点------//
typedef struct TNode BinTree;
struct TNode{
ElementType data;
BinTree* left;
BinTree* right;
};
//------定义一个队列------//
typedef struct QNode Queue;
struct QNode{
BinTree** data;
int front, rear;
int maxsize;
};
层序生成二叉树
采用层序生成二叉树的基本思路是:
- 读取输入的第一个数据,判断是否为正常数据,若为正常,则创建为根节点,并让根节点入队;
- 让根节点出队,读取下一个输入数据,判断是否为正常数据,若为正常,则让其成为根节点的左子树,并让该节点入队;若非正常,则左子树为空;
- 继续读取下一个输入数据,判断是否为正常数据,若为正常,则让其成为根节点的右子树,并让该节点入队;若非正常,则右子树为空;
- 接着判断队列是否为空,若不为空,则让下一个节点出队,重复步骤2、3,直到队列为空,则读取完了所有输入数据,构建完毕。
c++代码实现如下:
/*二叉树生成函数中所使用的队列相关的函数:
生成队列,出队,判断队空等,后文均有具体函数构建,
暂时根据名字了解其作用即可*/
BinTree* creatBTree()
{
BinTree* root;
ElementType data;
Queue* Q;
Q = creatQueue(20); //生成队列是采用动态数组的方式,输入参数为队列最大值;
cout<<"请按层序的方法输入二叉树数据,以0代表空节点"<<endl;
cin>>data;
if (data!=nofo) {
//nofo代表输入的为非正常数据,本实现被定义为0
root = new BinTree;
root->data=data;
root->left=root->right=NULL;
addQ(Q, root); //入队函数
}
else return NULL;
while (!isEmpty(Q)){
//判断队空函数
BinTree* T = deleQ(Q); //出队函数
cin>>data;
if (data!=nofo){
T->left = new BinTree;
T->left->data = data;
addQ(Q, T->left);
}else T->left=NULL;
cin>>data;
if (data!=nofo){
T->right = new BinTree;
T->right->data = data;
addQ(Q, T->right);
}else T->right = NULL;
}
return root;
}
注:代码中,每个叶子节点都要两个0要输入,给出一组输入案例,方便输入和理解:1 2 3 4 5 6 7 0 8 0 0 9 10 0 0 0 0 0 0 0 0
该输入案例代表的二叉树为:
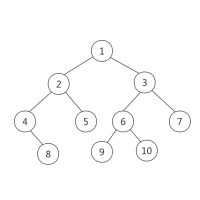
注:该案例来源于别人的博客:【数据结构】层序生成二叉树
(博主对不起,我太懒了,没有自己画,如果冒犯了请联系,我一定删除道歉)
2、二叉树的非递归遍历
二叉树的非递归遍历方法,是使用堆栈实现,本文在代码实现有些偷懒,用了一个固定数组来简单构建了一个堆栈。
要清楚的一点是,不管是前序、中序还是后序,经过二叉树每个节点的顺序都是一致的,只是访问他的先后的问题。如下图,“叉叉”为前序,“星星”为中序,“三角”为后序。
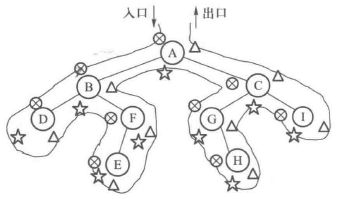
注:图片来自与陈越姥姥著的数据结构课本,顺便安利一下陈越姥姥和何钦铭老师的数据结构慕课,b站有课程视频:b站陈越姥姥数据结构课
非递归前序遍历和非递归中序遍历
非递归前序遍历的基本思路:
- 从根节点开始,遇到某个节点,直接访问(在代码里体现为输出),并且让该节点入栈,之后继而访问其左子树;依次类推,直至左子树为空;
- 让当前节点出栈,访问其右子树,并入栈;
- 不断重复步骤1,2,直至节点为空且栈为空,遍历完成。
中序遍历的思路与前序遍历一致,只是把访问(输出)的操作,放在当前节点出栈时进行,而非入栈时。
非递归前序遍历c++实现:
void PreOrderTraversal(BinTree* root)
{
BinTree* T;
BinTree* stack[20];
int top = -1;
T = root;
while(T||top!=-1){
while(T){
cout<<T->data<<"\t";
stack[++top] = T;
T = T->left;
}
T = stack[top--];
T = T->right;
}
cout<<endl;
}
非递归中序遍历c++实现:
void InOrderTraversal(BinTree* root)
{
BinTree* T;
BinTree* stack[15];
int top = -1;
T = root;
while(T||top!=-1){
while(T){
stack[++top] = T;
T = T->left;
}
T = stack[top--];
cout<<T->data<<"\t";
T = T->right;
}
cout<<endl;
}
从代码也可以看出,只是把输出语句从入栈位置(先序)放到了出栈位置(中序)
非递归后序遍历
为什么要把非递归后序遍历单独拿出来说?因为后序遍历是在第三次遇到某个节点时才将其输出(出栈),输出之前必须要通过该节点先访问其右子树,也即在第二次遇到该节点时应该进行取栈操作。明白这个道理后就简单很多了,只需加一个判断标志,判断是第二次遇到该节点还是第三次遇到该节点即可。(第一次遇到入栈,第二次遇到取栈,第三次遇到出栈)
非递归后序遍历c++实现:
void PostOrderTraversal(BinTree* root)
{
BinTree* T;
BinTree* stack[20];
int top = -1;
int flagstack[20];
T = root;
while(T||top!=-1){
while(T){
stack[++top] = T;
flagstack[top] = 0;
T = T->left;
}
if(flagstack[top] == 0){
T = stack[top];
T = T->right;
flagstack[top] = 1;
}
else{
T = stack[top--];
cout<<T->data<<"\t";
T = NULL; //这步操作很关键,既要保证循环回退到当前节点的父节点,又要保证栈顶元素不变
}
}
}
3、二叉树的递归遍历
二叉树的非递归遍历都会了,递归遍历就相当简单了,只是在递归左右子树的前中后插入输出就行了,这里写出来也只是为了保证这部分内容的完整性。
//这里只写了先序,中序和后序只是把输出换个地方
void RecursiveTraversal(BinTree *BT)
{
if (BT){
cout<<BT->data<<"\t";
RecursiveTraversal(BT->left);
RecursiveTraversal(BT->right);
}
}
4、完整代码
下面是包括了结构体构建、遍历函数的定义、队列函数的定义等等完整代码,可以直接复制粘贴运行的,方便小白的直接使用(啊啊啊,我也是小白,深知有时候只是看到别人一部分代码,自己整合好久还会出错的痛苦,没错,是我太菜了)
#include