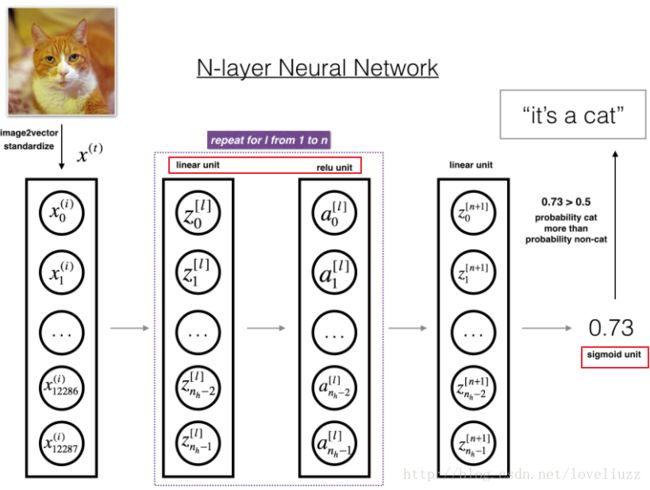
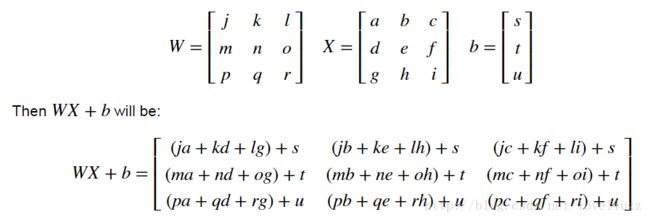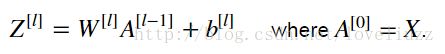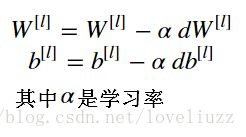DNN案例——一步步构建深层神经网络
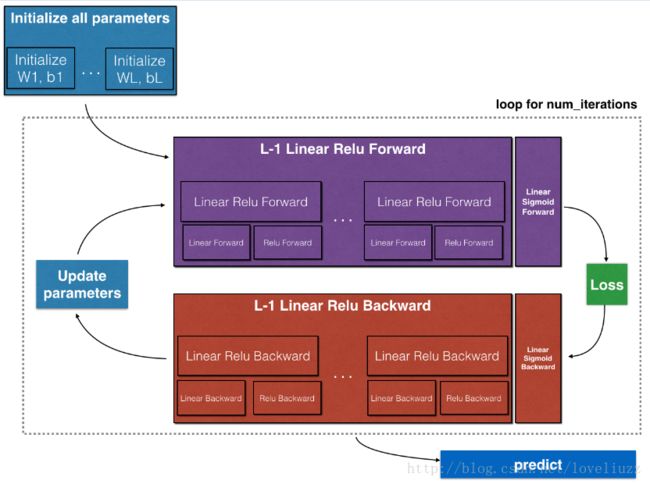
一、总体目标与大致结构
构建一个深层神经网络,该深层神经网络拥有任意想要的多个层。
(1)采用像ReLU这样的非线性单元来增强模型。
(2)构建一个通用的多于一个隐藏层的深层神经网络。
(3)利用构建的深层神经网络进行图片的分类。
注意:
二、应用的包import
1、numpy是Python的科学计算的基础包。
2、h5py 是一种常见的封装和数据集存储在H5交互文件。python开源库——h5py快速指南,数据集dataset ("data.h5"),详细见链接:http://blog.csdn.net/yudf2010/article/details/50353292
3、matplotlib是python中著名的绘图工具包。
4、scipy:操控numpy数组的高级科学计算库,详细scipy简介见链接:
http://blog.csdn.net/q583501947/article/details/76735870
scipy中ndimage模块是有关数学形态学,详细链接见:http://blog.csdn.net/SHU15121856/article/details/76349846
5、PIL:python图像处理库,详细介绍见链接:http://blog.csdn.net/icamera0/article/details/50651926
Image模块是PIL中最重要的模块,它提供了诸多图像操作的功能,比如创建、打开、显示、保存图像等功能,合成、裁剪、滤波等功能,获取图像属性功能,如图像直方图、通道数等。
4、dnn_utils_v2.py文件:定义一些必要的函数,sigmoid函数、ReLU函数等激活函数,具体代码如下:
#!/usr/bin/env python
# -*- coding:utf-8 -*-
# Author:ZhengzhengLiu
import numpy as np
#sigmoid激活函数
def sigmoid(Z):
"""
param :
Z: 任意维度的numpy数组
return:
A -- sigmoid(Z)的输出,与Z的维度相同
cache -- 返回Z,存储起来在反向传播时使用
"""
A = 1/(1+np.exp(-Z))
cache = Z
return A,cache
# ReLU激活函数
def relu(Z):
"""
param :
Z -- 任意维度,线性层的输出
return:
A -- 激活后的结果, 与Z的维度相同
cache -- python字典包含"A" ,存储起来以便高效执行反向传播
"""
A = np.maximum(0,Z)
# Python中的assert断言用起来非常简单,可在assert后面跟上任意判断条件
# 如果断言失败则会抛出异常
assert (A.shape == Z.shape)
cache = Z
return A,cache
#利用ReLU单元计算反向传播
def relu_backward(dA,cache):
"""
param :
dA -- 任意维度,损失函数对A的梯度
cache -- Z,存储起来在反向传播时使用
return:
dZ -- 损失函数对Z的梯度 = 损失函数对A的梯度 * relu激活函数对Z的梯度
"""
Z = cache
dZ = np.array(dA,copy=True) #relu激活函数在Z>0时梯度为1
#当Z<=0时,将dZ设置为0
dZ[Z <= 0] = 0
assert (dZ.shape == Z.shape)
return dZ
#利用sigmoid单元计算反向传播
def sigmoid_baakward(dA,cache):
"""
param :
dA -- 任意维度,损失函数对A的梯度
cache -- Z,存储起来在反向传播时使用
return:
dZ -- 损失函数对Z的梯度 = 损失函数对A的梯度 * sigmoid激活函数对Z的梯度
"""
Z = cache
s = 1/(1+np.exp(-Z))
dZ = dA * s * (1 - s)
assert (dZ.shape == Z.shape)
return dZ5、testCases_v2.py文件:定义一些测试函数
三、深层神经网络
(一)架构
1、初始化两层神经网络和L层神经网络的参数
2、执行正向传播模块
3、计算损失函数
4、执行反向传播模块
5、更新参数
(二)两层神经网络与多层神经网络——初始化参数
2.1、两层神经网络——初始化参数
(5)存储每层的神经单元数目,用n加上上标[l]表示,存储在一个列表类型的变量layer_dims中,假设layer_dims对每层的神经单元数目为:[2,4,1],则:W1维度为: (4,2), b1维度为:(4,1), W2维度为:(1,4),b2 维度为(1,1).
(三)两层神经网络与多层神经网络——前向传播模块
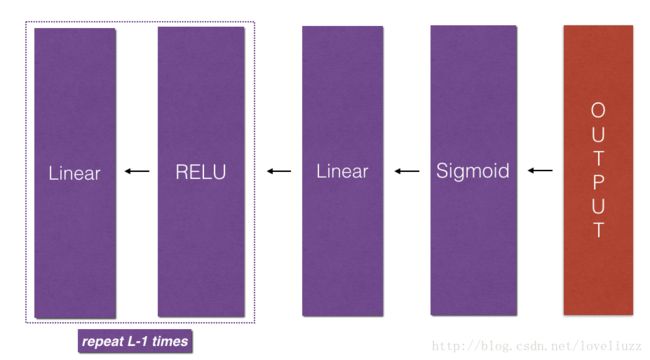
分为三个部分,分别为:线性部分、线性--激活部分、L-1次线性--rReLU+线性--sigmoid(整体前向传播部分)
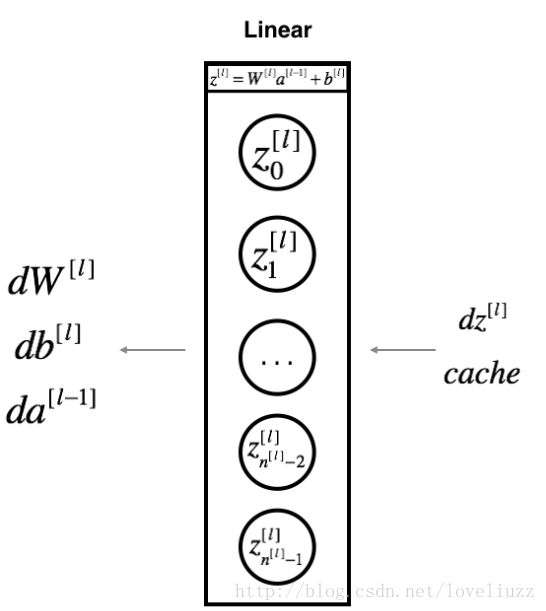
3.1 前向传播——线性部分
使用的公式如下:
注意:上面公式中,使用np.dot()非常有用。
3.2前向传播——线性--激活部分
激活函数有两种,分别为:ReLU和sigmoid函数
(1)sigmoid函数
该函数返回两个值:分别是激活值 A 以及缓存值cache(包含Z,在反向传播时用到),表示如下:
(2)ReLU函数
该函数也返回两个值:分别是激活值 A 以及缓存值cache(包含Z,在反向传播时用到),表示如下:
(3)将 线性Linear 与 激活Activation 进行合并,得到LINEAR->ACTIVATION部分,即:先执行前向传播线性部分,再执行前向传播激活部分。
举例:构建每层前向传播的LINEAR->ACTIVATION部分,采用线性部分以及相应的激活部分,公式如下:
注意:这里的 g 可以是ReLU函数,也可以是sigmoid函数。
3.3前向传播——L-1次线性--ReLU+线性--sigmoid(整体L层前向传播)
深层神经网络(L层)需要L−1次使用relu作为激活函数的前向传播(linear_activation_forward with RELU)
接着 跟上一次sigmoid作为激活函数的前向传播(linear_activation_forward with SIGMOID.)
用变量AL计算下面公式:
注意:利用for循环来计算 L-1 次的[LINEAR->RELU] ,将每次的缓存cache循环加入到事先定义好的caches列表中
利用输入X和整体的前向传播过程,输出一个行向量AL,它是经过前向传播计算的预测值,利用它可以计算损失函数,另外,在caches列表中缓存了所有的中间值。
(四)两层神经网络与多层神经网络——损失函数
利用交叉熵来计算目标函数cost J,应用的公式如下:
知识点:
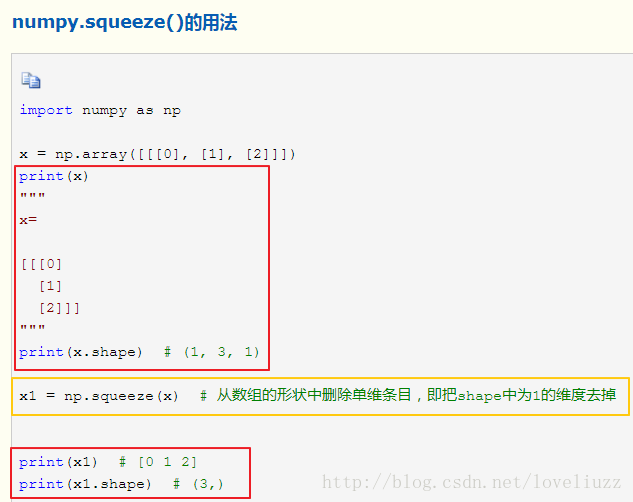
1、keepdims
2、np.squeeze()——从数组中删除单维条目,即:把shape中的一维维度去掉
3、np.asarray()
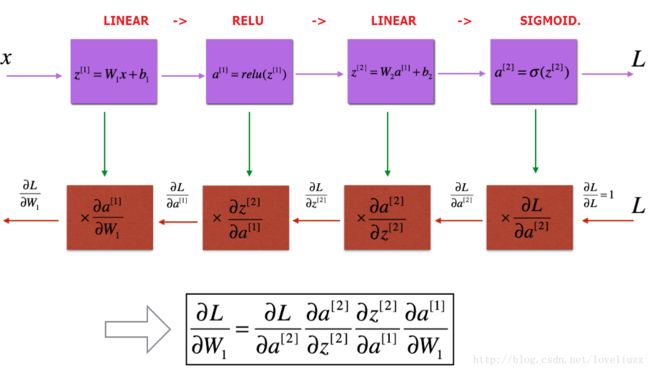
(五)两层神经网络与多层神经网络——反向传播模块
反向传播被用来计算损失函数相对于参数的梯度,反向传播计算与前向传播类似,也分为三部分:
线性部分、线性--激活部分、L-1次线性--ReLU+线性--sigmoid(整体反向传播部分)
5.1、反向传播——线性部分
对神经网络的第l层,线性的前向传播计算公式如下:
后边紧接着一个激活函数,假设你已经计算了导数dZ[l]
根据输入导数dZ[l]则可以通过反向传播计算得到输出 :![]() ,计算公式如下:
,计算公式如下:
5.2、反向传播——线性--激活部分
利用函数linear_activation_backward将函数linear_backward和对激活函数的反向传播合并到一起。提供两个反向传播的函数,分别是:sigmoid_backward和relu_backward。
(1)sigmoid_backward:对sigmoid单元执行反向传播。可以如下定义:
(2)relu_backward:对relu单元执行反向传播。可以如下定义:
如果激活函数用g(.)表示,sigmoid_backward和relu_backward的计算如下:
5.3、反向传播——L层深层神经网络整体的反向传播
在 深层神经网络整体前向传播函数L_model_forward中,每次迭代存储了一个cache缓存包含(X,W,b, 和 Z)
在反向传播过程中利用这些缓存的参数来计算梯度。在L_model_backward函数中,从第L层开始然后依次对所有
1、初始化反向传播
对深层神经网络进行反向传播计算,我们知道输出为:
代码中需要计算dAL:
初始化反向传播的公式如下:
2、反向传播计算
可利用目标函数cost对A[L]的梯度值进行反向传播,将dAL喂给 LINEAR->SIGMOID反向传播函数,
这里用到
函数对其他层进行迭代,应该存储每一个dA, dW和 db在 grads字典中,如下所示:
举例:对于l=3,![]() 存储在grads["dW3"]。
存储在grads["dW3"]。
(六)两层神经网络与多层神经网络——参数更新
函数update_parameters() 应用梯度下降法进行参数更新,更新后的参数存储在字典parameters 中,
![]()
公式如下:
(六)代码
1、test_cases_v2.py测试文件的代码:
#!/usr/bin/env python
# -*- coding:utf-8 -*-
# Author:ZhengzhengLiu
import numpy as np
def linear_forward_test_case():
np.random.seed(1)
A = np.random.randn(3,2)
W = np.random.randn(1,3)
b = np.random.randn(1,1)
return A,W,b
def linear_activation_forward_test_case():
np.random.seed(2)
A_prev = np.random.randn(3,2)
W = np.random.randn(1,3)
b = np.random.randn(1,1)
return A_prev,W,b
def L_model_forward_test_case():
np.random.seed(1)
X = np.random.randn(4,2)
W1 = np.random.randn(3,4)
b1 = np.random.randn(3,1)
W2 = np.random.randn(1,3)
b2 = np.random.randn(1,1)
parameters = {"W1":W1,"b1":b1,"W2":W2,"b2":b2}
return X,parameters
def compute_cost_test_case():
Y = np.asarray([[1,1,1]])
AL = np.asarray([[.8,.9,0.4]])
return Y,AL
def linear_backward_test_case():
np.random.seed(1)
dZ = np.random.randn(1,2)
A = np.random.randn(3,2)
W = np.random.randn(1,3)
b = np.random.randn(1,1)
linear_cache = (A,W,b)
return dZ,linear_cache
def linear_activation_backward_test_case():
np.random.seed(2)
dA = np.random.randn(1,2)
A = np.random.randn(3,2)
W = np.random.randn(1,3)
b = np.random.randn(1,1)
Z = np.random.randn(1,2)
linear_cache = (A,W,b)
activation_cache = Z
linear_activation_cache = (linear_cache,activation_cache)
return dA,linear_activation_cache
def L_model_backward_test_case():
np.random.seed(3)
AL = np.random.randn(1,2)
Y = np.array([[1,0]])
A1 = np.random.randn(4,2)
W1 = np.random.randn(3,4)
b1 = np.random.randn(3,1)
Z1 = np.random.randn(3,2)
linear_cache_activation_1 = ((A1,W1,b1),Z1)
A2 = np.random.randn(3, 2)
W2 = np.random.randn(1, 3)
b2 = np.random.randn(1, 1)
Z2 = np.random.randn(1, 2)
linear_cache_activation_2 = ((A2, W2, b2), Z2)
caches = (linear_cache_activation_1,linear_cache_activation_2)
return AL,Y,caches
def update_parameters_test_case():
np.random.seed(2)
W1 = np.random.randn(3,4)
b1 = np.random.randn(3,1)
W2 = np.random.randn(1,3)
b2 = np.random.randn(1,1)
parameters = {"W1":W1,"b1":b1,"W2":W2,"b2":b2}
np.random.seed(3)
dW1 = np.random.randn(3, 4)
db1 = np.random.randn(3, 1)
dW2 = np.random.randn(1, 3)
db2 = np.random.randn(1, 1)
grads = {"dW1": dW1, "db1": db1, "dW2": dW2, "db2": db2}
return parameters,grads
#!/usr/bin/env python
# -*- coding:utf-8 -*-
# Author:ZhengzhengLiu
#构建任意层的深层神经网络
import numpy as np
import h5py
import matplotlib.pyplot as plt
from dnn_utils_v2 import sigmoid,relu,relu_backward,sigmoid_backward
from test_cases_v2 import *
#架构
"""
1、初始化两层神经网络和L层神经网络的参数
2、执行正向传播模块,
第一层到第L-1层执行[LINEAR->RELU] 前向函数,第L层执行 [LINEAR->SIGMOID] 前向函数
3、计算损失函数
4、执行反向传播模块,
5、更新参数
"""
#两层神经网络——参数初始化
def initialize_parameters(n_x,n_h,n_y):
"""
param :
n_x -- 输入层大小(节点数目)
n_h -- 隐藏层大小(节点数目)
n_y -- 输出层大小(节点数目)
return:
parameters -- 以python字典形式保存参数
w1 -- 权重矩阵,维度为(n_h,n_x)
b1 -- 偏向向量,维度为(n_h,1)
w2 -- 权重矩阵,维度为(n_y,n_h)
b2 -- 偏向向量,维度为(n_y,1)
"""
np.random.seed(1)
W1 = np.random.randn(n_h,n_x)*0.01
b1 = np.zeros((n_h,1))
W2 = np.random.randn(n_y,n_h)*0.01
b2 = np.zeros((n_y,1))
assert (W1.shape == (n_h,n_x))
assert (b1.shape == (n_h,1))
assert (W2.shape == (n_y,n_h))
assert (b2.shape == (n_y,1))
parameters = {
"W1":W1,
"b1":b1,
"W2":W2,
"b2":b2
}
return parameters
parameters = initialize_parameters(3,2,1)
print("W1="+str(parameters["W1"]))
print("b1="+str(parameters["b1"]))
print("W2="+str(parameters["W2"]))
print("b2="+str(parameters["b2"]))
#L层神经网络——参数初始化
def initialize_parameters_deep(layer_dims):
"""
param :
layer_dims -- python列表,包含每一层的神经单元数目
return:
parameters -- python字典保存参数 W1", "b1", ..., "WL", "bL"
Wl -- weight matrix of shape (layer_dims[l], layer_dims[l-1])
bl -- bias vector of shape (layer_dims[l], 1)
"""
np.random.seed(3)
parameters = {}
L = len(layer_dims) #输出神经网络的层数L
for l in range(1,L):
parameters["W"+str(l)] = np.random.randn(layer_dims[l],layer_dims[l-1])*0.01
parameters["b"+str(l)] = np.zeros((layer_dims[l],1))
assert (parameters["W"+str(l)].shape == (layer_dims[l],layer_dims[l-1]))
assert (parameters["b"+str(l)].shape == (layer_dims[l],1))
return parameters
parameters = initialize_parameters_deep([5,4,3])
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
#正向传播模块——线性部分
def linear_forward(A,W,b):
"""
每层前向传播的线性部分 Z[l]=W[l]A[l-1]+b[l]
param :
A -- 前一层的激活值或输入数据,维度为(前一层神经单元数目n[l-1],样本数目m)
W -- 权重矩阵,维度为(当前层神经单元数目n[l],前一层神经单元数目n[l-1])
b -- 偏向向量,维度为(当前层神经单元数目n[l],1)
return:
Z -- 激活函数的输入值,也叫pre-activation参数
cache -- python字典,包含"A", "W" ,"b",存储为了计算反向传播
"""
Z = np.dot(W,A)+b
assert (Z.shape == (W.shape[0],A.shape[1]))
cache = (A,W,b)
return Z,cache
#测试
A,W,b = linear_forward_test_case() #A,W,b定义的维度见:test_cases_v2.py文件
Z,linear_cache = linear_forward(A,W,b)
print("Z="+str(Z))
#正向传播模块——线性+激活部分
def linear_activation_forward(A_prev,W,b,activation):
"""
计算前向传播每层的LINEAR->ACTIVATION部分
param :
A_prev -- 前一层的激活值或输入数据,维度为(前一层神经单元数目n[l-1],样本数目m)
W -- 权重矩阵,维度为(当前层神经单元数目n[l],前一层神经单元数目n[l-1])
b -- 偏向向量,维度为(当前层神经单元数目n[l],1)
activation -- 当前层的激活值,存储为文本字符串sigmoid"或"relu"
return :
A -- 激活函数的输入值,也叫pre-activation参数
cache -- python字典,包含"linear_cache" 和"activation_cache",存储为了计算反向传播
"""
if activation == "sigmoid":
Z,linear_cache = linear_forward(A_prev,W,b)
A,activation_cache = sigmoid(Z)
elif activation == "relu":
Z, linear_cache = linear_forward(A_prev, W, b)
A,activation_cache = relu(Z)
assert (A.shape == (W.shape[0],A_prev.shape[1]))
cache = (linear_cache,activation_cache)
return (A,cache)
#测试
A_prev,W,b = linear_activation_forward_test_case()
A,linear_activation_cache = linear_activation_forward(A_prev,W,b,activation="sigmoid")
print("With sigmoid: A = "+str(A))
A,linear_activation_cache = linear_activation_forward(A_prev,W,b,activation="relu")
print("With relu: A = "+str(A))
#L层神经网络前向传播
def L_model_forward(X,paramerters):
"""
正向传播 [LINEAR->RELU]*(L-1)->LINEAR->SIGMOID
param :
X -- 数据,numpy数组,维度为(输入大小,样本数目)
paramerters -- 上面函数initialize_parameters_deep()的输出值
return:
AL -- 最后的激活输出值(last post-activation value)
caches -- caches缓存列表,包括如下:
L-1个 linear_relu_forward()函数的cache缓存,下标为:0 至 L-2
1个 linear_sigmoid_forward()函数的cache缓存,下标为:L-1
"""
caches = []
A = X
# " / "就一定表示 浮点数除法,返回浮点结果;" // "表示整数除法
L = len(parameters) // 2 #parameters存储每一层的W和b,除以2得到深度网络的层数
#执行(L-1)次[LINEAR->RELU],并将每次的cache缓存添加到caches列表中
for l in range(1,L):
A_prev = A
W = parameters["W"+str(l)]
b = parameters["b"+str(l)]
A, cache = linear_activation_forward(A_prev,W,b,"relu")
caches.append(cache)
#执行1次LINEAR -> SIGMOID,并将cache缓存添加到caches列表中
W = parameters["W"+str(L)]
b = parameters["b"+str(L)]
AL,cache = linear_activation_forward(A,W,b,"sigmoid")
caches.append(cache)
assert (AL.shape == (1,X.shape[1])) # 1 代表最后一层神经单元的个数为 1 个
return AL,caches
#测试
X,parameters = L_model_forward_test_case()
AL,caches = L_model_forward(X,parameters)
print("AL="+str(AL))
print("Length of caches list ="+str(len(caches)))
#计算损失函数
def compute_cost(AL,Y):
"""
param :
AL -- 与标签预测相关的向量,维度为:(1,样本数目)
Y -- 标签的真实值,举例:图片中是猫值为1,不是猫值为0,维度为:(1,样本数目)
return:
cost -- 交叉熵成本
"""
m = Y.shape[1] #样本个数
cost = -np.sum(Y * np.log(AL) + (1-Y)*np.log(1-AL),axis=1,keepdims=True)/m
cost = np.squeeze(cost) #让cost的维度是我们想要的,如转换[[17]]为17
assert (cost.shape == ())
return cost
#测试
Y,AL = compute_cost_test_case()
cost = compute_cost(AL,Y)
print("cost="+str(cost))
#反向传播——线性部分
def linear_backward(dZ,cache):
"""
实现单层反向传播的线性部分(l层)
param :
dZ -- 关于当前层L的线性输出Z的成本函数的梯度
cache -- 当前层前向传播的元组的值(a_prev,W,b)
return:
dA_prev -- 成本函数对前一层第l-1层的激活值的梯度,维度为:与A_prev相同
dW -- 成本函数对当前层第l层的W值的梯度,维度为:与W相同
db -- 成本函数对当前层第l层的b值的梯度,维度为:与b相同
"""
A_prev,W,b = cache
m = A_prev.shape[1] #样本数目
dW = np.dot(dZ,A_prev.T)/m
db = np.sum(dZ,axis=1,keepdims=True)/m
dA_prev = np.dot(W.T,dZ)
assert (dA_prev.shape == A_prev.shape)
assert (dW.shape == W.shape)
assert (db.shape == b.shape)
return dA_prev,dW,db
#测试
dZ,linear_cache = linear_backward_test_case()
dA_prev,dW,db = linear_backward(dZ,linear_cache)
print("dA_prev="+str(dA_prev))
print("dW="+str(dW))
print("db="+str(db))
#反向传播——线性--激活部分
def linear_activation_backward(dA,cache,activation):
"""
对LINEAR->ACTIVATION层执行反向传播
param :
dA -- 对当前层(l层)激活值的梯度
cache -- 元祖值(linear_cache, activation_cache),存储起来方便后续反向传播计算
activation -- 当前层用到的激活函数,以文本字符串存储,为"sigmoid"或"relu"
return:
dA_prev -- 成本函数对前一层第l-1层的激活值的梯度,维度为:与A_prev相同
dW -- 成本函数对当前层第l层的W值的梯度,维度为:与W相同
db -- 成本函数对当前层第l层的b值的梯度,维度为:与b相同
"""
linear_cache, activation_cache = cache
if activation == "relu":
dZ = relu_backward(dA,activation_cache)
dA_prev, dW, db = linear_backward(dZ,linear_cache)
elif activation == "sigmoid":
dZ = sigmoid_backward(dA,activation_cache)
dA_prev, dW, db = linear_backward(dZ,linear_cache)
return dA_prev,dW,db
#测试
AL,linear_activation_cache = linear_activation_backward_test_case()
dA_prev,dW,db = linear_activation_backward(AL,linear_activation_cache,"sigmoid")
print("sigmoid:")
print("dA_prev="+str(dA_prev))
print("dW="+str(dW))
print("db="+str(db))
dA_prev,dW,db = linear_activation_backward(AL,linear_activation_cache,"relu")
print("relu:")
print("dA_prev="+str(dA_prev))
print("dW="+str(dW))
print("db="+str(db))
##反向传播——L层深层神经网络整体部分
def L_model_backward(AL,Y,caches):
"""
对[LINEAR->RELU] * (L-1) -> LINEAR -> SIGMOID计算反向传播
param :
AL -- 预测值构成的向量,正向传播函数L_model_forward()的输出值
Y -- 包含真实标签值的向量(0 if non-cat, 1 if cat)
cache --caches缓存列表,包括如下:
L-1个 linear_relu_forward()函数的cache缓存,下标为:0 至 L-2
1个 linear_sigmoid_forward()函数的cache缓存,下标为:L-1
return:
grads -- 关于梯度的字典
grads["dA" + str(l)] = ...
grads["dW" + str(l)] = ...
grads["db" + str(l)] = ...
"""
grads = {}
L = len(caches) #深层神经网络的层数
m = AL.shape[1] #样本数目
Y = Y.reshape(AL.shape) #Y与AL的维度相同
#反向传播初始化
dAL = -(np.divide(Y,AL) - np.divide(1 - Y,1 - AL))
#第L层(SIGMOID -> LINEAR)的梯度,
# 输入: "AL, Y, caches". 输出: "grads["dAL"], grads["dWL"], grads["dbL"]
current_cache = caches[L-1] #最后一层对应最后一个缓存
grads["dA"+str(L)],grads["dW"+str(L)],grads["db"+str(L)] = linear_activation_backward(dAL,current_cache,"sigmoid")
for l in reversed(range(L-1)):
#第l层:(RELU -> LINEAR)的梯度
#输入:grads["dA" + str(l + 2)], caches. 输出:grads["dA"+str(l+1), grads["dW"+str(l+1)] , grads["db"+str(l+1)]
current_cache = caches[l]
dA_prev_temp,dW_temp,db_temp = linear_activation_backward(grads["dA"+str(l+2)],current_cache,"relu")
grads["dA"+str(l+1)] = dA_prev_temp
grads["dW"+str(l+1)] = dW_temp
grads["db"+str(l+1)] = db_temp
return grads
#测试
AL,Y,caches = L_model_backward_test_case()
print("AL:"+str(AL))
print("Y:"+str(Y))
print("caches:"+str(caches))
grads = L_model_backward(AL,Y,caches)
print("dW1="+str(grads["dW1"]))
print("db1="+str(grads["db1"]))
print("dW2="+str(grads["dW2"]))
print("db2="+str(grads["db2"]))
#更新参数
def update_parameters(parameters,grads,learning_rate):
"""
利用梯度下降更新参数
param :
parameters -- python字典形式的参数
grads -- python字典形式保存的梯度,L_model_backward函数的输出
learning_rate -- 学习率
return:
parameters -- python字典形式的更新后的参数
parameters["W" + str(l)] = ...
parameters["b" + str(l)] = ...
"""
L = len(parameters) // 2 #深层神经网络的层数
#利用for循环执行每个参数的更新
for l in range(L):
parameters["W"+str(l+1)] = parameters["W"+str(l+1)] - learning_rate * grads["dW"+str(l+1)]
parameters["b"+str(l+1)] = parameters["b"+str(l+1)] - learning_rate * grads["db"+str(l+1)]
return parameters
#测试
parameters,grads = update_parameters_test_case()
parameters = update_parameters(parameters,grads,0.1)
print("W1="+str(parameters["W1"]))
print("b1="+str(parameters["b1"]))
print("W2="+str(parameters["W2"]))
print("b2="+str(parameters["b2"]))(一) 数据集简介dataset——"data.h5"
1、训练集:m_train 张被标记的图片,是猫的标签为 1,不是猫的标签为:0
2、测试集:m_test 张被标记的图片,是猫的标签为 1,不是猫的标签为:0
3、每一张图片的大小为 (num_px,num_px,3),其中的 表示RGB三个图像的通道
加载数据集的代码存放在文件 lr_utils.py中,如下所示:
#!/usr/bin/env python
# -*- coding:utf-8 -*-
# Author:ZhengzhengLiu
import numpy as np
import h5py
def load_dataset():
train_dataset = h5py.File('cat_datasets/train_catvnoncat.h5', "r")
train_set_x_orig = np.array(train_dataset["train_set_x"][:]) # your train set features
train_set_y_orig = np.array(train_dataset["train_set_y"][:]) # your train set labels
test_dataset = h5py.File('cat_datasets/test_catvnoncat.h5', "r")
test_set_x_orig = np.array(test_dataset["test_set_x"][:]) # your test set features
test_set_y_orig = np.array(test_dataset["test_set_y"][:]) # your test set labels
classes = np.array(test_dataset["list_classes"][:]) # the list of classes
train_set_y_orig = train_set_y_orig.reshape((1, train_set_y_orig.shape[0]))
test_set_y_orig = test_set_y_orig.reshape((1, test_set_y_orig.shape[0]))
return train_set_x_orig, train_set_y_orig, test_set_x_orig, test_set_y_orig, classestrain_set_x_orig 的 维度大小为:(209,64,64,3),数据类型为:numpy.ndarray
test_set_x_orig 的 维度大小为:(50,64,64,3),train_set_y_orig 的 维度大小为:(1,209)
(二)对数据集的预处理
1、图片变形的向量化处理
12288等于64*64*3的图片变形后的图向量。
2、对图片进行标准化
使得特征值在0--1之间,像素值除以255实现标准化。
(三)模型构建
构建一个深层神经网络实现对数据集的是否是猫的图片进行分类的功能。
分别构建一个两层神经网络和一个L层深层神经网络,比较这些模型的表现,尝试不同的网络层数L比较性能。
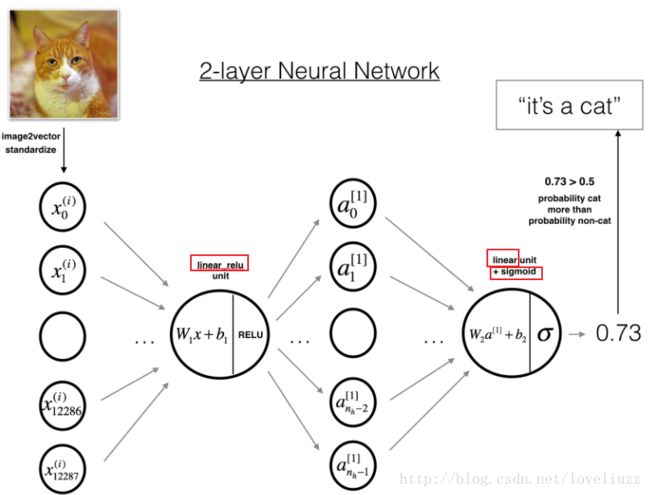
1、两层神经网络
可以总结为:INPUT -> LINEAR -> RELU -> LINEAR -> SIGMOID -> OUTPUT
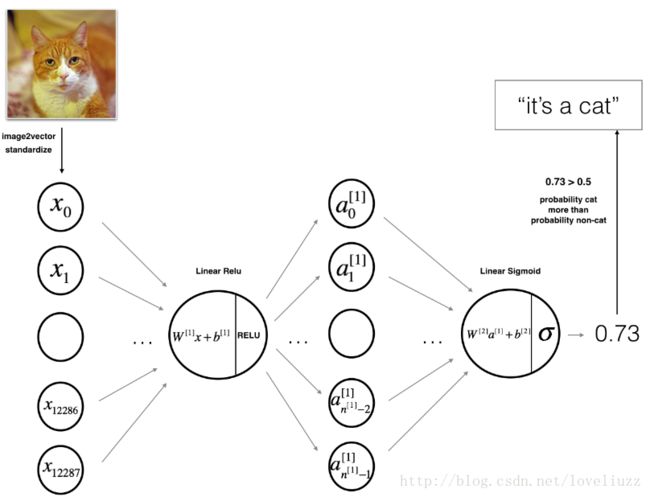
(1)输入图片是(64,64,3)大小的,经过图向量化拉伸后,大小变为:(12288,1)
重复上述步骤,用权重矩阵![]() 乘以上述结果,加上偏向经过sigmoid激活函数得到最终结果。
乘以上述结果,加上偏向经过sigmoid激活函数得到最终结果。
(3)如果,结果大于0.5则分类结果为:是猫。
2、L层深层神经网络
可以总结为:INPUT ->[LINEAR -> RELU] × (L-1) -> LINEAR -> SIGMOID -> OUTPUT
(1)输入图片是(64,64,3)大小的,经过图向量化拉伸后,大小变为:(12288,1)
接着加上一个偏向![]() ,结果被称作 线性部分,对线性部分进行RELU激活函数。
,结果被称作 线性部分,对线性部分进行RELU激活函数。
重复上述步骤,对每一个![]() 执行上述操作,最后对最终得到的线性部分用sigmoid激活函数。
执行上述操作,最后对最终得到的线性部分用sigmoid激活函数。
(3)如果结果大于0.5,则分类结果为:是猫。
3、总结通常构建深层神经网络的方法如下:
(1)初始化参数,定义超参数
(2)num次循环迭代下面的步骤:
a、前向传播
b、计算目标cost函数
c、反向传播
d、利用参数和反向传播的梯度更新参数
(3)利用训练的模型参数来预测分类标签的结果
(四)两层神经网络模型构建
1、结构顺序为:LINEAR -> RELU -> LINEAR -> SIGMOID
2、应用前面构建的函数如下:
这些函数存放在文件名为:dnn_utils_v2.py的文件中,具体代码如下:
#!/usr/bin/env python
# -*- coding:utf-8 -*-
# Author:ZhengzhengLiu
import numpy as np
import h5py
import matplotlib.pyplot as plt
from dnn_utils_v2 import sigmoid,relu,relu_backward,sigmoid_backward
from test_cases_v2 import *
#架构
"""
1、初始化两层神经网络和L层神经网络的参数
2、执行正向传播模块,
第一层到第L-1层执行[LINEAR->RELU] 前向函数,第L层执行 [LINEAR->SIGMOID] 前向函数
3、计算损失函数
4、执行反向传播模块,
5、更新参数
"""
#两层神经网络——参数初始化
def initialize_parameters(n_x,n_h,n_y):
"""
param :
n_x -- 输入层大小(节点数目)
n_h -- 隐藏层大小(节点数目)
n_y -- 输出层大小(节点数目)
return:
parameters -- 以python字典形式保存参数
w1 -- 权重矩阵,维度为(n_h,n_x)
b1 -- 偏向向量,维度为(n_h,1)
w2 -- 权重矩阵,维度为(n_y,n_h)
b2 -- 偏向向量,维度为(n_y,1)
"""
np.random.seed(1)
W1 = np.random.randn(n_h,n_x)*0.01
b1 = np.zeros((n_h,1))
W2 = np.random.randn(n_y,n_h)*0.01
b2 = np.zeros((n_y,1))
assert (W1.shape == (n_h,n_x))
assert (b1.shape == (n_h,1))
assert (W2.shape == (n_y,n_h))
assert (b2.shape == (n_y,1))
parameters = {
"W1":W1,
"b1":b1,
"W2":W2,
"b2":b2
}
return parameters
#L层神经网络——参数初始化
def initialize_parameters_deep(layer_dims):
"""
param :
layer_dims -- python列表,包含每一层的神经单元数目
return:
parameters -- python字典保存参数 W1", "b1", ..., "WL", "bL"
Wl -- weight matrix of shape (layer_dims[l], layer_dims[l-1])
bl -- bias vector of shape (layer_dims[l], 1)
"""
np.random.seed(1)
parameters = {}
L = len(layer_dims) #输出神经网络的层数L
for l in range(1,L):
parameters["W"+str(l)] = np.random.randn(layer_dims[l],layer_dims[l-1])/np.sqrt(layer_dims[l-1])#*0.01
parameters["b"+str(l)] = np.zeros((layer_dims[l],1))
assert (parameters["W"+str(l)].shape == (layer_dims[l],layer_dims[l-1]))
assert (parameters["b"+str(l)].shape == (layer_dims[l],1))
return parameters
#正向传播模块——线性部分
def linear_forward(A,W,b):
"""
每层前向传播的线性部分 Z[l]=W[l]A[l-1]+b[l]
param :
A -- 前一层的激活值或输入数据,维度为(前一层神经单元数目n[l-1],样本数目m)
W -- 权重矩阵,维度为(当前层神经单元数目n[l],前一层神经单元数目n[l-1])
b -- 偏向向量,维度为(当前层神经单元数目n[l],1)
return:
Z -- 激活函数的输入值,也叫pre-activation参数
cache -- python字典,包含"A", "W" ,"b",存储为了计算反向传播
"""
Z = np.dot(W,A)+b
assert (Z.shape == (W.shape[0],A.shape[1]))
cache = (A,W,b)
return Z,cache
#正向传播模块——线性+激活部分
def linear_activation_forward(A_prev,W,b,activation):
"""
计算前向传播每层的LINEAR->ACTIVATION部分
param :
A_prev -- 前一层的激活值或输入数据,维度为(前一层神经单元数目n[l-1],样本数目m)
W -- 权重矩阵,维度为(当前层神经单元数目n[l],前一层神经单元数目n[l-1])
b -- 偏向向量,维度为(当前层神经单元数目n[l],1)
activation -- 当前层的激活值,存储为文本字符串sigmoid"或"relu"
return :
A -- 激活函数的输入值,也叫pre-activation参数
cache -- python字典,包含"linear_cache" 和"activation_cache",存储为了计算反向传播
"""
if activation == "sigmoid":
Z,linear_cache = linear_forward(A_prev,W,b)
A,activation_cache = sigmoid(Z)
elif activation == "relu":
Z, linear_cache = linear_forward(A_prev, W, b)
A,activation_cache = relu(Z)
assert (A.shape == (W.shape[0],A_prev.shape[1]))
cache = (linear_cache,activation_cache)
return (A,cache)
#L层神经网络前向传播
def L_model_forward(X,parameters):
"""
正向传播 [LINEAR->RELU]*(L-1)->LINEAR->SIGMOID
param :
X -- 数据,numpy数组,维度为(输入大小,样本数目)
parameters -- 上面函数initialize_parameters_deep()的输出值
return:
AL -- 最后的激活输出值(last post-activation value)
caches -- caches缓存列表,包括如下:
L-1个 linear_relu_forward()函数的cache缓存,下标为:0 至 L-2
1个 linear_sigmoid_forward()函数的cache缓存,下标为:L-1
"""
caches = []
A = X
# " / "就一定表示 浮点数除法,返回浮点结果;" // "表示整数除法
L = len(parameters) // 2 #parameters存储每一层的W和b,除以2得到深度网络的层数
#执行(L-1)次[LINEAR->RELU],并将每次的cache缓存添加到caches列表中
for l in range(1,L):
A_prev = A
W = parameters["W"+str(l)]
b = parameters["b"+str(l)]
A, cache = linear_activation_forward(A_prev,W,b,"relu")
caches.append(cache)
#执行1次LINEAR -> SIGMOID,并将cache缓存添加到caches列表中
W = parameters["W"+str(L)]
b = parameters["b"+str(L)]
AL,cache = linear_activation_forward(A,W,b,"sigmoid")
caches.append(cache)
assert (AL.shape == (1,X.shape[1])) # 1 代表最后一层神经单元的个数为 1 个
return AL,caches
#计算损失函数
def compute_cost(AL,Y):
"""
param :
AL -- 与标签预测相关的向量,维度为:(1,样本数目)
Y -- 标签的真实值,举例:图片中是猫值为1,不是猫值为0,维度为:(1,样本数目)
return:
cost -- 交叉熵成本
"""
m = Y.shape[1] #样本个数
cost = (1./m) * (-np.dot(Y,np.log(AL).T) - np.dot(1-Y,np.log(1-AL).T))
cost = np.squeeze(cost) #让cost的维度是我们想要的,如转换[[17]]为17
assert (cost.shape == ())
return cost
#反向传播——线性部分
def linear_backward(dZ,cache):
"""
实现单层反向传播的线性部分(l层)
param :
dZ -- 关于当前层L的线性输出Z的成本函数的梯度
cache -- 当前层前向传播的元组的值(a_prev,W,b)
return:
dA_prev -- 成本函数对前一层第l-1层的激活值的梯度,维度为:与A_prev相同
dW -- 成本函数对当前层第l层的W值的梯度,维度为:与W相同
db -- 成本函数对当前层第l层的b值的梯度,维度为:与b相同
"""
A_prev,W,b = cache
m = A_prev.shape[1] #样本数目
dW = np.dot(dZ,A_prev.T)/m
db = np.sum(dZ,axis=1,keepdims=True)/m
dA_prev = np.dot(W.T,dZ)
assert (dA_prev.shape == A_prev.shape)
assert (dW.shape == W.shape)
assert (db.shape == b.shape)
return dA_prev,dW,db
#反向传播——线性--激活部分
def linear_activation_backward(dA,cache,activation):
"""
对LINEAR->ACTIVATION层执行反向传播
param :
dA -- 对当前层(l层)激活值的梯度
cache -- 元祖值(linear_cache, activation_cache),存储起来方便后续反向传播计算
activation -- 当前层用到的激活函数,以文本字符串存储,为"sigmoid"或"relu"
return:
dA_prev -- 成本函数对前一层第l-1层的激活值的梯度,维度为:与A_prev相同
dW -- 成本函数对当前层第l层的W值的梯度,维度为:与W相同
db -- 成本函数对当前层第l层的b值的梯度,维度为:与b相同
"""
linear_cache, activation_cache = cache
if activation == "relu":
dZ = relu_backward(dA,activation_cache)
dA_prev, dW, db = linear_backward(dZ,linear_cache)
elif activation == "sigmoid":
dZ = sigmoid_backward(dA,activation_cache)
dA_prev, dW, db = linear_backward(dZ,linear_cache)
return dA_prev,dW,db
#反向传播——L层深层神经网络整体部分
def L_model_backward(AL,Y,caches):
"""
对[LINEAR->RELU] * (L-1) -> LINEAR -> SIGMOID计算反向传播
param :
AL -- 预测值构成的向量,正向传播函数L_model_forward()的输出值
Y -- 包含真实标签值的向量(0 if non-cat, 1 if cat)
cache --caches缓存列表,包括如下:
L-1个 linear_relu_forward()函数的cache缓存,下标为:0 至 L-2
1个 linear_sigmoid_forward()函数的cache缓存,下标为:L-1
return:
grads -- 关于梯度的字典
grads["dA" + str(l)] = ...
grads["dW" + str(l)] = ...
grads["db" + str(l)] = ...
"""
grads = {}
L = len(caches) #深层神经网络的层数
m = AL.shape[1] #样本数目
Y = Y.reshape(AL.shape) #Y与AL的维度相同
#反向传播初始化
dAL = -(np.divide(Y,AL) - np.divide(1 - Y,1 - AL))
#第L层(SIGMOID -> LINEAR)的梯度,
# 输入: "AL, Y, caches". 输出: "grads["dAL"], grads["dWL"], grads["dbL"]
current_cache = caches[L-1] #最后一层对应最后一个缓存
grads["dA"+str(L)],grads["dW"+str(L)],grads["db"+str(L)] = linear_activation_backward(dAL,current_cache,"sigmoid")
for l in reversed(range(L-1)):
#第l层:(RELU -> LINEAR)的梯度
#输入:grads["dA" + str(l + 2)], caches. 输出:grads["dA"+str(l+1), grads["dW"+str(l+1)] , grads["db"+str(l+1)]
current_cache = caches[l]
dA_prev_temp,dW_temp,db_temp = linear_activation_backward(grads["dA"+str(l+2)],current_cache,"relu")
grads["dA"+str(l+1)] = dA_prev_temp
grads["dW"+str(l+1)] = dW_temp
grads["db"+str(l+1)] = db_temp
return grads
#更新参数
def update_parameters(parameters,grads,learning_rate):
"""
利用梯度下降更新参数
param :
parameters -- python字典形式的参数
grads -- python字典形式保存的梯度,L_model_backward函数的输出
learning_rate -- 学习率
return:
parameters -- python字典形式的更新后的参数
parameters["W" + str(l)] = ...
parameters["b" + str(l)] = ...
"""
L = len(parameters) // 2 #深层神经网络的层数
#利用for循环执行每个参数的更新
for l in range(L):
parameters["W"+str(l+1)] = parameters["W"+str(l+1)] - learning_rate * grads["dW"+str(l+1)]
parameters["b"+str(l+1)] = parameters["b"+str(l+1)] - learning_rate * grads["db"+str(l+1)]
return parameters
def predict(X,y,parameters):
"""
预测L层神经网络的结果
param :
X -- 输入数据集
y -- 真实的标签
parameters -- 训练集中的训练的参数
return:
p -- 对于给定的数据集的预测
"""
m = X.shape[1] #样本数目
n = len(parameters) // 2 #神经网络的层数
p = np.zeros((1,m))
#前向传播
probas,caches = L_model_forward(X,parameters)
for i in range(0,probas.shape[1]):
if probas[0,i] > 0.5:
p[0,i] = 1
else:
p[0,i] = 0
print("Accuracy: "+str(np.sum((p == y)/m)))
return p
def print_mislabeled_images(classes,X,y,p):
"""
画出预测值与真实值不同的图片
param :
classes -- 所有分类标签
X -- 数据集
y -- 真实标签值
p -- 预测标签值
"""
a = p + y
mislabeled_indices = np.asarray(np.where(a == 1))
plt.rcParams['figure.figsize'] = (40.0, 40.0) # set default size of plots
num_images = len(mislabeled_indices[0])
for i in range(num_images):
index = mislabeled_indices[1][i]
plt.subplot(2, num_images, i + 1)
plt.imshow(X[:, index].reshape(64, 64, 3), interpolation='nearest')
plt.axis('off')
plt.title("Prediction: " + classes[int(p[0, index])].decode("utf-8") + " \n Class: "
+ classes[y[0, index]].decode("utf-8"))3、模型构建完成后,可以使用经过训练的参数对测试数据集进行图像分类,打印出在测试集上的准确率。
可能注意到,在较少的迭代次数(例如,1500)上在测试集上运行模型提供了更好的精确度。
这叫做“early stopping”,early stopping 是一种防止过拟合。
(五)L层深层神经网络模型构建
结构为: [LINEAR -> RELU] × (L-1) -> LINEAR -> SIGMOID
假如构建一个5层的深度神经网络,每层的神经节点数目为:[12288, 20, 7, 5, 1]
模型构建完成后,可以使用经过训练的参数对测试数据集进行图像分类,打印出在测试集上的准确率。
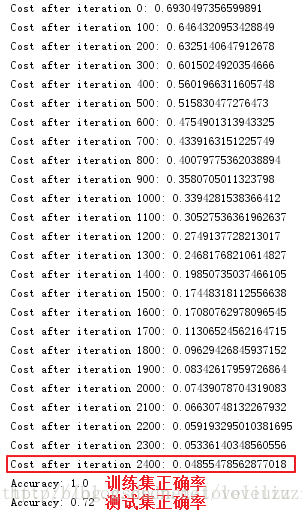
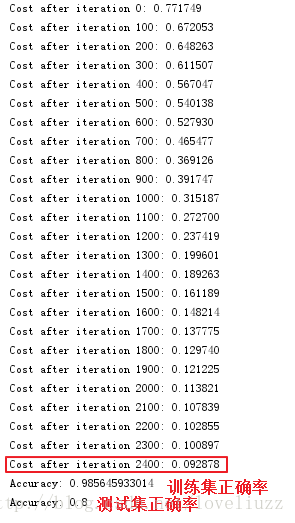
(六)总结
通过比较,5层的深层神经网络在测试集的准确率为0.8,相比于2层的神经网络在测试集的准确率为0.72,
有很好的表现性能。下面打印出在深层神经网络里面被错误标记的图片,可总结出模型表现不佳的
几种类型的图像,包括:
1、猫的身体在异常的位置。 2猫出现在类似颜色的背景下。 3、不常见的猫色和种类。4、相机角度。
5、图片的亮度。6、尺度变化(图像中的猫非常大或非常小)
(七)用自己的图片进行测试
主体的代码存放在 DNN_application.py 文件中:
#!/usr/bin/env python
# -*- coding:utf-8 -*-
# Author:ZhengzhengLiu
import time
import numpy as np
import pylab
import matplotlib.pyplot as plt
import h5py #数据集库
import scipy #高级的科学计算库,操控Numpy数组来进行科学计算
from scipy import ndimage #数学形态学的方法,如:腐蚀运算、膨胀运算、开/闭运算
from PIL import Image #python图像处理库
from lr_utils import load_dataset #加载数据集
from dnn_app_utils_v2 import *
plt.rcParams["figure.figsize"] = (5.0,4.0) #显示图像的最大范围
plt.rcParams["image.interpolation"] = "nearest" #插值方式
plt.rcParams["image.cmap"] = "gray" #灰度空间
np.random.seed(1)
#加载数据集(cat/non-cat)
train_x_orig,train_y,test_x_orig,test_y,classes = load_dataset()
#展示其中一张图片
index = 8
plt.savefig("")
plt.imshow(train_x_orig[index])
pylab.show() #解决pycharm中plt.imshow不显示图片
print("y = "+str(train_y[0,index])+".It's a "+classes[train_y[0,index]].decode("utf-8")+" picture")
#打印数据集的相关信息
m_train = train_x_orig.shape[0]
num_px = train_x_orig.shape[1]
m_test = test_x_orig.shape[0]
print("Number of training examples:"+str(m_train))
print("Number of testing examples:"+str(m_test))
print("Each image of size:("+str(num_px)+","+str(num_px)+",3)")
print("train_x_orig shape:"+str(train_x_orig.shape))
print("train_y shape:"+str(train_y.shape))
print("test_x_orig shape:"+str(test_x_orig.shape))
print("test_y shape:"+str(test_y.shape))
#训练集合测试集的图片reshape的向量化处理
train_x_flatten = train_x_orig.reshape(train_x_orig.shape[0],-1).T # -1:重构使得剩余维度拉伸
test_x_flatten = test_x_orig.reshape(test_x_orig.shape[0],-1).T
#标准化特征值,使得数值在0至1之间
train_x = train_x_flatten/255.
test_x = test_x_flatten/255.
print("train_x's shape:"+str(train_x.shape))
print("test_x's shape:"+str(test_x.shape))
# #定义模型的常量
# n_x = 12288 # num_px * num_px * 3(输入层神经单元数目)
# n_h = 7 #隐藏层神经单元数目
# n_y = 1 #输出层神经单元数目
# layers_dims = (n_x,n_h,n_y)
#
# #两层神经网络模型
# def two_layer_module(X,Y,layers_dims,learning_rate=0.0075,num_iterations=3000,print_cost=False):
# """
# 两层神经网络:LINEAR->RELU->LINEAR->SIGMOID
# param :
# X -- 输入数据,维度大小为(n_x,样本数目)
# Y -- 真实的标签构成的向量,(1 if cat,0 if non-cat),维度大小为(1,样本数目)
# layers_dims -- 每层的神经单元数目
# learning_rate -- 学习率,梯度下降更新的规则
# num_iterations -- 优化循环的迭代次数
# print_cost -- 设置为True,将会每隔100次迭代打印一下目标函数的值
#
# return:
# parameters -- 包含W1, W2, b1, 和b2 的字典形式
# """
# np.random.seed(1)
# grads = {}
# costs = [] #保存目标值
# m = X.shape[1] #样本数目
# (n_x, n_h, n_y) = layers_dims
#
# #初始化字典形式的参数
# parameters = initialize_parameters(n_x, n_h, n_y)
#
# #从字典形式的参数中得到 W1, b1, W2 和 b2
# W1 = parameters["W1"]
# b1 = parameters["b1"]
# W2 = parameters["W2"]
# b2 = parameters["b2"]
#
# #循环梯度下降
# for i in range(0,num_iterations):
# #前向传播,LINEAR -> RELU -> LINEAR -> SIGMOID.
# # 输入: "X, W1, b1". 输出: "A1, cache1, A2, cache2".
# A1,cache1 = linear_activation_forward(X,W1,b1,"relu")
# A2,cache2 = linear_activation_forward(A1,W2,b2,"sigmoid")
#
# #计算损失/目标函数
# cost = compute_cost(A2,Y)
#
# #初始化反向传播参数
# dA2 = -(np.divide(Y,A2) - np.divide(1-Y,1-A2))
#
# #反向传播,输入:dA2, cache2, cache1,输出:dA1, dW2, db2; dA0 (not used), dW1, db1
# dA1, dW2, db2 = linear_activation_backward(dA2,cache2,"sigmoid")
# dA0,dW1,db1 = linear_activation_backward(dA1,cache1,"relu")
#
# grads["dW1"] = dW1
# grads["db1"] = db1
# grads["dW2"] = dW2
# grads["db2"] = db2
#
# #更新参数
# parameters = update_parameters(parameters,grads,learning_rate)
#
# W1 = parameters["W1"]
# b1 = parameters["b1"]
# W2 = parameters["W2"]
# b2 = parameters["b2"]
#
# #每100次循环迭代打印一次目标函数值
# if print_cost and i%100 == 0:
# print("Cost after iteration {}: {}".format(i,np.squeeze(cost)))
# if print_cost and i%100 == 0:
# costs.append(cost)
#
# #画出目标函数值曲线 plt cost
# plt.plot(np.squeeze(costs))
# plt.ylabel("cost")
# plt.xlabel("iteration (per tens)")
# plt.title("learning rate = "+str(learning_rate))
# plt.savefig("2 layters NN.png")
# plt.show()
#
# return parameters
#
# parameters = two_layer_module(train_x,train_y,layers_dims=(n_x,n_h,n_y),num_iterations=2500,print_cost=True)
#
# #预测
# predictions_train = predict(train_x,train_y,parameters)
#
# predictions_test = predict(test_x,test_y,parameters)
#L层深层神经网络模型——5层
layers_dims = [12288,20,7,5,1]
def L_layer_model(X,Y,layers_dims,num_iterations=1000,learning_rate=0.0075,print_cost=False):
np.random.seed(1)
costs = []
parameters = initialize_parameters_deep(layers_dims)
for i in range(num_iterations):
#前向传播
AL,caches = L_model_forward(X,parameters)
#计算目标函数
cost = compute_cost(AL,Y)
#反向传播
grads = L_model_backward(AL,Y,caches)
#参数更新
parameters = update_parameters(parameters,grads,learning_rate)
# 每100次循环迭代打印一次目标函数值
if print_cost and i%100 == 0:
print("Cost after iteration %i: %f"%(i,cost))
if print_cost and i%100 == 0:
costs.append(cost)
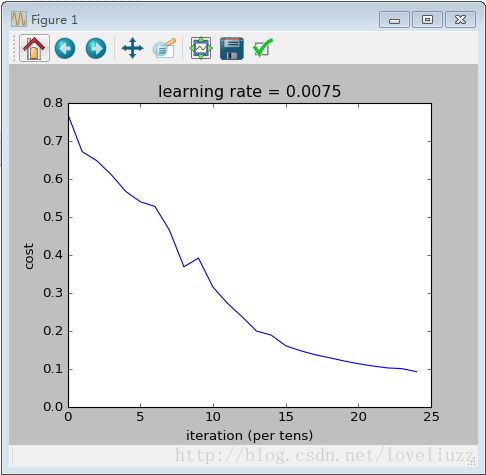
#画出目标函数值曲线 plt cost
plt.plot(np.squeeze(costs))
plt.ylabel("cost")
plt.xlabel("iteration (per tens)")
plt.title("learning rate = "+str(learning_rate))
plt.savefig("L layters NN.png")
plt.show()
return parameters
parameters = L_layer_model(train_x,train_y,layers_dims,num_iterations=2500,print_cost=True)
#预测
predictions_train = predict(train_x,train_y,parameters)
predictions_test = predict(test_x,test_y,parameters)
#打印出在深层神经网络里面被错误标记的图片
print_mislabeled_images(classes,test_x,test_y,predictions_test)
#用自己的图片进行测试
my_image = "my_image.jpg" # 可以改成你自己的图片为文件名
my_label_y = [1] #图片的真实分类值(1 -> cat, 0 -> non-cat)
fname = "images/" + my_image
image = np.array(ndimage.imread(fname, flatten=False))
my_image = scipy.misc.imresize(image, size=(num_px,num_px)).reshape((num_px*num_px*3,1))
my_predicted_image = predict(my_image, my_label_y, parameters)
plt.imshow(image)
pylab.show() #解决pycharm中plt.imshow不显示图片
print ("y = " + str(np.squeeze(my_predicted_image)) + ", your L-layer model predicts a \"" + classes[int(np.squeeze(my_predicted_image)),].decode("utf-8") + "\" picture.")