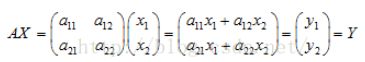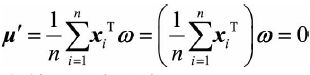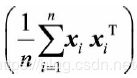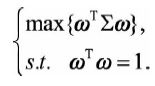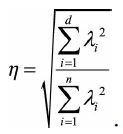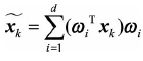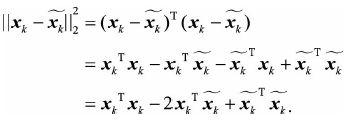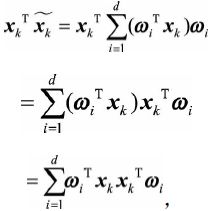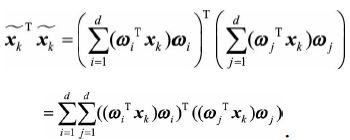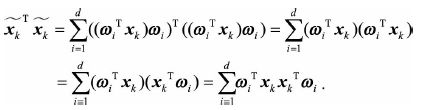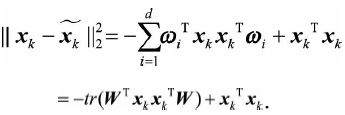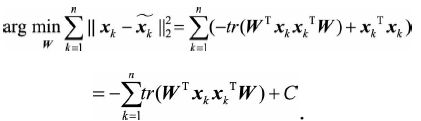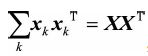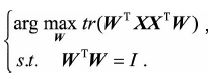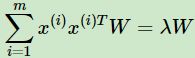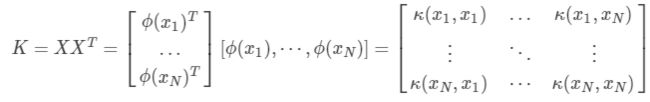个人总结：降维 PCA的两种解释与推导
降维
在维度灾难、冗余，这些在数据处理中常见的场景，不得不需要我们进一步处理，为了得到更精简更有价值的信息，我们所用的的各种方法的统称就是降维。
降维有两种方式：
（1）特征抽取：我觉得叫做特征映射更合适。因为它的思想即把高维空间的数据映射到低维空间。比如马上要提到的PCA即为一种特征映射的方法。还有基于神经网络的降维等。
（2）特征选择：
- 过滤式（打分机制）：过滤，指的是通过某个阈值进行过滤。比如经常会看到但可能并不会去用的，根据方差、信息增益、互信息、相关系数、卡方检验来选择特征。
- 包裹式：每次迭代产生一个特征子集，评分。
- 嵌入式：先通过机器学习模型训练来对每个特征得到一个权值。接下来和过滤式相似，通过设定某个阈值来筛选特征。区别在于，嵌入式使用机器学习训练；过滤式采用统计特征。
PCA Principal components analysis主成分分析，在压缩消除冗余和数据噪音消除等有广泛应用。
首先复习一下特征值和特征向量
这里复习一下特征值和特征向量，理解内在的含义。
A是n阶矩阵，λ和n维非零向量x使关系式：
Ax = λx .....(1) λ为矩阵A的特征值，x为对应特征值λ的特征向量。 也可以写成（A - λE）x = 0 .....(2)
如何理解上面两个式子？
首先要理解矩阵线性变换，即矩阵乘法：
向量X通过矩阵A这个变化规则就可以变换为向量Y了。
几何变换如下图所示：
X由(x1, x2)这个向量构成，Y由(a11x1 + a12x2, a21x1 + a22x2)构成。
由 Ax = λx .....(1) 可知：
确定了特征值后，向量x变换为：
引用《线性代数的几何意义》的描述：“矩阵乘法对应了一个变换，是把任意一个向量变成另一个方向或长度都大多不同的新向量。在这个变换的过程中，原向量主要发生旋转、伸缩的变化。如果矩阵对某一个向量或某些向量只发生伸缩变换，不对这些向量产生旋转的效果，那么这些向量就称为这个矩阵的特征向量，伸缩的比例就是特征值。”
显然，第一个图就是发生了旋转、伸缩，第二个图仅仅发生了伸缩。
特征值对应的特征向量就是理想中想取得的正确坐标轴，而特征值就等于数据在旋转后的坐标上对应维度的方差。
通过求出A的特征值和对应的特征向量，就能找到旋转后正确的坐标轴，这个就是特征值和特征向量的一个实际应用：“得出使数据在各个维度区分达到最大的坐标轴”。（区分大：方差大）
而在数据挖掘中，就会直接用特征值来描述对应特征向量方向上包含的信息量，而某一特征值除以所有特征值的和的值就为：该特征向量的方差贡献率。（在该维度下蕴含的信息的比例）
经过特征向量变换下的数据称为变量的主成分，当前m各主成分累计的方差贡献率达到85%以上就保留这个m个主成分的数据。实现了对数据进行降维的目的。
PCA的目的
PCA的目的：最小投影距离，最大投影方差。降维后不同维度的相关性为0；
先说最大投影方差：
将图1投影到x1，显然数据离散性最大，代表数据在所投影的维度有越高的区分度，这个区分度就是信息量。
而图2投影到x1显然信息量最小（应该投影到x2）。图3投影到x1显然未完全利用其信息量。
所以当我们想对数据进行降维的话，图1就应该保留x1这个维度，图2就应该保留x2这个维度。
图3呢？图3应该考虑新的坐标轴。
将坐标轴进行旋转就能正确降维了。而这个旋转的操作其实就是矩阵变换
也就是，通过矩阵A对坐标系X进行旋转。
经过一些数学推导，其实就可以得知，特征值对应的特征向量就是理想中想取得的正确坐标轴，而特征值就等于数据在旋转后的坐标上对应维度的方差（沿对应的特征向量的数据的方差）。
而A其实即为我们想求得的那个降维特征空间，Y则是我们想要的降维后的数据。
PCA的过程：我们为什么这么做（通过最大投影方差进行推导）
（1）采用了中心化，均值为0。未中心化，可能第一主成分的方向有误
这里可以看出主成分分析的目的是最小投影距离，最大投影方差。如果不中心化就达不到上述目的。
在中心化后，由于特征的均值变为0，所以数据的协方差矩阵C可以用E(XXT)或者1/m * XXT来表示，XT为矩阵的转置。这里X每一行为一个特征。当然也可以表示为E(XTX)或者1/m * XTX，这时每一行为一个样本。
（2）标准化数据，为什么要标准化，因为等下要算特征值和特征向量，特征值对应的特征向量就是理想中想取得的正确坐标轴，而特征值就等于数据在变换后的坐标上对应维度的方差（沿对应的特征向量的数据的方差）。
我们可以验证一下：
这里X作为原始空间的数据，有五条，每条数据有两个特征。
X_cov是X的协方差矩阵（这里算协方差，numpy采用除以m-1，是样本方差，在实际生活中比除以m的总体方差应用更多，但在这里不管除以多少都无伤大雅）。
X_con eig是协方差矩阵的特征值，里面还有特征向量（标准正交基），至于为什么强调标准正交基，后续会解释。
change zone是将原始空间的数据经过特征空间变换（将原始数据乘以特征空间）后得到的数据。
X change cov是变换后的数据的协方差矩阵，我们已经可以发现变换后数据的方差（对角线上的值）与特征值相等。
如果我们不将特征向量标准化呢？
这里使用了测试的特征向量（1,-1）和（1,1）。可以发现最后变换域的方差和之前的特征值是一个倍数关系！但是这仍然可以证明，选用更大特征值的特征向量进行降维，可以使变换后的数据保持方差更大。
而考虑这样一个例子，一个特征表示对象的长度（米为单位），而第二个特征表示对象的宽度（厘米为单位）。如果数据没有被标准化，那么最大方差及最大特征向量将隐式地由第一个特征定义。
这里可以发现，经过中心化和标准化的数据，均值为0，方差为1（但还是服从原始分布）。假设此时的数据为X，X有m个n维数据，(x(1),x(2),...,x(m))。
（3）算协方差矩阵。这里把n维特征两两求协方差，刚刚已经说过，去中心化后，此时的协方差矩阵为E(XXT)【参见协方差矩阵公式】或者1/m * XXT。为什么要算协方差矩阵呢？这时就要想起我们之前的目的：在降维后的每一维度上，方差最大。而方差最大，则容易想到的就是协方差矩阵，去中心化后，协方差矩阵的对角线上的值正好就是各个数据维度的方差。原始数据的协方差矩阵X[nxn]对角线，对应的就是原始数据的方差；降维后的数据的协方差矩阵X' [n'xn']，对应的就是降维后的数据的方差。而我们的目的，则是使方差最大，这就又想到了另一个概念，迹，因为迹不就是对角线上所有元素之和吗，而协方差矩阵的迹，不就是方差之和吗。这样我们构建损失函数，不就是argmax(协方差矩阵X’的迹) 吗。
推导一下：
首先设新的坐标系为W [n' x n']， 为
，显然w为标准正交基。
在新的坐标系的投影为Z = WTX，其中Z为 {z1, z2, ... z_n'}。
向量
在ω上的投影坐标可以表示为
易知中心化后，投影之后的均值为0，即
投影之后的方差可以表示为
其实就是样本协方差矩阵，所以问题可以转化为、
结合目标函数与条件，用
代替协方差矩阵，通过拉格朗日函数可以得到：
对ω进行求导：
此时求出来方差D(x)为
−λ是由特征值构成的对角阵，且特征值在对角线上，其余位置为0。很显然，W为标准正交基，我们假如把特征值以及对应的W的那一列拿出来和
（4）刚刚说了需求是前n’个最大的特征值以及对应的特征向量。于是就很容易想到对协方差矩阵进行SVD分解，或者也可以说特征值分解，选取最大的几个特征值（或者设置阈值来选最大的几个特征值），对应的特征向量进行标准化（使其成为标准正交基）后组成特征矩阵，这些特征向量都是正交的。
复习一下SVD分解（奇异值分解）：来自维基百科
MMT就是一个 m x m阶的矩阵，这个矩阵的所有特征向量组成的矩阵就是U。这里面每个特征向量就是左奇异向量。
所以MTM就是一个 n x n阶的矩阵，这个矩阵的所有特征向量组成的矩阵就是V。这里面每个特征向量就是右奇异向量。
而我们要找的，也就是MTM的特征向量。
所以通过SVD分解就能求出我们需要的对应的特征值，以及需要的特征空间，而实际上在sklearn中PCA背后的算法就是用的SVD，而不是暴力特征分解。
定义降维后的空间信息占比为
PCA的过程：我们为什么这么做（通过最小投影距离进行推导）
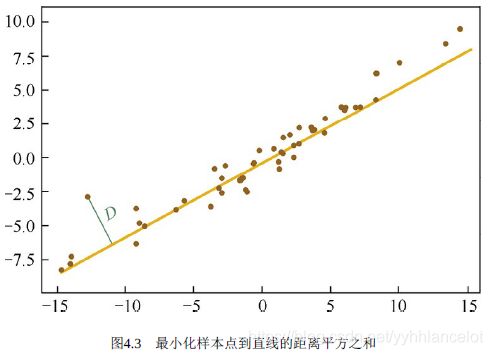
通过最小投影距离其实是和线性回归的原理类似。
我们希望投影后到d维超平面，最小化所有点到投影点的距离平方之和。
为原始点经过变换到新的特征空间的点。数据集每个点到投影点的距离为
表示在超平面D上的投影点（投影向量），该超平面由d个标准正交基
构成，于是投影向量可以表示为
表示在ωi方向上投影的长度。PCA要优化的方法目标为
其中损失函数可以展开
第一项的
是一个常数，将之前表示的代入上式第二三项，注意
和
表示投影长度，都是常数
由于当i不等于j时，
，因此只剩下1
实际是矩阵
的迹，将其代入得到
因此损失函数可以写为
又由于矩阵乘法性质
，所以问题可以转化为
这其实就已经和上面用最大方差理论等价了，再使用同样的步骤就可以求得最终的投影空间，最佳投影方向就是最大特征值所对应的特征向量。
核主成分分析KernelizedPCA介绍
有时我们的数据并不是可以投影到线性超平面的，这时候就不能直接进行PCA降维，这里就需要用到支持向量机一样的核函数的思想，先把数据从n维映射到线性可分的高维N>n，然后再从N维降维到一个低维度n'，这里的维度之间满足n' < n < N。
通过映射φ将n维映射到N维。
对于n维空间的特征分解：
映射为：
通常φ不是显式的，计算的时候通过核函数完成。
其中核函数有
更多的细节就不进行深入阐述了，感兴趣的读者可以自行百度。
PCA总结
为了克服PCA的一些缺点，也衍生出了很多PCA的变种，包括上述提到的KPCA。
PCA的主要优点有：
（1）仅通过方差衡量信息量，不受数据集以外因素影响。
（2）各主成分之间正交，消除可能出现的低秩、或者原始数据成分间相关的可能。
（3）计算方法简单，易于实现。
主要缺点：
（1）降维后各个特征维度的含义具有一定的模糊性，数据的可解释性没有原始样本的特征强。（可解释性变弱）
（2）方差小的非主成分可能含有对样本差异的重要信息（可能丢失强力特征），因降维丢弃后可能对后续处理有影响。