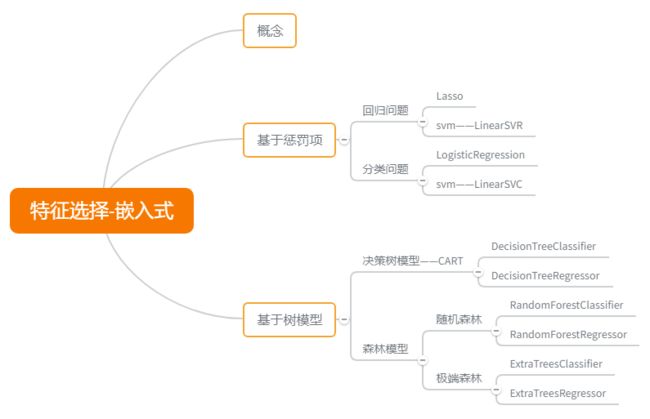
特征选择-嵌入式选择

嵌入式特征选择是将特征选择过程与学习器训练过程融为一体，两者在同一个优化过程中完成，即在学习器训练过程中自动地进行了特征选择。

基于惩罚项的特征选择法

给定数据集 $D=\{(x_1,y_1),(x_2,y_2),\cdots ,(x_n,y_n)\}$，其中 $x\in R^d,y\in R$。我们考虑最简单的线性回归模型，以平方误差为损失函数，则优化目标为
$$mi{n}_w\sum _{i=1}^n(y_i-w^T{x}_i{)}^2$$
当样本特征很多，而样本数相对较少时，上式很容易陷入过拟合。为了缓解过拟合问题，可对上式引入正则化项。

• 使用 L2 范数正则化，则称为“岭回归”（ridge regression）。

$$mi{n}_w\sum _{i=1}^n(y_i-w^T{x}_i{)}^2+\lambda ||w|{|}_2^2$$
通过引入 L2 范数正则化，确能显著降低过拟合的风险。

• 使用 L1 范数正则化，则称为 LASSO（Least Absolute Shrinkage and Selection Operator）。

$$mi{n}_w\sum _{i=1}^n(y_i-w^T{x}_i{)}^2+\lambda ||w|{|}_1$$
L1 范数和 L2 范数正则化都有助于降低过拟合风险，但 L1 范数比 L2 范数更易于获得“稀疏”（sparse）解，即它求得的 w 会有更少的非零向量。

同时使用 L1 范数和 L2 范数，即可避免过拟合，同时也实现了降维，并筛选出相应的特征。
$$mi{n}_w\sum _{i=1}^n(y_i-w^T{x}_i{)}^2+{\lambda }_1||w|{|}_1+{\lambda }_2||w|{|}_2^2$$

那么如何通过惩罚项来进行特征选择呢？对于回归问题，我们可以直接引入 Lasso，通过 Lasso 对数据集进行训练，挑选非零向量所对应的特征。

【代码实现】：Lasso 实现特征选择。

from sklearn.linear_model import Lasso
from sklearn.datasets import load_boston


# 引入数据集
dataset_boston = load_boston()
data_boston = dataset_boston.data
target_boston = dataset_boston.target

# 模型训练
model_lasso = Lasso()
model_lasso.fit(data_boston, target_boston)

# 获取权重向量
print(model_lasso.coef_)
# 输出
array([-0.06343729,  0.04916467, -0.        ,  0.        , -0.        ,
        0.9498107 ,  0.02090951, -0.66879   ,  0.26420643, -0.01521159,
       -0.72296636,  0.00824703, -0.76111454])

然后使用 sklearn.feature_selection.SelectFromModel 方法来从模型中挑选特征子集。

from sklearn.feature_selection import SelectFromModel
model_sfm = SelectFromModel(model_lasso, prefit=True)
print(model_sfm.transform(data_boston).shape)
# 输出
(506, 10)
print(data_boston.shape)
# 输出
(506, 13)

可以看出，SelectFromModel 方法剔除了权值向量为零的特征。

那么对于分类问题该如何使用惩罚项来进行特征选择呢？

【代码实现】：

from sklearn.linear_model import LogisticRegression


# 引入数据集
dataset_iris = load_iris()
data_iris = dataset_iris.data
target_iris = dataset_iris.target

# 训练模型
model_lr = LogisticRegression(penalty='l1', C=0.01)
model_lr.fit(data_iris, target_iris)
print(model_lr.coef_)
# 输出
array([[ 0.        ,  0.        , -0.18016819,  0.        ],
       [-0.03183986,  0.        ,  0.        ,  0.        ],
       [-0.00677759,  0.        ,  0.        ,  0.        ]])

# 对比添加 l1 惩罚项和没有添加 l1 惩罚项的模型
model_lr2 = LogisticRegression()
model_lr2.fit(data_iris, target_iris)
print(model_lr2.coef_)
# 输出
array([[ 0.41021713,  1.46416217, -2.26003266, -1.02103509],
       [ 0.4275087 , -1.61211605,  0.5758173 , -1.40617325],
       [-1.70751526, -1.53427768,  2.47096755,  2.55537041]])

model_sfm = SelectFromModel(model_lr, prefit=True)
print(model_sfm.transform(data_iris).shape)
# 输出
(150, 2)
print(data_iris.shape)
# 输出
(150, 4)

通过上述代码可以看到添加了 l1 惩罚项的逻辑回归模型能够对特征集做特征选择，并且在 SelectFromModel 方法的协助下挑选权值向量非零的特征。当然，我们也可以同时使用 l1 惩罚项和 l2 惩罚项，阅读本篇博客的各位可以自行实现。

除此之外，也可以使用 SVM 中的 LinearSVC 来实现分类问题的特征选择。

【代码实现】：

from sklearn.svm import LinearSVC


# 注意：dual 设置为 False，否则会报错
model_lsvc = LinearSVC(penalty='l1', C=0.01, dual=False)
model_lsvc.fit(data_iris, target_iris)
print(model_lsvc.coef_)
array([[ 0.        ,  0.21702532, -0.28757517,  0.        ],
       [ 0.        , -0.09200224,  0.        ,  0.        ],
       [-0.02505729, -0.18225482,  0.12929954,  0.        ]])
       
model_sfm = SelectFromModel(model_lsvc, prefit=True)
model_sfm.transform(data_iris).shape
# 输出
(150, 3)

SVM 包中的 LinearSVR 则可以实现对回归问题的特征选择。

【重要】：对于 SVM 和逻辑回归，参数 C 控制稀疏程度，C 越小，被选中的特征也越少；对于 Lasso，参数 alpha 越大，被选中的特征越少。

基于树模型的特征选择法

决策树可用于特征选择，树节点的划分特征所组成的集合就是选择出的特征子集。先演示决策树模型计算特征的重要度，然后再演示森林模型计算特征的重要度。

由于树模型即可用于分类问题，又可用于回归问题，因此数据集我们选择波士顿房价数据集以及鸢尾花数据集，先演示回归问题，后演示分类问题。

from sklearn.datasets import load_boston
from sklearn.datasets import load_iris

树模型-回归问题

树模型算法选用 CART，这样既可以处理连续型数据，也可以处理离散型数据，同时以基尼系数作为特征选择标准。

【实现代码】：

from sklearn.tree import DecisionTreeRegressor


dataset_boston = load_boston()
data_boston = dataset_boston.data
target_boston = dataset_boston.target
model_dtc = DecisionTreeRegressor()
model_dtc.fit(data_boston, target_boston)

# 为了方便查看，我们将精度设置为 3
np.set_printoptions(precision=3)
print(model_dtc.feature_importances_)
# 输出：
array([5.070e-02, 1.071e-03, 4.064e-03, 1.090e-03, 5.009e-02, 5.758e-01,
       1.433e-02, 7.363e-02, 3.362e-04, 1.257e-02, 7.155e-03, 1.413e-02,
       1.950e-01])

我们可以使用 sklearn.feature_selection.SelectFromModel 方法来从模型中挑选特征子集。

from sklearn.feature_selection import SelectFromModel


model_sfm = SelectFromModel(model_dtc, prefit=True)
print(model_sfm.transform(data_boston))
# 输出
array([[6.575, 4.98 ],
       [6.421, 9.14 ],
       [7.185, 4.03 ],
       ...,
       [6.976, 5.64 ],
       [6.794, 6.48 ],
       [6.03 , 7.88 ]])

SelectFromModel 能够用于拟合后拥有 coef_ 或 feature_importance 属性的模型。如果特征对应的 coef_ 或 feature_importances_ 值低于设定的阈值 threshold，那么这些特征将被移除。关于 SelectFromModel 的更多介绍和用法请参考官方文档 传送门

森林模型-回归问题

常见的森林模型有随机森林模型以及极端森林模型，在此分别演示这两种模型对回归问题特征选择的作用。

【代码实现】：随机森林

from sklearn.ensemble import RandomForestRegressor


model_rfr = RandomForestRegressor(n_estimators=50)
model_rfr.fit(data_boston, target_boston)
print(model_rfr.feature_importances_)
# 输出
array([0.036, 0.001, 0.005, 0.001, 0.024, 0.396, 0.017, 0.063, 0.003,
       0.016, 0.016, 0.013, 0.409])

model_sfm = SelectFromModel(model_rfr, prefit=True)
print(model_sfm.transform(data_boston))
# 输出
array([[6.575, 4.98 ],
       [6.421, 9.14 ],
       [7.185, 4.03 ],
       ...,
       [6.976, 5.64 ],
       [6.794, 6.48 ],
       [6.03 , 7.88 ]])

【代码实现】：极端森林

from sklearn.ensemble import ExtraTreesRegressor


model_etr = ExtraTreesRegressor(n_estimators=50)
model_etr.fit(data_boston, target_boston)
print(model_etr.feature_importances_)
# 输出
array([0.034, 0.004, 0.052, 0.016, 0.039, 0.326, 0.02 , 0.029, 0.017,
       0.044, 0.056, 0.02 , 0.342])
       
model_sfm = SelectFromModel(model_etr, prefit=True)
print(model_sfm.transform(data_boston))
# 输出
array([[6.575, 4.98 ],
       [6.421, 9.14 ],
       [7.185, 4.03 ],
       ...,
       [6.976, 5.64 ],
       [6.794, 6.48 ],
       [6.03 , 7.88 ]])

树模型-分类问题

树模型的分类问题，处理方式与树模型的回归问题相同，区别就在于调用不同的树模型方法（从 DecisionTreeRegressor 转换为 DecisionTreeClassifier），其他操作都相同。

【代码实现】：

from sklearn.tree import DecisionTreeClassifier


dataset_iris = load_iris()
data_iris = dataset_iris.data
target_iris = dataset_iris.target

model_dtc = DecisionTreeClassifier()
model_dtc.fit(data_iris, target_iris)
print(model_dtc.feature_importances_)
# 输出
array([0.027, 0.   , 0.051, 0.923])

森林模型-分类问题

【代码实现】：

model_etc = ExtraTreesClassifier(n_estimators=50)
model_etc.fit(data_iris, target_iris)
print(model_etc.feature_importances_
# 输出
array([0.06393643, 0.04529532, 0.39042913, 0.50033912])

model_rfc = RandomForestClassifier(n_estimators=50)
model_rfc.fit(data_iris, target_iris)
print(model_rfc.feature_importances_)
# 输出
array([0.07155676, 0.01874959, 0.47878474, 0.43090891])

虽然不同模型输出的特征重要程度值不同，但特征的排序（按重要程度降序排列）是一致的。

参考

• 《机器学习》周志华
• 《百面机器学习》
• 特征选择：https://blog.csdn.net/shingle_/article/details/51725054
• 特征选择 (feature_selection)：https://www.cnblogs.com/stevenlk/p/6543628.html#移除低方差的特征-removing-features-with-low-variance
• SelectKBest：https://blog.csdn.net/weixin_33962923/article/details/87837426