模拟退火算法+局部搜索算法求解TSP问题(C++实现)
实验报告――模拟退火算法求解TSP问题
项目源码:传送门
摘要:
利用模拟退火算法解决TSP问题,TSP问题的规模大小为131个城市。实验中采用多种邻域操作的局部搜索local search策略尝试解决相同规模的TSP问题,并与相同局部搜索的模拟退火算法进行对比。算法结果能找出距离TSP最优解5%到10%误差的解,这比局部搜索得出的最优解要好。通过该实验得出结论,局部搜索容易陷入局部最优解,而模拟退火利用其一定概率接受差解的特性跳出局部最优,从而能逐渐收敛到全局最优。
1.导言
要解决的问题:TSP问题,假设一个旅行商人要去n个城市,他必须经过且只经过每个城市一次,要求最后回到出发的城市,并且要求他选择的路径是所有路径中的最小值 。TSP问题是一个组合优化问题,该问题如果用穷举的方法解决,解的空间范围是指数级的。迄今为止,这类问题中没有一个找到有效算法,是NP难问题。
拟使用的方法:模拟退火算法(Simulated Annealing Algorithm)是元启发式搜索算法的其中一种。相比起效率低下的随即搜索算法,元启发式搜索算法借助了演化思想和集群智能思想,对解的分布有规律的复杂问题有良好的效果。
模拟退火法(Simulated Annealing)是克服爬山法缺点的有效方法,所谓退火是冶金专家为了达到某些特种晶体结构重复将金属加热或冷却的过程,该过程的控制参数为温度T。模拟退火法的基本思想是,在系统朝着能量减小的趋势这样一个变化过程中,偶尔允许系统跳到能量较高的状态,以避开局部极小点,最终稳定到全局最小点。
算法的关键问题是:
- 初温与接受温度的设置
- 局部搜索的方法
- 退火系数
- 某一温度下的内循环次数
2.实验过程
算法流程
- 随机挑选出一单元,并给他一个随机的位移 k k k,求出系统因此而产生的能量变化 Δ E k \Delta E_k ΔEk。
- 若 Δ E k ≤ 0 \Delta E_k \leq0 ΔEk≤0,该位移可采纳,而变化后的系统状态可作为下次变化的起点;若 Δ E k > 0 \Delta E_k \gt0 ΔEk>0,位移后的状态可采纳的概率为
P k = 1 ( 1 + e − Δ E k / T ) P_k = \frac{1}{(1+e^{-\Delta E_k/T})} Pk=(1+e−ΔEk/T)1
式中T为温度,然后从(0,1)区间均匀分布的随机数中挑选一个数R。若 R < P k R \lt P_k R<Pk,则将变化后的状态作为下次的起点;否则,将变化前的状态作为下次的起点。
3. 转第(1)步继续执行,直至达到平衡状态为止。
1.进行局部搜索找最优解
a. 统计一个解的长度
评价函数是寻找最优解的一个关键,TSP问题可以利用解的路径长度作为评价该解的优秀程度。
统计长度也很简单,从头到尾遍历城市数组,将邻近的两个城市拿出来根据坐标来进行计算直线距离,最后累加起来即可。
double distance(double *city1, double *city2) {
double x1 = *city1;
double y1 = *(city1 + 1);
double x2 = *(city2);
double y2 = *(city2 + 1);
double dis = sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2));
return dis;
}
double path_len(int *arr) {
double path = 0;
int index = *arr; // 城市序号
for (int i = 0; i < N - 1; i++) {
int index1 = *(arr + i); // 起点
int index2 = *(arr + 1 + i); // 终点
double dis = distance(city_pos[index1 - 1], city_pos[index2 - 1]);
path += dis;
}
// 计算回路
int last_index = *(arr + N - 1); // 最后一个城市序号
int first_index = *arr; // 第一个城市序号
double last_dis = distance(city_pos[last_index - 1], city_pos[first_index - 1]);
path += last_dis;
return path;
}
b.四种局部搜索的策略
这里,我们设置了四种局部搜索的策略来进行找邻域中的解。
(1) 交换两位置
随机找到两个位置,要求这两个位置不相同,交换这两个位置的值
// 交换两位置
if (p <= 0.25) {
double r1 = ((double)rand()) / (RAND_MAX + 1.0);
double r2 = ((double)rand()) / (RAND_MAX + 1.0);
int pos1 = (int)(N * r1); // 第一个交叉点位置
int pos2 = (int)(N * r2); // 第二个交叉点位置
while (pos1 == pos2) {
r1 = ((double)rand()) / (RAND_MAX + 1.0);
r2 = ((double)rand()) / (RAND_MAX + 1.0);
pos1 = (int)(N * r1); // 第一个交叉点位置
pos2 = (int)(N * r2); // 第二个交叉点位置
}
int temp = city_list[pos1];
city_list[pos1] = city_list[pos2];
city_list[pos2] = temp;
}
(2) 翻转一段序列
随机找到两个点,将这两个点的序列进行翻转
// 序列翻转
else if (p > 0.25 && p <= 0.50) {
double r1 = ((double)rand()) / (RAND_MAX + 1.0);
double r2 = ((double)rand()) / (RAND_MAX + 1.0);
int pos1 = (int)(N * r1); // 第一个交叉点位置
int pos2 = (int)(N * r2); // 第二个交叉点位置
while (pos1 == pos2) {
r1 = ((double)rand()) / (RAND_MAX + 1.0);
r2 = ((double)rand()) / (RAND_MAX + 1.0);
pos1 = (int)(N * r1); // 第一个交叉点位置
pos2 = (int)(N * r2); // 第二个交叉点位置
}
int p1 = min(pos1, pos2);
int p2 = max(pos1, pos2);
for (int i = p1,j = p2; i < j; i++,j--) {
int temp = city_list[p1];
city_list[p1] = city_list[p2];
city_list[p2] = temp;
}
}
(3) 调转左右两边序列
随机找到两个点,将这两个点的左右两个序列进行调转
double r1 = ((double)rand()) / (RAND_MAX + 1.0);
double r2 = ((double)rand()) / (RAND_MAX + 1.0);
int pos1 = (int)(N * r1); // 第一个交叉点位置
int pos2 = (int)(N * r2); // 第二个交叉点位置
while (pos1 == pos2) {
r1 = ((double)rand()) / (RAND_MAX + 1.0);
r2 = ((double)rand()) / (RAND_MAX + 1.0);
pos1 = (int)(N * r1); // 第一个交叉点位置
pos2 = (int)(N * r2); // 第二个交叉点位置
}
int* path_temp = new int[N];
memcpy(path_temp, city_list, N * sizeof(int));
int p1 = min(pos1, pos2);
int p2 = max(pos1, pos2);
int pos = 0;
for (int i = p2; i < N; i++) {
city_list[pos++] = path_temp[i];
}
for (int i = p1+1; i < p2; i++) {
city_list[pos++] = path_temp[i];
}
for (int i = 0; i <= p1; i++) {
city_list[pos++] = path_temp[i];
}
free(path_temp);
(4) 提取一段序列放到路径的头部
随机找到两个点,要求两个点不能相同,提取该序列放到路径的头部
else if (p > 0.50 && p <= 0.75) {
double r1 = ((double)rand()) / (RAND_MAX + 1.0);
double r2 = ((double)rand()) / (RAND_MAX + 1.0);
int pos1 = (int)(N * r1); // 第一个交叉点位置
int pos2 = (int)(N * r2); // 第二个交叉点位置
while (pos1 == pos2) {
r1 = ((double)rand()) / (RAND_MAX + 1.0);
r2 = ((double)rand()) / (RAND_MAX + 1.0);
pos1 = (int)(N * r1); // 第一个交叉点位置
pos2 = (int)(N * r2); // 第二个交叉点位置
}
int* path_temp = new int[N];
memcpy(path_temp, city_list, N * sizeof(int));
city_list[0] = path_temp[pos1];
city_list[1] = path_temp[pos2];
int pos = 2;
for (int i = 0; i < N; i++) {
if (i == pos1 || i == pos2) continue;
city_list[pos++] = path_temp[i];
}
free(path_temp);
}
c. 设置循环次数,局部搜索
局部搜索仅接受好解,当遇到差解时,保留旧解。循环多次直到解不再改变,这时说明局部搜索进入了局部最优解,而且无法跳出来。
while (count <= LOOP_TIME) {
memcpy(city_list_copy, city_list, N * sizeof(int)); // 复制数组
create_new(); // 产生新解
f1 = path_len(city_list_copy);
f2 = path_len(city_list);
df = f2 - f1;
// 好解全部接受
if(df < 0){
outfile2 << path_len(city_list) << endl;
cout <<"当前最优解: " << path_len(city_list) << endl;
count_output++;
}
// 否则保存旧值
else{
if(count%1000 == 0){
cout << "最优解无变化,仍为"<< path_len(city_list_copy) << endl;
}
memcpy(city_list, city_list_copy, N * sizeof(int));
}
}
2.添加模拟退火算法
在局部搜索的基础上,不改变局部搜索的策略,仅仅添加上温度的控制,以此来让算法在一定的概率下接受差解。
参数设定
定义初始温度为50000,接受温度为0.00001,退火系数为0.99(即 T i + 1 = 0.99 ∗ T i T_{i+1} = 0.99 * T_i Ti+1=0.99∗Ti)
每个温度内循环为10000次
#define T0 50000.0 // 初始温度
#define T_end 0.00001 // 接受温度
#define q 0.99 // 退火系数
#define L 10000 // 每个温度时的迭代次数
#define N 131 // 城市数量
将局部搜索加入到每一个温度下的循环中,并且找到一个新解时候,判断其与旧解的差值。利用这个插值以及温度来设定概率,用这个概率判断是否接受这个差解,当然好解仍然是全部接受。
执行完一次温度的10000次内循环,进行降温操作。
while (T > T_end) {
for (int i = 0; i < L; i++) {
memcpy(city_list_copy, city_list, N * sizeof(int)); // 复制数组
create_new(); // 产生新解
f1 = path_len(city_list_copy);
f2 = path_len(city_list);
df = f2 - f1;
// 退火准则
if (df >= 0) {
r = ((double)rand()) / (RAND_MAX);
// 保留原来的解
if (exp(-df / T) <= r) {
memcpy(city_list, city_list_copy, N * sizeof(int));
}
}
}
T *= q; // 降温
count++;
}
3.结果分析
实验环境: Windows10
a.局部搜索算法的结果
结果图表展示:
| 次数 | 最优解 | 误差 | 运行时间 |
|---|---|---|---|
| 1 | 736.45 | 30.57% | 27.32s |
| 2 | 686.35 | 21.69% | 30.16s |
| 3 | 726.87 | 28.88% | 30.32s |
| 4 | 672.25 | 19.19% | 27.89s |
| 5 | 723.39 | 28.26% | 30.53s |
| 6 | 699.15 | 23.96% | 28.17s |
| 7 | 697.47 | 23.66% | 27.84s |
| 8 | 663.63 | 17.67% | 28.04s |
| 9 | 630.90 | 11.86% | 27.54s |
| 10 | 720.6 | 27.77% | 28.06s |
根据上述十次测试结果可以得出
最好解:
路径长度为630.90,参考最优解为564,误差为11.86%。
最差解:
路径长度为726.87,参考最优解为564,误差为28.88%。
平均值:
路径长度为695.71,参考最优解为564,误差为23.35%
标准差:
33.164
方差:
1099.86
算法的平均速度:
运行时间为28.587s
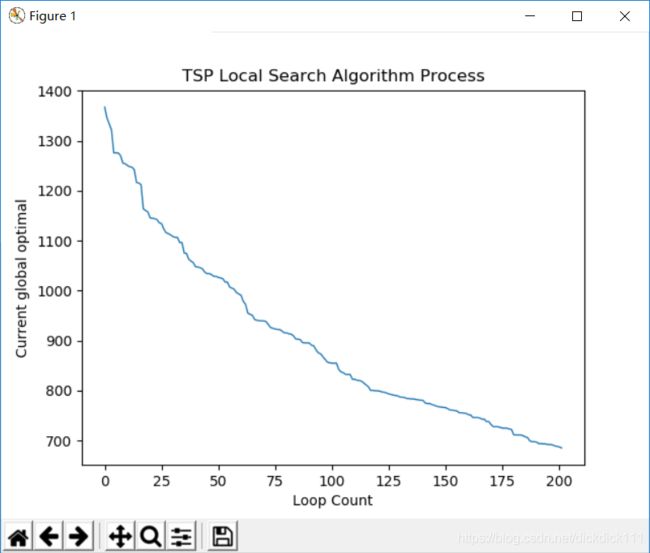
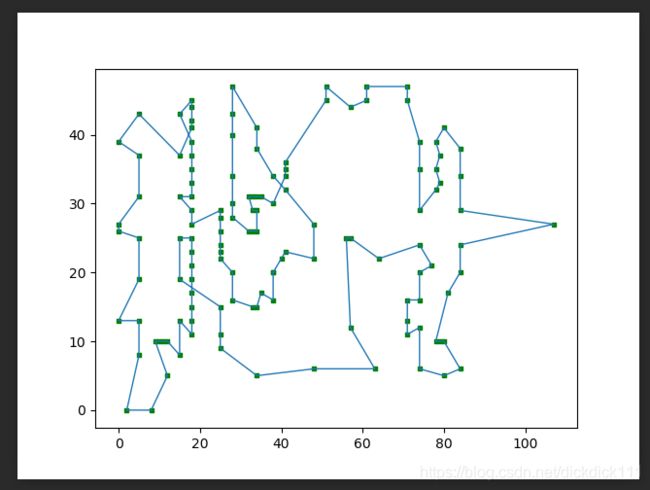
其中一次运行结果的解下降情况,横坐标是循环次数,纵坐标为当前的最优解
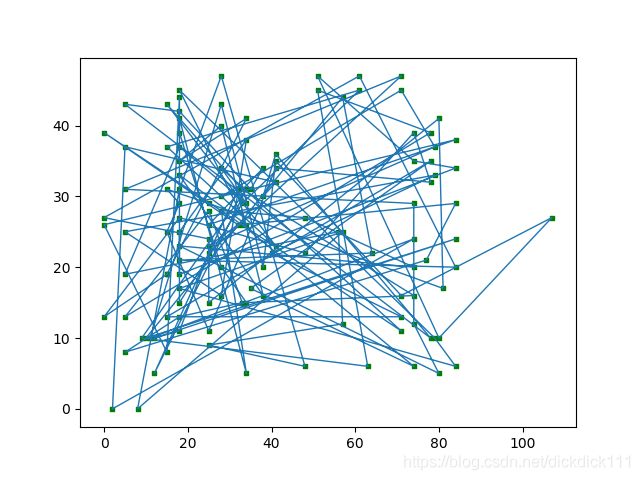
显示TSP路径的收敛情况
第一次循环:
最后一次循环:
明显看到其中的变化情况,最终解仍存在较多交叉情况,所得的最终解存在的误差仍比较大,故局部搜索算法不能很好找出最优解。
总结
通过上述十次实验可以看出,局部搜索算法求出的TSP最优解误差较大,平均误差在23.35%,但是算法的运算时间较少,收敛速度较快。故需要一些不太精确的近似解时,可以利用局部搜索的方法来寻找。
b.模拟退火算法的结果
结果图表展示:
| 次数 | 最优解 | 误差 | 运行时间 |
|---|---|---|---|
| 1 | 604.66 | 7.21% | 140.95s |
| 2 | 588.93 | 4.42% | 141.38s |
| 3 | 603.82 | 7.06% | 141.50s |
| 4 | 604.40 | 7.16% | 140.69s |
| 5 | 584.39 | 3.61% | 140.74s |
| 6 | 590.22 | 4.64% | 146.57s |
| 7 | 602.10 | 6.74% | 137.56s |
| 8 | 594.34 | 5.32% | 141.66s |
| 9 | 597.50 | 5.85% | 139.20s |
| 10 | 600.23 | 6.42% | 142.35s |
根据上述十次测试结果可以得出
最好解:
路径长度为584.386,参考最优解为564,误差为3.61%。
最差解:
路径长度为604.66,参考最优解为564,误差为7.21%。
平均值:
路径长度为597.06,参考最优解为564,误差为5.86%
标准差:
7.26
方差:
52.65
算法的平均速度:
运行时间为141.26s
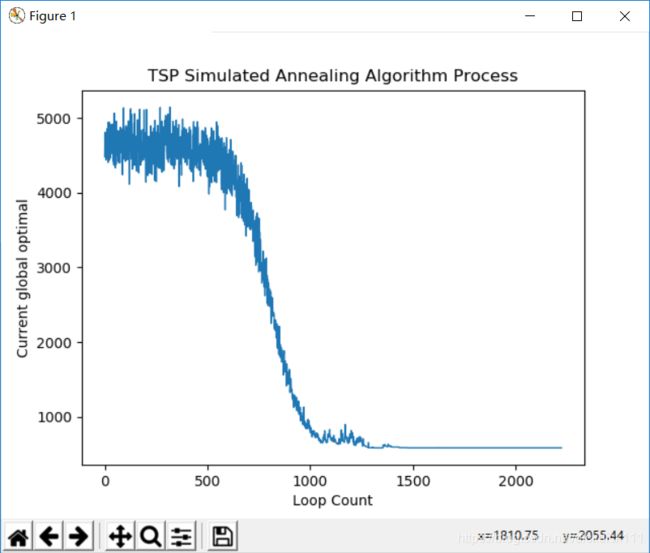
其中一次运行结果的解下降情况,横坐标是循环次数,纵坐标为当前的最优解
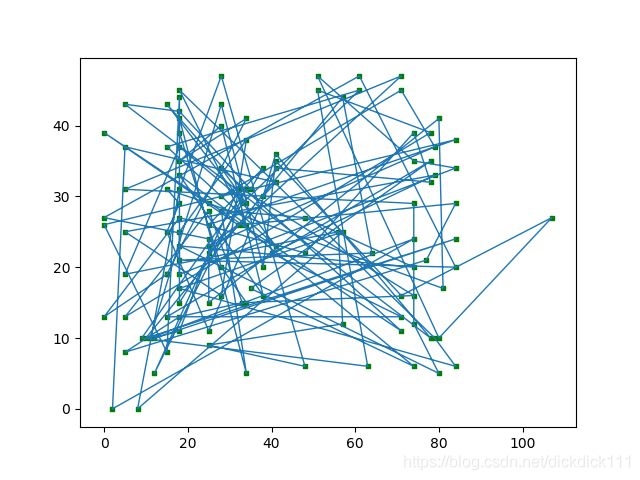
显示TSP路径的收敛情况
第一次循环:
最后一次循环:
明显看到其中的变化情况,图中已经较少交叉,找到较好的路径解。
总结
通过上述十次实验可以看出,模拟退火比局部搜索能找到更加精确的解,误差在5%到10%之间,但是使用的时间会更多,因为模拟退火在每一个温度都进行了相当多次的局部搜索,通过概率接受差解来跳出局部最优,达到更高的精度。
4. 结论
摸拟退火算法是基于随机搜索的,即在解的空间中展开随机搜索的。当问题的空间很大,而可行解比较多,并且对解的精度要求不高时,随机搜索是很有效的解决办法,因为其他的做法在这个时候时空效率不能让人满意。而借助演化思想和群集智能思想改进过的随机算法更是对解的分布有规律的复杂问题有良好的效果。
所谓退火是冶金专家为了达到某些特种晶体结构重复将金属加热或冷却的过程,该过程的控制参数为温度T。模拟退火法的基本思想是:在系统朝着能量减小的趋势这样一个变化过程中,偶尔允许系统跳到能量较高的状态,以避开局部极小点,最终稳定达到全局最小点。可以看到模拟退火不是单纯的采用贪心策略,它每获得一个解,对于该解有两种做法:若该解为更优解,则100%采纳;若该解为劣解,以一定的概率采纳该解,也就是说可能丢弃,可能采纳。所以在模拟退火算法的随机搜索过程中,当前的采纳解是时好时坏,呈现出一种不断波动的情况,但在总体的过程中又朝着最优的方向收敛。
利用模拟退火方法能较好的解决TSP问题,调整退火速度,初温,接受温度等参数可以控制到解的精度达到自己的满意范围内。除此之外,一些好的局部搜索方法也能加快找到最优解的速度,我们在一开始的实验只使用了单个局部搜索策略,误差范围大于10%。后来,经过老师的提醒,添加了多种搜索方法后,误差能很容易下降到10%以内。
5. 主要参考文献
- [人工智能]模拟退火算法及实践
- Simulated annealing —— Wiki
- 模拟退火算法参考博客