jzoj4196. 二分图计数

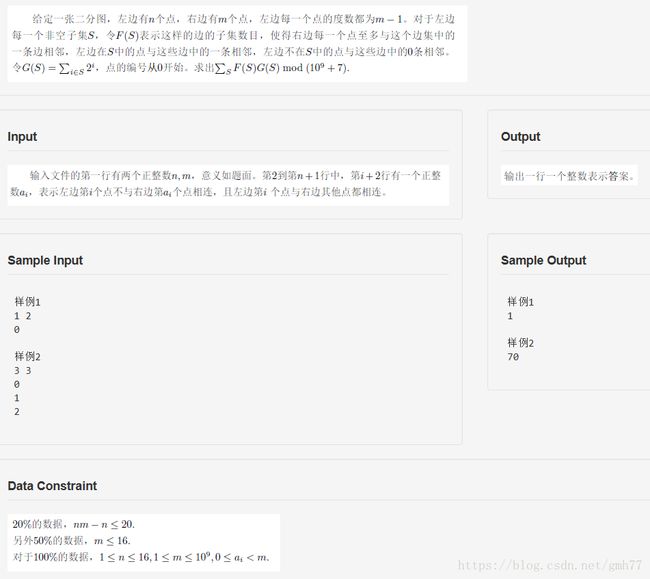
题目描述

70%

看到这种限制条件特别少的题目，首先考虑用容斥来解
（然而我考试时就想到了但是每写出来）
我以为40min写容斥很充足

先枚举选了的点集i，之后在枚举这些点中那些选了不能选的
不能选的点被固定，之后从剩余的点数往下乘到(m-点集大小+1)
要预先处理出那些情况是不可能的，即选了的点不重复

乘积和状态中1的个数都可以预处理，所以复杂度是 O(22n) O ( 2 2 n )

100%

枚举一个i，之后j不断减一再&i
这样可以保证枚举的j一定合法

最终的总复杂度为 O(3n) O ( 3 n )
(实际每个点都考虑了3种情况，一共n个点)

code

#include 
#include 
#include 
#include 
#include 
#include 
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define mod 1000000007

using namespace std;

const int p[17]={0,1,2,4,8,16,32,64,128,256,512,1024,2048,4096,8192,16384,32768};

struct AA{int x,y;
} A[20];
int a[20];
long long Ans[65537];
int B[65537];
int _S[17][17];
bool bz[20];
bool Bz[65537];
long long n,m,i,j,k,l,N,L,ans,S,_L,I,x;

bool cmp(AA a,AA b) {return a.xvoid init(int t,int s)
{
    if (t>n)
    {
        Bz[s]=1;
        return;
    }

    init(t+1,s);
    if (!bz[a[t]])
    {
        bz[a[t]]=1;
        init(t+1,s|p[t]);
        bz[a[t]]=0;
    }
}


int main()
{
    freopen("bipartite.in","r",stdin);
    freopen("bipartite.out","w",stdout);

    memset(_S,255,sizeof(_S));

    scanf("%d%d",&n,&m);
    fo(i,1,n) scanf("%d",&A[i].x),A[i].x++,A[i].y=i;
    sort(A+1,A+n+1,cmp);

    j=0;
    fo(i,1,n)
    {
        j+=(A[i].x!=A[i-1].x);
        a[A[i].y]=j;
    }
    init(1,0);

    L=p[n]*2-1;
    fo(i,0,L)
    {
        k=i;
        while (k)
        {
            B[i]+=k&1;
            k>>=1;
        }
    }

    fo(i,0,L)
    {
        j=i;

        while (j>=0)
        {
            j&=i;

            if (Bz[j])
            {
                if (_S[B[i]][B[j]]>-1)
                S=_S[B[i]][B[j]];
                else
                {
                    S=1;
                    fo(k,m-B[i]+1,m-B[j])
                    S=S*k%mod;

                    _S[B[i]][B[j]]=S;
                }

                if (B[j]&1)
                Ans[i]=(Ans[i]-S)%mod;
                else
                Ans[i]=(Ans[i]+S)%mod;
            }

            j--;
        }
    }

    fo(i,0,L)
    ans=(ans+Ans[i]*i)%mod;

    if (ans<0) ans+=mod;
    printf("%lld\n",ans);

    fclose(stdin);
    fclose(stdout);
}