机器学习：对于反向传播算法(backpropagation)的理解以及python代码实现

本文是对机器学习中遇到的后向传播算法进行理解，假设读者已经知道神经网络中的神经元的含义，激励函数的定义，也知道了后向传播算法那个传播公式等。本文主要是为了理解为什么后向传播算法中的 δ 是安照那个传播方式往后传播。

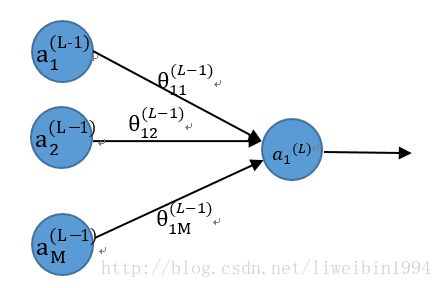
如上图，其中，L是神经网络的层数，a是神经元的输出， θ 是权重(参数)。
对于最后一层的神经元来说，偏差E我们可以很容易地定义：

E=12(a(L)1−y)2

所以对 θ(L−1)11 求偏导：

∂E∂θ(L−1)11=∂E∂a(L)1⋅∂a(L)1∂z(L)1⋅∂z(L)1∂θ(L−1)11

其中， z(L)1=a(L−1)1θ(L−1)11+a(L−1)2θ(L−1)12+...+a(L−1)Mθ(L−1)1M

在这里， δ(L)1=∂E∂a(L)1⋅∂a(L)1∂z(L)1

所以， ∂E∂θ(L−1)11=δ(L)1⋅∂z(L)1∂θ(L−1)11=δ(L)1⋅a(L−1)1

显然，由于我们知道了 a(L)1 ，所以我们很容易就可以得出结果，即：

∂E∂θ(L−1)11=(a(L)1−y)⋅a(L)1⋅(1−a(L)1)⋅a(L−1)1

现在，让我们往后一层来看。

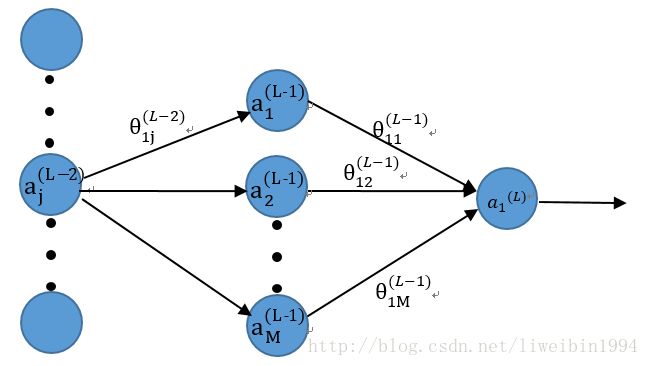
在这一层，我们要对 θ(L−2)1j 求偏导，则：

∂E∂θ(L−2)1j=∂E∂a(L−1)1⋅∂a(L−1)1∂z(L−1)1⋅∂z(L−1)1∂θ(L−2)1j

根据我们对 δ 的定义，上式也可以写为：

∂E∂θ(L−2)1j=δ(L−1)1⋅a(L−2)j

那么接下来我们的目标就是要求出 δ(L−1)1 。

δ(L−1)1=∂E∂z(L)1⋅∂z(L)1∂a(L−1)1⋅∂a(L−1)1∂z(L−1)1=∂E∂a(L)1⋅∂a(L)1∂z(L)1⋅∂z(L)1∂a(L−1)1⋅∂a(L−1)1∂z(L−1)1=δ(L)1⋅θ(L−1)11⋅a(L−1)1⋅(1−a(L−1)1)

这样我们就找到了 δ(L−1)1 与 δ(L)1 之间的关系了。同理，我们可以得到：

δ(L−1)1=δ(L)1⋅θ(L−1)12⋅a(L−1)1⋅(1−a(L−1)1)......δ(L−1)M=δ(L)1⋅θ(L−1)1M⋅a(L−1)1⋅(1−a(L−1)1)

以此类推，再往后一层：

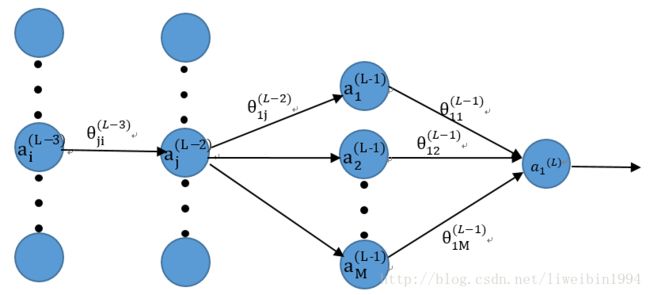
在这一层，我们要对 θ(L−3)ji 求偏导，则：

∂E∂θ(L−3)ji=∂E∂a(L−2)j⋅∂a(L−2)j∂z(L−2)j⋅∂z(L−2)j∂θ(L−3)ji=∑m∈M(∂E∂z(L−1)m⋅∂z(L−1)m∂a(L−2)j)⋅∂a(L−2)j∂z(L−2)j⋅∂z(L−2)j∂θ(L−3)ji=∑m∈M(∂E∂a(L−1)m⋅∂a(L−1)m∂z(L−1)m⋅θ(L−2)mj)⋅∂a(L−2)j∂z(L−2)j⋅∂z(L−2)j∂θ(L−3)ji=∑m∈M(δ(L−1)m⋅θ(L−2)mj)⋅∂a(L−2)j∂z(L−2)j⋅∂z(L−2)j∂θ(L−3)ji

所以，只要我们找到每一层的 δ 就可以算出偏导数了，而每一层 δ 都可以由后一层的 δ 算出。这样递归到了最后一层（输出层）。我们就可以找到任意一层的 δ 了。然后我们就可以算出 ∂E∂θ(l)ij

---

现在，让我们来考虑任意一层的情况了。

假设 a(l)∈R1×M(l) 为第 l 层的输出，其中 M(l) 是第 l 层的神经元个数。
所以，

∂E∂a(l)=δ(l+1)∗Θ(l)T

其中， Θ(l)∈RM(l)×M(l+1) 是第 l 层到第 l+1 层的权重参数矩阵。

δ(l+1)∈R1×M(l+1) 。

∗ 代表矩阵的乘法运算。

这样我们就得到了 ∂E∂a(l)∈R1×M(l) 。一般在代码中，它就是第 l 层的error，相当于输出层的E。

接下来我们要求 δ(l) 。

δ(l)=∂E∂a(l)⊙a(l)⊙(1−a(l))

其中， ⊙ 代表矩阵对应元素相乘。

最后，我们就可以求出第 l−1 层的权重参数矩阵的偏导数了。

∂E∂Θ(l−1)=a(l−1)T∗δ(l)

---

最后，我们用python实现一个简单的神经网络的训练。假设我们的训练集如下图所示：

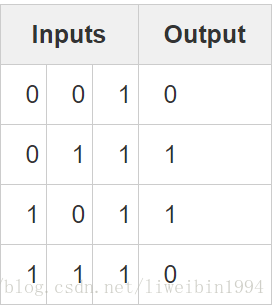
# -*- coding: utf-8
import numpy as np

# define sigmoid function
def nonlin(x,deriv=False):
    if(deriv==True):
        return x*(1-x)

    return 1/(1+np.exp(-x))


# input dataset 总共有4组输入
X = np.array([  [0,0,1],
                [0,1,1],
                [1,0,1],
                [1,1,1] ])

# output dataset 四组输出
y = np.array([[0,1,1,0]]).T

#seed random numbers to make calculation
np.random.seed(1)

# initialize weights randomly with mean 0
#theta0 是一个3*4的参数矩阵,输入层有3个输入节点(神经元)，隐藏层有4个节点(神经元)，所以参数是3*4d的矩阵
theta0 = 2*np.random.random((3,4)) - 1

#theta1是一个4*1的参数矩阵，隐藏层有4个节点(神经元)，输出层有1个节点(神经元)
theta1 = 2*np.random.random((4,1)) - 1

for j in xrange(60000):
    a0 = X  #a0表示第一层(输入层)，a0的每一行表示一组输入数据
    a1 = nonlin(np.dot(a0,theta0)) #a0与theta0的相乘得到的就是z1，经过sigmod函数就是a1了。a1是4*4的矩阵。注意是批量运算，a1的每一行代表一组训练数据。
    a2 = nonlin(np.dot(a1,theta1)) #跟上一个语句一样的道理,a2是一个4*1的矩阵，每一行代表一组训练数据

    E = y - a2 #获得偏差E，4*1的矩阵，每一行代表一组训练数据

    if (j% 10000) == 0:
        print "Error:" + str(np.mean(np.abs(E)))

    a2_delta = E*nonlin(a2,deriv=True) #这才是点乘，对应元素相乘，a2_delta是一个4*1的矩阵，每一行代表一组训练数据
    a1_error = a2_delta.dot(theta1.T) # a1__error其实就是偏差对a1求偏导对应输出层的E，也是每一行代表一组训练数据
    a1_delta = a1_error*nonlin(a1,deriv=True)

    theta1 = theta1 + a1.T.dot(a2_delta)
    theta0 = theta0 + a0.T.dot(a1_delta)

print "output after training:"
print a2

代码参考自：http://iamtrask.github.io/2015/07/12/basic-python-network/