2020牛客多校10：Identical Trees（树hash + 树同构 + 费用流模板）

---

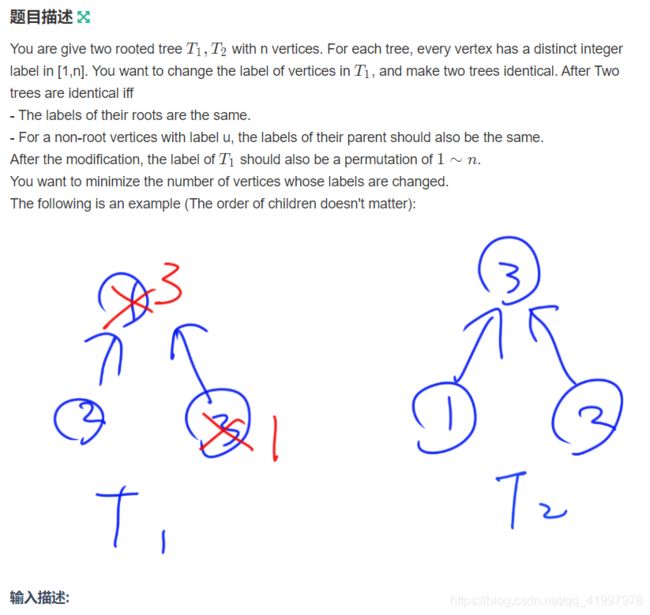
题意：给出两棵同构的有根树，同构修改点的标号使得两棵树完全一样，至少需要修改多少次。

分析：肯定是将子树和另外一棵的某个子树对应，而两棵子树的问题是一个子问题，显然只有同构的子树才可以对应，这要用到 树hash 来判断同构。

树hash 形如：$hash[u]=\sum _{v\in son[u]}hash[v]\ast prime[son\_size[v]]+1$，通过 hash 值可以在不管标号的情况下唯一确定一棵树的形态。

转移显然是一个匹配问题，要使得匹配后代价和最小，可以用最小费用最大流。

注：如果求解的是两棵同构子树最少需要修改的次数使得他们相同，只能过94%，如果求解的是两棵同构子树最多相同的部分，才可以 AC

---

代码：

#include 
#include 
#include 
#define M 505
#define inf 0x3f3f3f3f
#define pii pair
#define fir first
#define sec second
typedef long long ll;
const int maxn = 1010;
const int mod = 998244353;
using namespace std;
bool ispri[maxn * 10];
int pri[maxn * 10], n, dp[maxn][maxn], s, t;
struct MCMF {
     
	struct node{
     
		int v,c,w,rev;		//rev 是 反向弧(u,v)，v 在 u 的位置。
		node(int vi = 0,int ci = 0,int wi = 0,int ri = 0) {
     
			v = vi;c = ci;w = wi;rev = ri;
		}
	};
	int dis[maxn],h[maxn],preV[maxn],preE[maxn];
	vector<node> g[maxn];
	vector<int> pot;			//点集 
	void init() {
     
		for(int i = 0; i < maxn; i++) g[i].clear();
	}
	void clear() {
     
		for (auto it : pot)
			g[it].clear(), h[it] = preV[it] = preE[it] = 0;
		pot.clear();
	}
	void add(int u,int v,int c,int w) {
     
		g[u].push_back(node(v,c,w,(int)g[v].size()));
		g[v].push_back(node(u,0,-w,(int)(g[u].size() - 1)));
	}
	int maxflow(int s,int t,int flow = inf) {
     
		int ans = 0,f = 0;
		/*fill(h,h + t + 1,0);
		fill(preV,preV + t + 1,0);
		fill(preE,preE + t + 1,0);*/
		while(flow) {
     
			priority_queue<pii,vector<pii>,greater<pii> > q;
			for (auto it : pot)
				dis[it] = inf;	
		//	fill(dis,dis + t + 1,inf);
			dis[s] = 0;q.push(pii(dis[s],s));
			while(!q.empty()) {
     
				pii now = q.top();
				q.pop();
				int u = now.sec;
				if(dis[u] < now.fir) continue;
				for(int i = 0; i < g[u].size(); i++) {
     
					int v = g[u][i].v,c = g[u][i].c,w = g[u][i].w;
					if(c && dis[v] > w + dis[u] + h[u] - h[v]) {
     
						preV[v] = u;preE[v] = i;
						dis[v] = w + dis[u] + h[u] - h[v];
						q.push(pii(dis[v],v));
					}
				}
			}		
			if(dis[t] == inf) break;	
			for (auto it : pot)	h[it] += dis[it];
			//for(int i = 0; i <= t + 1; i++) h[i] += dis[i];
			int mx = inf;
			for(int i = t; i != s; i = preV[i])
				mx = min(mx,g[preV[i]][preE[i]].c);
			flow -= mx; f += mx; ans += h[t] * mx;
			for(int i = t; i != s; i = preV[i]) {
     
				g[preV[i]][preE[i]].c -= mx;
				g[i][g[preV[i]][preE[i]].rev].c += mx;
			}
		}
		return -ans;
	}	
} p;
struct tree {
     
	vector<int>	g[maxn];
	int son[maxn], val[maxn], root;
	void add(int u,int v) {
     
		g[u].push_back(v);
	}
	void dfs(int u) {
     
		son[u] = 1; val[u] = 1;
		for (auto it : g[u]) {
     
			dfs(it);
			son[u] += son[it];
			val[u] = (val[u] + 1ll * val[it] * pri[son[it]] % mod) % mod;
		}
	}
} T[2];
void sieve(int n) {
     
	ispri[1] = ispri[0] = true;
	pri[0] = 0;
	for (int i = 2; i <= n; i++) {
     
		if (!ispri[i])
			pri[++pri[0]] = i;
		for (int j = 1; j <= pri[0] && i * pri[j] <= n; j++) {
     
			ispri[i * pri[j]] = true;
			if (i % pri[j] == 0) break;
		}
	}
}
int solve(int i,int j) {
     
	for (auto x : T[0].g[i]) {
     
		for (auto y : T[1].g[j]) {
     
			if (T[0].val[x] == T[1].val[y])
				dp[x][y] = solve(x,y);
		}
	}
	for (auto x : T[0].g[i])
		p.add(s,x,1,0), p.pot.push_back(x);
	for (auto y : T[1].g[j])
		p.add(n + y,t,1,0), p.pot.push_back(n + y);
	for (auto x : T[0].g[i]) {
     
		for (auto y : T[1].g[j]) {
     
			if (T[0].val[x] == T[1].val[y])
				p.add(x,n + y,1,-dp[x][y]);
		}
	}
	p.pot.push_back(s);
	p.pot.push_back(t);
	int ans = p.maxflow(s,t) + (i == j);
	p.clear();
 	return ans;
}
int main () {
     
	sieve(5000);
	scanf("%d",&n);
	s = 2 * n + 2, t = 2 * n + 1;
	for (int i = 1, f; i <= n; i++) {
     
		scanf("%d",&f);
		if (f == 0) T[0].root = i;
		else T[0].add(f,i);
	}
	for (int i = 1, f; i <= n; i++) {
     
		scanf("%d",&f);
		if (f == 0) T[1].root = i;
		else T[1].add(f,i);
	}
	T[0].dfs(T[0].root);
	T[1].dfs(T[1].root);
	printf("%d\n",n - solve(T[0].root,T[1].root));
    return 0;
}