第五章——挖掘建模之决策树

决策树

概念
决策树方法在分类、预测、规则提取等领域有着广泛应用。
构造决策树的核心问题是在每一步如何选择适当的属性对样本做拆分。对一个分类问题，从已知类标记的训练样本中学习并构造出决策树是一个自上而下，分而治之的过程。

构造
决策树是一种树形结构，其中每个内部节点表示一个属性上的测试，每个分支代表一个测试输出，每个叶节点代表一种类别。
形如下图:
决策树算法的分类

决策树算法	算法描述
ID3算法	其核心是在决策树的各级节点上，使用信息增益方法作为属性的选择标准，来帮助确定生成每个节点时所采用的合适属性
C4.5算法	C4.5决策树生成算法相对于ID3算法的重要改进是使用信息增益率来选择节点属性。C4.5算法可以克服ID3算法存在的不足：ID3算法只适用于离散的描述属性，而C4.5算法既能够处理离散的描述属性，也可以处理连续的变量属性
CART算法	CART决策树是一种十分有效的非参数分类和回归方法，通过构建树、修剪树、评估树来构建一个二叉树。当终结点是连续变量时，该树为回归树；当终结点是分类变量，该树为分类树

详细介绍ID3算法

信息增益
设S是s个数据样本的集合。假定类别属性具有m个不同的值: $C_i$(i=1,2,…,m)。设$s_i$是类$C_i$中的样本数对一个给定的样本，它总的信息熵为
$I(s_1,s_2,...,s_m)=\sum _{i=1}^m{P}_{i}lo{g}_2(P_i)$ ————————(1)
其中，$P_i$是任意样本属于$C_i$的概率，一般可以用$\frac{s_i}{s}$估计
根据属性A(具有k个不同的值)划分样本的信息熵值为
$E(A)=\sum _{j=1}^k\frac{s_{1j}+s_{2j}+...+s_{mj}}{s}I(s_{1j},s_{2j},...,s_{mj})$————————(2)
其中$I(s_{1j},s_{2j},...,s_{mj})=-\sum _{i=1}^m{P}_{ij}lo{g}_2(P_{ij})$,
$P_{ij}=\frac{s_{ij}}{s_{1j}+s_{2j}+...+s_{mj}}$是子集$S_j$中类别为$C_i$的样本概率。
最后，用属性A划分样本集S后所得的信息增益(Gain)为
$Gain(A)=I(s_1,s_2,...,s_m)-E(A)$————————(3)

ID3算法算法流程

1. 对当前样本集合，计算所有属性的信息增益；
2. 选择信息增益最大的属性作为测试集，把测试属性取值相同的样本划分为同一个子集样本集；
3. 若子样本集的类别属性只含有单个属性，则分支为叶子节点，判断其属性值并标上相应的符号，然后返回调用处；否则对子样本集递归调用本算法。

编写代码计算信息增益
数据如下(部分)

在编写代码之前，我们先对数据集进行属性标注。

天气：0代表坏，1代表好；
是否周末：0代表否，1代表是；
是否有促销：0代表否，1代表是；
销售：no代表低，yes代表高。

计算总的信息熵

# -*- coding:utf-8 -*-
from math import log
import pandas as pd
import warnings

warnings.filterwarnings('ignore')

data = pd.read_excel('../data/5-2 sales_data.xls')

data['天气'] = data['天气'].map({
    '好': 1,
    '坏': 0
})
data['是否周末'] = data['是否周末'].map({
    '是': 1,
    '否': 0
})
data['是否有促销'] = data['是否有促销'].map({
    '是': 1,
    '否': 0
})
# 将数据转化成二维列表
dataSet = data.values.tolist()
# 特征列
labels = ['天气', '是否周末', '否有促销']


def IShannon(dataSet):
    # 计算数据的总数
    numcounts = len(dataSet)
    # 记录每个标签出现的次数
    labelCounts = {}
    # 对每组特征向量进行统计
    for feature in dataSet:
        featureLabel = feature[-1]  # 最后一列为标签列
        if featureLabel not in labelCounts.keys():  # 添加新统计到的标签，并计数
            labelCounts[featureLabel] = 0
        labelCounts[featureLabel] += 1  # label计数

    Ientropy = 0.0  # 信息熵
    # 计算信息熵
    for counts in labelCounts:
        counts = counts
        P = float(labelCounts[counts]) / numcounts  # 选择该标签的概率
        Ientropy -= P * log(P, 2)  # 利用公式计算
    return Ientropy  # 返回信息熵


# main函数
if __name__ == '__main__':
    print(IShannon(dataSet))

计算结果如下图：

计算信息增益

# 计算每个特征的信息熵
def splitDataSet(dataSet, axis, value):
    """
    :param dataSet: 待划分的数据集
    :param axis: 划分数据集的特征的维度
    :param value: 特征的值
    :return: 符合该特征的所有实例
    """
    retDataSet = []
    for featVec in dataSet:
        if featVec[axis] == value:
            reducedFeatVec = featVec[:axis]  # 删掉这一维特征
            reducedFeatVec.extend(featVec[axis + 1:])
            retDataSet.append(reducedFeatVec)
    return retDataSet


def chooseBestFeatureToSplit(dataSet):
    # 特征数量, 最后一列是标签
    numfeature = len(dataSet[0]) - 1
    # 计数数据集的信息熵
    baseEntropy = IShannon(dataSet)
    # 信息增益
    Gain = 0.0
    # 最优特征的索引值
    bestFeature = -1
    # 遍历所有特征
    for i in range(numfeature):
        # 获取dataSet的第i个所有特征
        featList = [example[i] for example in dataSet]
        # 创建set集合{}，元素不可重复
        uniqueVals = set(featList)
        # 条件信息熵
        newEntropy = 0.0
        # 计算信息增益
        for value in uniqueVals:
            # subDataSet划分后的子集
            subDataSet = splitDataSet(dataSet, i, value)
            # 计算子集的概率
            prob = len(subDataSet) / float(len(dataSet))
            # 根据公式计算条件信息熵
            newEntropy += prob * IShannon((subDataSet))
        # 信息增益
        infoGain = baseEntropy - newEntropy
        # 计算信息增益
        if (infoGain > Gain):
            # 更新信息增益，找到最大的信息增益
            Gain = infoGain
            # 记录信息增益最大的特征的索引值
            bestFeature = i+2
            # 返回信息增益最大特征的索引值
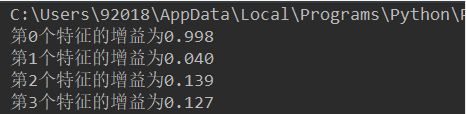
    return bestFeature

运行结果如下：

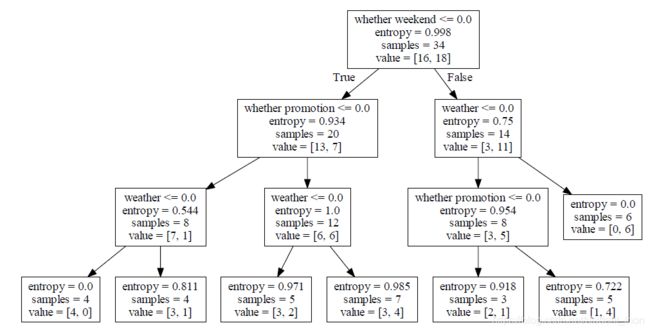
画决策树

import pandas as pd
filename = '../data/5-2 sales_data.xls'
data = pd.read_excel(filename, index_col=u'序号')

# 数据是类别标签，要将它转化为数据
# 用1来表示“好”“是”“高”这三个属性，用-1表示“坏”“否”“低”
# data == u'好' # 数组转换为bool类型
# data[data == u'是']  # 用布尔类型数组来取data的值
data[data == u'好'] = 1
data[data == u'是'] = 1
data[data == u'高'] = 1
data.columns = ['序号', 'weather', 'whether weekend', 'whether promotion']
data[data != 1] = -1
x = data.iloc[:, :3].astype(int)
y = data.iloc[:, 3].astype(int)

from sklearn.tree import DecisionTreeClassifier as DTC
# 建立决策树模型，基于信息熵
dtc = DTC(criterion='entropy')
dtc.fit(x, y)

# 导入相关函数，可视化决策树
# 导出的结果一个dot文件，需要安装Graphviz才能将它转换为pdf或png格式
from sklearn.tree import export_graphviz
with open("tree.dot", 'w') as f:
    f = export_graphviz(dtc, feature_names=['weather', 'whether weekend', 'whether promotion'], out_file=f)

此时文件中会产生tree.dot文件

再在终端命令中输入

dot -Tpdf tree.dot -o tree.pdf

就会生成pdf文件，能看到所构造的决策树模型了

注意
我在看书写代码的过程中有遇到过如下几个问题:
解决办法

将红色箭头所指向的这块代码(原书所写)修改为

在Pycharm中，生成的文件尽量不要包含中文，不然会出现乱码不太容易修改