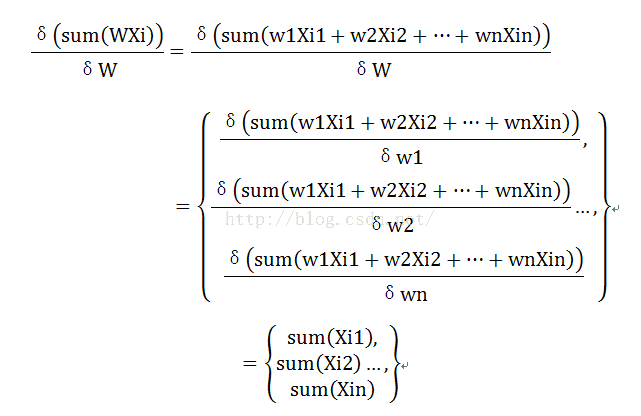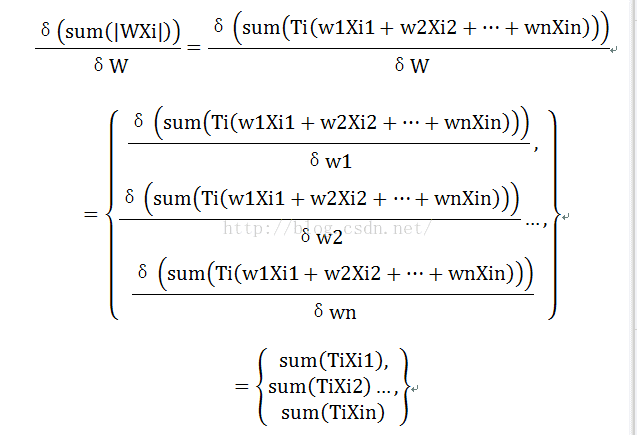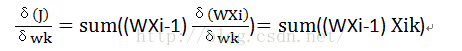线性判别函数

最近看到线性判别分析LDA，然后发现网上有少量的文章说线性判别函数和LDA很相似，当时就感觉虽然名字很像，但这完全是两个不相关的模型。所以就把这些东西详细地区别了一下。

一、线性判别函数

1、函数是对模式进行分类的准则函数，因此非常明显线性判别函数是用来进行模式识别的。若分属于ω1，ω2的两类模式可用一方程d(X) =0来划分，那么称d(X) 为判别函数，或称判决函数、决策函数。

例：一个二维的两类判别问题，模式分布如图示，这些分属于ω1，ω2两类的模式可用一直线方程d(X)=0来划分。d( X) = w1 x1 + w2 x2 +w3 = 0，式中x1 , x2 为坐标变量，w1 , w2, w3 为方程参数。

将某一未知模式 X代入：d( X) ，若d( X)>0，则属于ω1类，若d( X)<0，则属于ω2类。若d( X)=0，则可以考虑拒绝或者做出其他判断。判别函数d(X)可以是线性的或者非线性的函数，我们只讨论线性的，对于非线性的问题在广义线性判别函数的时候会将所有非线性的问题转换为线性问题。

在上面的例子中，我们讨论的是在一个二维的平面内进行分类，其实在大多时候数据的维度都远远的要超过二维。特别是在线性函数无法分割数据的时候往往需要把数据扩展到更高维度，才能用线性函数进行分割。

d( X) = w1 x1 + w2 x2 + …+wn xn+w0，X=[x1,x2,…,xn,1]，参数向量W=[w1,w2,…,wn,w0]

当有两类的时候用一个判别函数d1(X)即可实现分类，但是对于多类的情况，有三种划分方式：两分法，两分法， 两分法特例。

2、 两法用线性判别函数将属于ωi类的模式与其余不属于ωi类的模式分开此法将 M个多类问题分成M个两类问题，识别每一类均需M个判别函数。识别出所有的M类仍是这M个函数。

（1.1式）

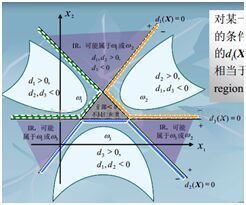
考虑所有的情况，发现上式中并没有考虑所有的情况，比如没有考虑到所有的判别式都为小于零的情况，和多个判别函数同时大于零的情况。下图考虑了分为三类的时候，可能出现的情况。

比如当有M类的时候，如果每条判别函数相互不平行而且交点至今没有重合，X所在的n维空间会被分成（m+1）m/2+1个区域，而只有m个区域里面的点才能满足1.1式，而剩下的（m+1）m/2+1-m个区域都无法进行明确的分类。这也是目前存在的问题。

3、两分法，一个判别界面只能分开两类，不能把其余所有的类都分开，判决函数为dij( X)=WijX，这里dij=-dji。判别函数的性质dij(X)>0,对所有的j=1…m，若x属于第i类。这种方法一共需要（m+1）m/2个判别式。

4、两分法特例，当ωi /ωj两分法中的判别函数dij(X) ，可以定义为dij ( X) = di (X)- d j(X)时，那么di(X)>dj(X)就相当于多类情况2中的dij(X) >0。此时有m个判别函数di(X)=WiX。判别函数的性质为：di (X)=max{dk(X) k=1…m},若X属于第i类。可以通过dij ( X) = di (X)- d j(X)发现，这种分类方法只不过是第二种分类方法的特例，如果这种分类方法可分则第二种分类方法必定可分，如果第二种分类方法可分，这种方法未必可分。

二、广义线性判别函数

在上面曾经提到低维空间的非线性问题可以在高维空间变成线性问题。上面讲的所有都是在X所在的空间中线性可分为前提条件，是因为即使原始数据D在原来空间线性不可分，我们只需要把低维空间的D扩展到高维空间的X就线性可分了。下面举两个例子：

 

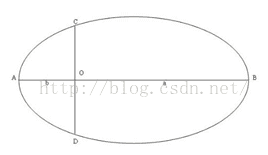
比如在二维平面内需要一个正玄曲线y-sin(X)=0才能将数据准确的分割为两类。此时数据D=(x,y),如果把数据扩展到更高维度的空间T，T=(x,y,sin(x),sin(y),1)，那么对于T空间的数据肯定可以找到w1x+w1y+w3(sin(X))+w4(sin(y))+w0=0这样一个线性表达式来使得数据可以划分。针对在二维空间需要椭圆曲线才能划分的数据只需要将D=(x,y)扩展到 T=(x,y,x^2,y^2,xy,1)空间，则在T所在的空间就可以将数据线性划分了。实际上在建模的时候首先要选定的就是要把原始的数据D怎样扩展到更高维度的空间，数据才能变得线性可分。这是建立模型的关键步骤。

三、判别式的求取方法

在上面介绍了模型，也就是建模的时候要做哪些工作。下面的工作就是解模了，这里介绍了三种求取判别式的方法。分别为感知器算法、梯度法、最小误差平方法。接下来介绍的三种方法都是以两类为例介绍的。

1、感知器算法

感知器算法算是一种最简单的算法了，基本上就是一种错了就改的思想，就像是教育小孩子对了的话就告诉他对了不用改正，错了的话就要向正确的方向改正一样。两类线性可分的模式类：w1，w2 ，线性判别函数d(X),若d(X)>0，则X属于w1，若d(X)<0，则X属于w2.首先将数据增加一个维度，所有数据在此维度上的值都是1。然后将属于w2类的数据全部乘上-1，这样处理后的样本记为X’，那么对于X’中的任意一组数据都应该满足d(X’)>0。感知器算法的步骤为：

第一步：选择N个分属于ω1和 ω2类的模式样本构成训练样本集{X1, …, XN}进行增广（扩展一个维度，所有数据在此维度上的值都为1）和规范化处理（上面所说的对于d(X)<0的情况，数据乘以-1的操作）。任取权向量初始值W(1)，开始迭代。迭代次数k=1 。

第二步：用全部训练样本进行一轮迭代，计算W (k)Xi的值，并修正权向量。分两种情况，更新权向量的值：若W (k)Xi≤ 0，分类器对第i个模式做了错误分类，权向量校正为：W(k +1) = W(k) + cXi，c为矫正增量为正值，这个值需要自己设定。若W (k)Xi> 0,表示分类正确则不需要改变权向量:W(k +1) = W(k)

统一写为：若W (k) Xi> 0，分类正确，权向量不变：W(k +1) = W(k)

W (k) Xi <= 0,分类错误，权向量改变：W(k +1) =W(k) + cXi

第三步：分析分类结果：只要有一个错误分类，回到第二步，直至对所有样本正确分类。

对于为什么在判断错的时候要做W(k +1)=W(k) + cXi这样的改变，W(k +1) Xi= W(k) Xi+c Xi^2,所以W(k +1) Xi> W(k)Xi，代表k+1次的权值在对Xi数据的分类情况有了改善。可以证明算法在模式类别线性可分的时候是收敛的。对于多类的问题感知器算法的基本思想还是不变的：错了就向好的方向改变，正确就不再改变。

2、梯度法

梯度法一般的规则就是定义损失函数，然后沿着梯度下降使得损失函数下降到极小值点。损失函数定义为J=0.5sum(|WXi|- WXi),当第一眼看到这个损失函数的时候会感到很诧异，因为里面有取绝对值的运算，这种运算是不可导的。下面的Xi代表第i组数据，Xik代表第i组数据的第k维，k=1…n。首先看

同理引入Ti表示的符号，则

所以最后的

 

权值改变公式为，为步长，就像感知器算法中的c。只需要如此不断的改变权值，直到权值无法改变即求得了结果。其实通过对比了前面的感知器算法和梯度法会发现，感知器算法每次读入一组数据就改变一次权值，而上面讲的梯度法是所有数据都输入之后，求得所有的 WXi才改变一次权值。严格地说，感知器算法也是梯度法的一种。梯度下降算法改变权值都是通过统一的公式进行调整的，不过我们往往可以控制的是多少组数据改变一次权值，有一组数据改变一次权值的，有所有数据全部输入改变一次权值的，还有介于两者之间的K组数据改变一次权值的。如果要详细了解权值的改变方式可以了解BP神经网络中权值具体改变的方法。不过一般都是设置为输入K组数据改变一次权值，因为像感知器算法那样，每一组数据都改变一次权值，损失函数不是严格梯度下降的，容易导致损失函数震荡。而像上面讲的那样把所有数据输入，求得所有的 WXi才改变一次权值，虽然这样在 足够小的理想前提条件下，损失函数会严格的下降，但是当训练数据量很大的时候会造成权值改变速度过慢。所以一般采取折中的方式选择输入K组数据改变一次权值，在机器学习中batchsize一般表示K。

3、最小误差平方法

当把这个方法写出来的时候，感觉这样写好不准确，因为这种方法其实还是梯度下降法，回想当分成两类的时候，要求的这样的一个W，使得满足WXi>0,i=1…，也就是对所有的Xi都要满足WXi>0。既然我们要满足这么一个条件，那么WXi=C>0,是不是也恒定满足这样的条件呢，C代表随便一个正的常数。比如C=1的时候，只需要求WXi=1的解即可，求得W必定满足WXi>0，因为WXi=1。所有此时转换为对方程组的求解了，但是实际问题并不像我们想的那样简单，为什么？因为我们求解的参数个数可能远小于方程组的个数，很有可能根本没有解，因为样本的数量远大于样本的维度再正常不过了。所以还是通过定义损失函数来进行求解最好不过，定义损失函数为J=0.5sum((WXi-1)^2),这时候有人会想C为什么要等于1，而不是等于其他常数，其实很简单，C等于任意一个正整数求得的结果都是一样的，WXi=1求得W记为W(1)，WXi=2求得W记为W(2)，易知W(2)=2 W(1)，所以C无论选取为哪一个正的常数都无所谓，求得的结果都会满足WXi>0，而权向量W在方向上是不会变化的。

然后按照不断的迭代改变权值即可。

四、线性判别函数和SVM

通过看机器学习导论一书可以发现，线性判别函数和支撑向量机SVM放在了同一章节进行讲解了，可以发现线性判别函数和支撑向量机SVM是有很多相似的地方的。基本上都离不开线性这个地方，因为支撑向量机一直解决的问题就是在一个线性可分的空间，如何求出一个超平面将数据最好的分开，注意最好这两个字，而线性判别函数所做的是在一个线性可分的空间，如何求出一个超平面将数据分开。SVM比线性判别函数多了最好两个字，因而就相比之下比线性判别函数的求解复杂了好多，看了那么多关于SVM的资料，感觉最好的就是coursera上面台大林轩田老师开设的机器学习课程。这两个模型基本的思想都是在一个低维空间线性不可分的时候，先把低维空间扩展到高维空间，线性判别函数是是找一个分类超平面，而SVM是找一个最好的分类超平面。