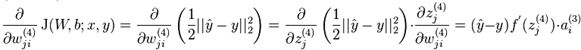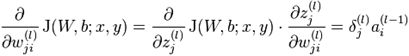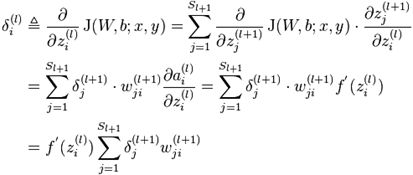[本文链接:http://www.cnblogs.com/breezedeus/archive/2013/04/22/3036050.html,转载请注明出处]
神经网络模型通常被用于做有监督学习(如分类,回归等情景),本文主要介绍下神经网络模型中使用后项传播算法(Backpropagation)来计算梯度的方法。下图是一个四层神经网络模型的图表示,其中第一层(L1)是输入层,第四层(L4)是输出层,中间两层通常被称为隐藏层。
这里我们复用了[1]中的记号,具体记号的含义请参考[1](注:[1]和[2]中关于z和a的定义刚好反过来了)。具体的模型如下:
其中f()为activation function,通常取为sigmoid函数:
或者hyperbolic tangent函数:
注意我们之前的模型表达顺序刚好是对应图表示里从左到右的顺序,在有一个样本点(x, y),我们可以按照此顺序获得对y的预测值(当然,是假定模型参数W和b都已知道)。这个过程通常被称为forward propagation。
求解模型中的参数W和b通常是通过最优化方法(如梯度下降、拟牛顿法等)最小化某个给定的目标函数获得的。在使用这些优化算法求解时,都需要计算目标函数对参数的梯度值。而通常目标函数的定义是各个训练样本点的误差之和,如在回归问题中,常用的目标函数是L2-Loss:
我们下面以此L2-Loss为例,说明求梯度的方法。
既然总目标函数值是各个训练样本点对应的目标函数值之和,他们对参数的梯度也有同样的关系。所以下面我只说明如何算对一个训练点![]() ,为简单考虑,我们略去上标(i),只写为(x, y)。先来看看对
,为简单考虑,我们略去上标(i),只写为(x, y)。先来看看对![]() 的偏导数:
的偏导数:
为简单起见,我们引入一个新定义:
那么前面的式子可以写为:
对于不同层的w,其偏导数都具有这样的格式:
其中l = 4, 3, 2。而![]() 。
。
既然![]() 在forward propagation中已经计算出来,只要我们能计算出所有层的
在forward propagation中已经计算出来,只要我们能计算出所有层的![]() ,那么对所有层的参数w的导数也就获得了。而对参数
,那么对所有层的参数w的导数也就获得了。而对参数![]() 的导数则等于
的导数则等于![]() 。
。
前面,我们已经知道![]() 。那么,现在的问题就是如何计算更低层的
。那么,现在的问题就是如何计算更低层的![]() ?下面我们将利用数学里求导数的链式法则,通过后一层的
?下面我们将利用数学里求导数的链式法则,通过后一层的![]() 计算出前一层的
计算出前一层的![]() 。这个从后往前计算
。这个从后往前计算![]() 和参数偏导数的过程通常被称为Back propagation。
和参数偏导数的过程通常被称为Back propagation。
其中l = 3, 2。虽然这个推到公式看起来有点恐怖,但其实只是把原来表达为![]() 的函数的目标值J(W, b; x, y)转换为使用
的函数的目标值J(W, b; x, y)转换为使用![]() 表达而已。比如,J(w, b; x, y),可以写成:
表达而已。比如,J(w, b; x, y),可以写成:
也可以写成:
详细的算法可见[1]或者[2]。
[References]
[1] Andrew Ng, Jiquan Ngiam et al. UFLDL Tutorial: Feature Learning and Deep Learning.
[2] Christopher Bishop. Chapter 5 Neural Networks, Pattern Recognition and Machine Learning, 2007.