身高、体重、脚长三个数值足以判断一个人的性别?贝叶斯分类模型
你的信用评分是高还是低?你在某个App上的活跃度怎么样?你是什么兴趣类型的用户?
每个商家对我们的信息了如指掌,几乎可以做到精准推荐,这一点都不奇怪,因为用户被商家建立的分类模型分类了无数次。商家通过我们的信息和行为留下的痕迹对我们进行分类,并且随着我们在商家那里留下的行为痕迹越来越多,分类结果会被自动更新,最后模型越来越精确。
是什么神通广大的模型让商家对用户能进行准确分类呢?其中最简便也应用最广泛的一个模型就是朴素贝叶斯分类(以下简称贝叶斯分类)。贝叶斯分类因为具有简单、准确率高、速度快的特点而被运用到很多大型数据库中。
什么是贝叶斯分类?
谈到贝叶斯分类,不得不提及三个概念:条件概率、后验概率、全概率公式。下面用体育比赛中的东道主效应为例说明这三个概念的含义。
美国心理学家Coumeya总结了棒球、足球、篮球等一些运动项目的主场胜率,发现主场明显高于客场:在主客场比赛场次对等情况下,主队在竞赛中获胜的比例超过50%。
如果已知在历届世界杯中,德国队赢得冠军的概率是37%,某一年德国队得到世界杯主办权的概率是60%。此时如果德国得到世界杯主办权,那么德国队赢得冠军的概率应该超过37%,因为这时德国队赢得冠军的事件(记为事件A)是在德国获得世界杯主办权事件(记为事件B)发生的情况下发生的,而世界杯比赛有东道主效应,有利于东道主夺得冠军。
在上述世界杯的例子中:
(1)事件A在事件B发生或不发生条件下的概率,事件B在事件A发生或不发生条件下的概率,都可以称为条件概率。条件概率中,只要存在两个事件,两个事件可以互为条件。
记A、B分别为事件,B事件分为B1、B2、B3…B10种情况,则:
条件概率(贝叶斯)公式:P(A|B)*P(B)=P(B|A)*P(A)
(2)事件A在事件B已经发生的条件下发生的概率就是后验概率。
正是因为后验概率的应用,让我们可以根据新出现的信息,改变对已有结果推测的准确性。贝叶斯概率也因此在数据分析、人工智能方面持续发光发热。
(3)事件A在事件B发生条件下发生的概率,记为P(A|B);在事件B不发生条件下的概率记为P(A|~B),则P(A)= P(A|B)+ P(A|~B)。在事件B有n种情况时,可拓展为:
全概率公式:P(A|B)=P(A|B1)+P(A|B2)+P(A|B3)+…+P(A|Bn)
有了条件概率、后验概率和全概率公式,我们就可以进行贝叶斯分类了。
如何进行贝叶斯分类?
贝叶斯分类适合预测结果为离散且可穷举的类型,如等级评分(A,B,C)、是否赢得比赛、是否结婚、是否违约等。
贝叶斯分类模型是根据计算得到的每一个类别的概率确定被分类的对象属于哪个类型,将对象划归到概率最大的类型中。所以贝叶斯分类的主要工作就是计算概率。
贝叶斯分类的主要步骤如下:
- 确定特征属性,并对特征属性取值划分
如:在根据身高、体重、脚长判断性别的例子中,特征属性可以确定为:身高、体重、脚长三个。
如果特征属性本身为类别型变量,则无需对特征属性取值进行划分;如果特征属性值为连续型变量,则需要对特征属性值进行区间划分,将连续的特征属性值变成类别型的特征属性值。
之所以对连续型特征属性值进行区间划分,是因为连续型变量取值无限多的特点与贝叶斯分类统计值出现的频率和预测结果仅要求划分少数类别的特点不一致。连续型变量可以有无限多个取值,而贝叶斯分类是根据每个特征属性值出现的频率预测概率。如果不将连续型变量转变为类别型变量,则基本上每个值都单独计数,最后计算的每个特征属性值出现的次数都很少,计算出的概率不准确。
注:尽量对连续型特征属性的取值进行归一化或标准化处理,然后就可以用统一的区间标准对特征属性的取值进行划分。具体的区间划分需根据实际情况设定,主要取决于取值区间对应的实际意义。
- 选取训练集和测试集,构建贝叶斯分类器
训练集和测试集必须有确定的类别,即要预测的结果。这里的类别划分一般是根据经验人工划分。训练集的样本一般在2000以上(可根据特征属性的多少,适当增加或减少训练集样本的数量)
(1) 计算训练集中各类别出现的概率;
(2) 计算训练集中各类别下各特征属性值出现的概率;
(3) 输入测试集各特征属性值,计算测试集各样本属于各个类别的概率,取值概率最大的类别即为个体所属的类别。
如:x1、x2、x3为某个体三个特征属性的取值,A,B为互斥的类别(除A、B外,没有其他类别)。若计算出
P(A|x1,x2,x3) = P(x1,x2,x3|A)*P(A)/(P(x1)*P(x2)*P(x3))= 0.6,
P(B|x1,x2,x3) = P(x1,x2,x3|B)*P(B/(P(x1)*P(x2)*P(x3)) =0.4,
则P(A|x1,x2,x3) > P(B|x1,x2,x3),可以判断该个体属于A类。
注:在实际模型计算中,可以省去分母特征属性值乘积(P(x1)*P(x2)*P(x3))的计算,因为分母相同,只需比较分子的大小即可;同时也可以减少计算复杂度,节省资源。
- 检验模型优劣:
比较通过模型预测的测试集分类结果与已知分类结果的差异,若差异在设定的误差范围内,则模型可以接受,并可通过将新预测的个体加入训练集逐渐扩大样本,对模型进行优化。
贝叶斯分类的R语言实现
预备步骤:
安装plyr程辑包,plyr程辑包有数据透视表的作用。
plyr包的主函数是**ply形式,第一个字母表示输入的数据格式,第二个字母表示输出的数据格式;首字母可以是(d、l、a),第二个字母可以是(d、l、a、_),d表示数据框,l表示列表,a表示数组,_表示没有输出。
代码如下:
library(plyr)
library(reshape2)
贝叶斯分类实现步骤:
- ##构建贝叶斯分类器
(1)#计算各类别出现的频率

(2)#计算各类别各特征属性频率

(3)#使用上述贝叶斯分类器对训练集进行训练,并测试

一个身高1.83米、体重59.0千克,脚长0.24米的人是男人还是女人呢?
- ##训练测试

训练集如下:
注:这里没有对身高、体重、脚长的特征属性值进行区间划分,也没有进行归一化或标准化处理,因为本次所使用的训练集仅有8个个体,进行区间分类的意义不大。虽然样本量少,但在本次预测中,预测的效率还是很高的。
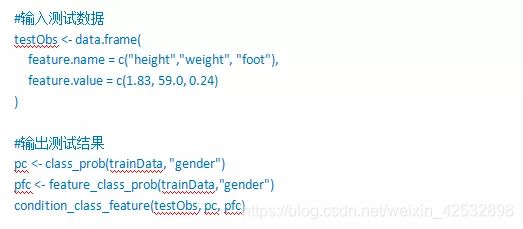
输出结果如下:

0代表女性,1代表男性,说明一个身高1.83米、体重59.0千克,脚长0.24米的人是女性的概率较大,可以判断为女性。
看到这,有人可能觉得只看数字自己也能判断出这个人是女性还是男性,这一点毫无疑问,多数人都能根据身高、体重、脚长判断一个人的性别。但上述例子中为了展示,仅测试了一个个体,如果有上万个甚至数亿个个体需要判断呢?利用模型统计的优势在于模型可以在很短的时间内实现对大型数据的计算和判断,并且根据大样本计算出的结果的准确性也会较高,而人工就不行啦。
注:若测试集是多条数据,则需要使用for循环对每一条测试数据调用一次condition_class_feature函数,并且需要对输入和输入的数据框进行转置和添加适当的辅助列。
限于篇幅,上述代码没有对每行添加注释,若需要获取带有注释的代码,[关注“数学算法的世界”,回复“贝叶斯分类”即可。]
数学算法的世界
数据分析|Python
R|SQL|Excel|科普