AI上推荐 之 逻辑回归模型与GBDT+LR(特征工程模型化的开端)
1. 前言
随着信息技术和互联网的发展, 我们已经步入了一个信息过载的时代,这个时代,无论是信息消费者还是信息生产者都遇到了很大的挑战:
- 信息消费者:如何从大量的信息中找到自己感兴趣的信息?
- 信息生产者:如何让自己生产的信息脱颖而出, 受到广大用户的关注?
为了解决这个矛盾, 推荐系统应时而生, 并飞速前进,在用户和信息之间架起了一道桥梁,一方面帮助用户发现对自己有价值的信息, 一方面让信息能够展现在对它感兴趣的用户前面。 推荐系统近几年有了深度学习的助推发展之势迅猛, 从前深度学习的传统推荐模型(协同过滤,矩阵分解,LR, FM, FFM, GBDT)到深度学习的浪潮之巅(DNN, Deep Crossing, DIN, DIEN, Wide&Deep, Deep&Cross, DeepFM, AFM, NFM, PNN, FNN, DRN), 现在正无时无刻不影响着大众的生活。
推荐系统通过分析用户的历史行为给用户的兴趣建模, 从而主动给用户推荐给能够满足他们兴趣和需求的信息, 能够真正的“懂你”。 想上网购物的时候, 推荐系统在帮我们挑选商品, 想看资讯的时候, 推荐系统为我们准备了感兴趣的新闻, 想学习充电的时候, 推荐系统为我们提供最合适的课程, 想消遣放松的时候, 推荐系统为我们奉上欲罢不能的短视频…, 所以当我们淹没在信息的海洋时, 推荐系统正在拨开一层层波浪, 为我们追寻多姿多彩的生活!
这段时间刚好开始学习推荐系统, 通过王喆老师的《深度学习推荐系统》已经梳理好了知识体系, 了解了当前推荐系统领域各种主流的模型架构和技术。 所以接下来的时间就开始对这棵大树开枝散叶,对每一块知识点进行学习总结。 所以接下来一块目睹推荐系统的风采吧!
这次整理重点放在推荐系统的模型方面, 先从传统推荐模型开始, 然后到深度学习模型。 传统模型的演化关系拿书上的一张图片, 便于梳理传统推荐模型的进化关系脉络, 对知识有个宏观的把握:

今天是推荐系统传统模型的第三篇, 迎来的是逻辑回归模型以及更加高级的GBDT+LR模型,前面介绍的协同过滤和矩阵分解同属于协同过滤家族, 之前分析过这协同过滤模型存在的劣势就是仅利用了用户与物品相互行为信息进行推荐, 忽视了用户自身特征, 物品自身特征以及上下文信息等,导致生成的结果往往会比较片面。 而今天的这两个模型是逻辑回归家族系列, 逻辑回归能够综合利用用户、物品和上下文等多种不同的特征, 生成较为全面的推荐结果。
相比于协同过滤和矩阵分解利用用户的物品“相似度”进行推荐, 逻辑回归模型将问题看成了一个分类问题, 通过预测正样本的概率对物品进行排序。这里的正样本可以是用户“点击”了某个商品或者“观看”了某个视频, 均是推荐系统希望用户产生“正反馈”行为, 因此逻辑回归模型将推荐问题转成成了一个点击率预估问题。 要注意这和前面的协同过滤不太一样了, 那里是“TOPN"推荐的问题, 而这里通过逻辑回归转成了一种点击率预估问题, 成了一种二分类, 如果模型预测用户会点击, 那么就进行推荐。 本篇文章会首先介绍逻辑回归模型,这个模型的重要性不言而喻, 现在凭借着易于并行, 模型简单, 训练开销小的优势依然在工程领域占有一席之地, 但是也正是因为这种简单, 直观使得它有了一定的局限性, 所以后面会分析逻辑回归模型的不足而引出更为强大的组合模型GBDT+LR, 这个模型利用GBDT的”自动化“特征组合, 使得模型具备了更高阶特征组合的能力,被称作特征工程模型化的开端, 所以这篇文章的重点在于这部分内容, 包括GBDT的原理, GBDT的在解决二分类问题上的细节和GBDT+LR模型的细节。 其实只要明白了GBDT和LR, 两者的组合就比较简单了, 所以本篇文章的重点放在了前者, 最后依然是基于GBDT+LR模型完成一个点击率预测的任务。
大纲如下:
- 逻辑回归模型
- GBDT模型的细节介绍
- GBDT+LR模型及及细节
- 编程实践
Ok, let’s go!
2. 逻辑回归模型
逻辑回归模型非常重要, 在推荐领域里面, 相比于传统的协同过滤, 逻辑回归模型能够综合利用用户、物品、上下文等多种不同的特征生成较为“全面”的推荐结果, 而在机器学习领域, 逻辑回归模型是面试当中非常容易被问到的一个算法, 因为表面上看似简单, 其实细节繁多, 在深度学习领域, 它又做为了神经网络中的最基础单一神经元, 成为了深度学习的基础性结构。所以掌握这个模型的一些重要细节是非常有必要的, 当然由于这里还是介绍推荐, 更多的细节在逻辑回归、优化算法和正则化的幕后细节补充这篇文章中, 这里只介绍比较重要的一些细节和在推荐中的应用。
逻辑回归是在线性回归的基础上加了一个 Sigmoid 函数(非线形)映射,使得逻辑回归称为了一个优秀的分类算法, 学习逻辑回归模型, 首先要记住一句话:逻辑回归假设数据服从伯努利分布,通过极大化似然函数的方法,运用梯度下降来求解参数,来达到将数据二分类的目的。 这是从我上面那篇文章中提炼出来的, 这里面涉及到了伯努利分布, 极大似然, 梯度下降, 二分类, sigmoid函数,损失函数的推导等, 具体内容看上面的链接吧,这里我们说回到推荐。
由于前面已经提到过, 逻辑回归模型已经将推荐问题转换成了一个点击率预测的问题, 而点击率预测就是一个典型的二分类, 正好适合逻辑回归进行处理, 那么逻辑回归是如何做推荐的呢? 过程如下:
- 将用户年龄、性别、物品属性、物品描述、当前时间、当前地点等特征转成数值型向量
- 确定逻辑回归的优化目标,比如把点击率预测转换成二分类问题, 这样就可以得到分类问题常用的损失作为目标, 训练模型
- 在预测的时候, 将特征向量输入模型产生预测, 得到用户“点击”物品的概率
- 利用点击概率对候选物品排序, 得到推荐列表
推断过程可以用下图来表示:
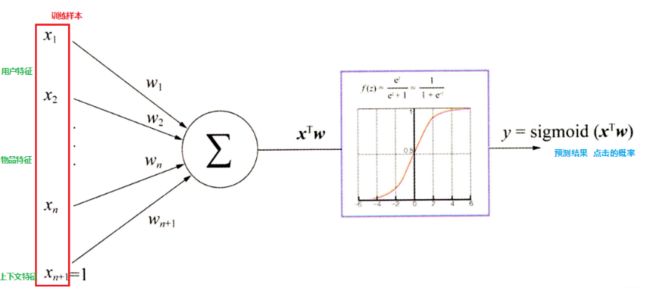
这里的关键就是每个特征的权重参数 w w w, 我们一般是使用梯度下降的方式, 首先会先随机初始化一批 w w w, 然后将特征向量(也就是我们上面数值化出来的特征)输入到模型, 就会通过计算会得到模型的预测概率, 然后通过对目标函数求导得到每个 w w w的梯度, 然后进行更新 w w w
这里的目标函数长下面这样:
J ( w ) = − 1 m ( ∑ i = 1 m ( y i log f w ( x i ) + ( 1 − y i ) log ( 1 − f w ( x i ) ) ) J(w)=-\frac{1}{m}\left(\sum_{i=1}^{m}\left(y^{i} \log f_{w}\left(x^{i}\right)+\left(1-y^{i}\right) \log \left(1-f_{w}\left(x^{i}\right)\right)\right)\right. J(w)=−m1(i=1∑m(yilogfw(xi)+(1−yi)log(1−fw(xi)))
求导之后的方式长这样:
w j ← w j − γ 1 m ∑ i = 1 m ( f w ( x i ) − y i ) x j i w_{j} \leftarrow w_{j}-\gamma \frac{1}{m} \sum_{i=1}^{m}\left(f_{w}\left(x^{i}\right)-y^{i}\right) x_{j}^{i} wj←wj−γm1i=1∑m(fw(xi)−yi)xji
这样通过若干次迭代, 就可以得到最终的 w w w了, 关于这些公式的推导,依然参考上面的那篇博客, 下面我们分析一下逻辑回归模型的优缺点。
优点:
- LR模型形式简单,可解释性好,从特征的权重可以看到不同的特征对最后结果的影响。
- 训练时便于并行化,在预测时只需要对特征进行线性加权,所以性能比较好,往往适合处理海量id类特征,用id类特征有一个很重要的好处,就是防止信息损失(相对于范化的 CTR 特征),对于头部资源会有更细致的描述
- 资源占用小,尤其是内存。因为只需要存储各个维度的特征值
- 方便输出结果调整。逻辑回归可以很方便的得到最后的分类结果,因为输出的是每个样本的概率分数,我们可以很容易的对这些概率分数进行cutoff,也就是划分阈值(大于某个阈值的是一类,小于某个阈值的是一类)
- 工程化需要, 在深度学习技术之前, 逻辑回归凭借易于并行化, 模型简单,训练开销小等特点,占领工程领域的主流, 因为即使工程团队发现了复杂模型会提升效果, 但一般如果没有把握击败逻辑回归的话仍然不敢尝试或者升级。
当然, 逻辑回归模型也有一定的局限性
- 表达能力不强, 无法进行特征交叉, 特征筛选等一系列“高级“操作(这些工作都得人工来干, 这样就需要一定的经验, 否则会走一些弯路), 因此可能造成信息的损失
- 准确率并不是很高。因为这毕竟是一个线性模型加了个sigmoid, 形式非常的简单(非常类似线性模型),很难去拟合数据的真实分布
- 处理非线性数据较麻烦。逻辑回归在不引入其他方法的情况下,只能处理线性可分的数据, 如果想处理非线性, 首先对连续特征的处理需要先进行离散化(离散化的目的是为了引入非线性),如上文所说,人工分桶的方式会引入多种问题。
- LR 需要进行人工特征组合,这就需要开发者有非常丰富的领域经验,才能不走弯路。这样的模型迁移起来比较困难,换一个领域又需要重新进行大量的特征工程。
所以如何自动发现有效的特征、特征组合,弥补人工经验不足,缩短LR特征实验周期,是亟需解决的问题, 也正是由于这些问题, 使得推荐系统继续朝着复杂化发展, 衍生出了因子分解机(FM), 组合模型等高维复杂模型, FM模型通过隐变量的方式,发现两两特征之间的组合关系,但这种特征组合仅限于两两特征之间, 这个模型后面也会介绍到。 深度学习时代之后, 多层神经网络凭借着其强大的表达能力替代了逻辑回归, 到现在, 基本上各大公司很少能看到逻辑回归的身影了。
3. GBDT模型
这个模型依然是一个非常重要的模型, 因为后面的GBDT+LR里面涉及到了这个模型, 而我发现大部分参考的文章里面直接拿原论文里面的图进行的描述, 略过了很多GBDT的细节,比如GBDT部分是如何进行二分类把样本放到叶子节点的?
GBDT全称梯度提升决策树,在传统机器学习算法里面是对真实分布拟合的最好的几种算法之一,在前几年深度学习还没有大行其道之前,gbdt在各种竞赛是大放异彩。原因大概有几个,一是效果确实挺不错。二是即可以用于分类也可以用于回归。三是可以筛选特征, 基于这几个原因使得这个模型依然是面试喜欢问的算法之一, 因此这个模型的细节我们也是有必要学习。
GBDT是通过采用加法模型(即基函数的线性组合),以及不断减小训练过程产生的误差来达到将数据分类或者回归的算法, 其训练过程如下:
gbdt通过多轮迭代, 每轮迭代会产生一个弱分类器, 每个分类器在上一轮分类器的残差基础上进行训练。 gbdt对弱分类器的要求一般是足够简单, 并且低方差高偏差。 因为训练的过程是通过降低偏差来不断提高最终分类器的精度。 由于上述高偏差和简单的要求,每个分类回归树的深度不会很深。最终的总分类器 是将每轮训练得到的弱分类器加权求和得到的(也就是加法模型)。
关于GBDT的详细细节, 在这篇文章中进行了详细的总结, 这里只想分析一下GBDT如何来进行二分类的,因为我们要明确一点就是gbdt 每轮的训练是在上一轮的训练的残差基础之上进行训练的, 而这里的残差指的就是当前模型的负梯度值, 这个就要求每轮迭代的时候,弱分类器的输出的结果相减是有意义的, 所以gbdt 无论用于分类还是回归一直都是使用的CART 回归树, 那么既然是回归树, 是如何进行二分类问题的呢? 如果是只用GBDT就可以进行二分类,那为啥后来又在GBDT的后面加上了逻辑回归模型呢? 如果是加上了逻辑回归模型, 那么两者究竟是怎么组合得到最后输出的呢? 后面两个问题的答案会在下一部分给出, 这里先分析一下GBDT的二分类问题, 也就是在二分类问题的时候, GBDT树的生成过程。
GBDT 来解决二分类问题和解决回归问题的本质是一样的,都是通过不断构建决策树的方式,使预测结果一步步的接近目标值, 但是二分类问题和回归问题的损失函数是不同的, 在上面那篇文章里面已经详细的整理了GBDT在回归问题上的树的生成过程, 损失函数和迭代原理, 回归问题中一般使用的是平方损失, 而二分类问题中, GBDT和逻辑回归一样, 使用的下面这个:
L = arg min [ ∑ i n − ( y i log ( p i ) + ( 1 − y i ) log ( 1 − p i ) ) ] L=\arg \min \left[\sum_{i}^{n}-\left(y_{i} \log \left(p_{i}\right)+\left(1-y_{i}\right) \log \left(1-p_{i}\right)\right)\right] L=argmin[i∑n−(yilog(pi)+(1−yi)log(1−pi))]
这个式子应该不用过多解释了, y i y_i yi是第 i i i个样本的观测值, 取值要么是0要么是1, 而 p i p_i pi是第 i i i个样本的预测值, 取值是0-1之间的概率(sigmoid了嘛),由于我们知道GBDT拟合的残差是当前模型的负梯度, 那么我们就需要求出这个模型的导数, 即 d L d p i \frac{dL}{dp_i} dpidL, 对于某个特定的样本, 求导的话就可以只考虑它本身, 去掉加和号, 那么就变成了 d l d p i \frac{dl}{dp_i} dpidl, 其中 l l l如下:
l = − y i log ( p i ) − ( 1 − y i ) log ( 1 − p i ) = − y i log ( p i ) − log ( 1 − p i ) − y i log ( 1 − p i ) = − y i ( log ( p i 1 − p i ) ) − log ( 1 − p i ) \begin{aligned} l &=-y_{i} \log \left(p_{i}\right)-\left(1-y_{i}\right) \log \left(1-p_{i}\right) \\ &=-y_{i} \log \left(p_{i}\right)-\log \left(1-p_{i}\right)-y_{i} \log \left(1-p_{i}\right) \\ &=-y_{i}\left(\log \left(\frac{p_{i}}{1-p_{i}}\right)\right)-\log \left(1-p_{i}\right) \end{aligned} l=−yilog(pi)−(1−yi)log(1−pi)=−yilog(pi)−log(1−pi)−yilog(1−pi)=−yi(log(1−pipi))−log(1−pi)
如果对逻辑回归非常熟悉的话, ( log ( p i 1 − p i ) ) \left(\log \left(\frac{p_{i}}{1-p_{i}}\right)\right) (log(1−pipi))一定不会陌生吧, 这就是对几率比取了个对数, 并且在逻辑回归里面这个式子会等于 θ X \theta X θX, 所以才推出了 p i = 1 1 + e − θ X p_i=\frac{1}{1+e^-{\theta X}} pi=1+e−θX1的那个形式。 这里令 η i = p i 1 − p i \eta_i=\frac{p_i}{1-p_i} ηi=1−pipi, 即 p i = η i 1 + η i p_i=\frac{\eta_i}{1+\eta_i} pi=1+ηiηi, 则上面这个式子变成了:
l = − y i log ( η i ) − log ( 1 − e log ( η i ) 1 + e log ( η i ) ) = − y i log ( η i ) − log ( 1 1 + e log ( η i ) ) = − y i log ( η i ) + log ( 1 + e log ( η i ) ) \begin{aligned} l &=-y_{i} \log \left(\eta_{i}\right)-\log \left(1-\frac{e^{\log \left(\eta_{i}\right)}}{1+e^{\log \left(\eta_{i}\right)}}\right) \\ &=-y_{i} \log \left(\eta_{i}\right)-\log \left(\frac{1}{1+e^{\log \left(\eta_{i}\right)}}\right) \\ &=-y_{i} \log \left(\eta_{i}\right)+\log \left(1+e^{\log \left(\eta_{i}\right)}\right) \end{aligned} l=−yilog(ηi)−log(1−1+elog(ηi)elog(ηi))=−yilog(ηi)−log(1+elog(ηi)1)=−yilog(ηi)+log(1+elog(ηi))
这时候, 我们对 l o g ( η i ) log(\eta_i) log(ηi)求导, 得
d l d log ( η i ) = − y i + e log ( η i ) 1 + e log ( η i ) = − y i + p i \frac{d l}{d \log (\eta_i)}=-y_{i}+\frac{e^{\log \left(\eta_{i}\right)}}{1+e^{\log \left(\eta_{i}\right)}}=-y_i+p_i dlog(ηi)dl=−yi+1+elog(ηi)elog(ηi)=−yi+pi
这样, 我们就得到了某个训练样本在当前模型的梯度值了, 那么残差就是 y i − p i y_i-p_i yi−pi。
下面我们来看GBDT的生成过程, 构建分类GBDT的步骤有两个:
-
初始化GBDT
和回归问题一样, 分类 GBDT 的初始状态也只有一个叶子节点,该节点为所有样本的初始预测值,如下:
F 0 ( x ) = arg min γ ∑ i = 1 n L ( y , γ ) F_{0}(x)=\arg \min _{\gamma} \sum_{i=1}^{n} L(y, \gamma) F0(x)=argγmini=1∑nL(y,γ)
上式里面, F F F代表GBDT模型, F 0 F_0 F0是模型的初识状态, 该式子的意思是找到一个 γ \gamma γ,使所有样本的 Loss 最小,在这里及下文中, γ \gamma γ都表示节点的输出,即叶子节点, 且它是一个 l o g ( η i ) log(\eta_i) log(ηi) 形式的值(回归值),在初始状态, γ = F 0 \gamma =F_0 γ=F0。
下面看例子(该例子来自下面的第二个链接), 假设我们有下面3条样本:
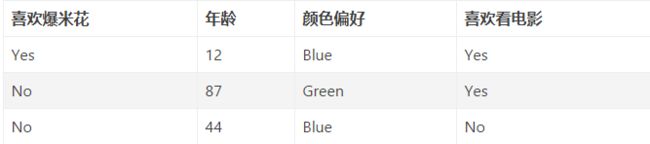
我们希望构建 GBDT 分类树,它能通过「喜欢爆米花」、「年龄」和「颜色偏好」这 3 个特征来预测某一个样本是否喜欢看电影,因为是只有 3 个样本的极简数据集,所以我们的决策树都是只有 1 个根节点、2 个叶子节点的树桩(Stump),但在实际应用中,决策树的叶子节点一般为 8-32 个。我们把数据代入上面的公式中求Loss:
Loss = L ( 1 , γ ) + L ( 1 , γ ) + L ( 0 , γ ) \operatorname{Loss}=L(1, \gamma)+L(1, \gamma)+L(0, \gamma) Loss=L(1,γ)+L(1,γ)+L(0,γ)
为了令其最小, 我们求导, 且让导数为0, 则:
Loss = L ( 1 , γ ) + L ( 1 , γ ) + L ( 0 , γ ) \operatorname{Loss}=L(1, \gamma)+L(1, \gamma)+L(0, \gamma) Loss=L(1,γ)+L(1,γ)+L(0,γ)
于是, 就得到了初始值 p = 2 3 = 0.67 , γ = l o g ( p 1 − p ) = 0.69 p=\frac{2}{3}=0.67, \gamma=log(\frac{p}{1-p})=0.69 p=32=0.67,γ=log(1−pp)=0.69, 模型的初识状态 F 0 ( x ) = 0.69 F_0(x)=0.69 F0(x)=0.69 -
循环生成决策树
这里回忆一下回归树的生成步骤, 其实有4小步, 第一就是计算负梯度值得到残差, 第二步是用回归树拟合残差, 第三步是计算叶子节点的输出值, 第四步是更新模型。 下面我们一一来看:-
计算负梯度得到残差
r i m = − [ ∂ L ( y i , F ( x i ) ) ∂ F ( x i ) ] F ( x ) = F m − 1 ( x ) r_{i m}=-\left[\frac{\partial L\left(y_{i}, F\left(x_{i}\right)\right)}{\partial F\left(x_{i}\right)}\right]_{F(x)=F_{m-1}(x)} rim=−[∂F(xi)∂L(yi,F(xi))]F(x)=Fm−1(x)
此处使用 m − 1 m-1 m−1棵树的模型, 计算每个样本的残差 r i m r_{im} rim, 就是上面的 y i − p i y_i-pi yi−pi, 于是例子中, 每个样本的残差:
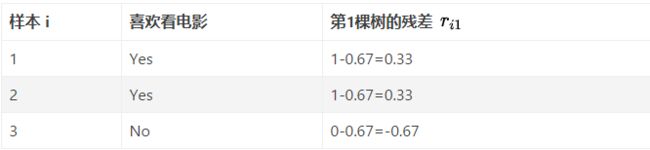
-
使用回归树来拟合 r i m r_{im} rim, 这里的 i i i表示样本哈,回归树的建立过程可以参考上面的链接文章,简单的说就是遍历每个特征, 每个特征下遍历每个取值, 计算分裂后两组数据的平方损失, 找到最小的那个划分节点。 假如我们产生的第2棵决策树如下:
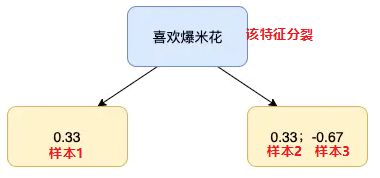
-
对于每个叶子节点 j j j, 计算最佳残差拟合值
γ j m = arg min γ ∑ x ∈ R i j L ( y i , F m − 1 ( x i ) + γ ) \gamma_{j m}=\arg \min _{\gamma} \sum_{x \in R_{i j}} L\left(y_{i}, F_{m-1}\left(x_{i}\right)+\gamma\right) γjm=argγminx∈Rij∑L(yi,Fm−1(xi)+γ)
意思是, 在刚构建的树 m m m中, 找到每个节点 j j j的输出 γ j m \gamma_{jm} γjm, 能使得该节点的loss最小。 那么我们看一下这个 γ \gamma γ的求解方式, 这里非常的巧妙。 首先, 我们把损失函数写出来, 对于左边的第一个样本, 有
L ( y 1 , F m − 1 ( x 1 ) + γ ) = − y 1 ( F m − 1 ( x 1 ) + γ ) + log ( 1 + e F m − 1 ( x 1 ) + γ ) L\left(y_{1}, F_{m-1}\left(x_{1}\right)+\gamma\right)=-y_{1}\left(F_{m-1}\left(x_{1}\right)+\gamma\right)+\log \left(1+e^{F_{m-1}\left(x_{1}\right)+\gamma}\right) L(y1,Fm−1(x1)+γ)=−y1(Fm−1(x1)+γ)+log(1+eFm−1(x1)+γ)
这个式子就是上面推导的 l l l, 因为我们要用回归树做分类, 所以这里把分类的预测概率转换成了对数几率回归的形式, 即 l o g ( η i ) log(\eta_i) log(ηi), 这个就是模型的回归输出值。而如果求这个损失的最小值, 我们要求导, 解出令损失最小的 γ \gamma γ。 但是上面这个式子求导会很麻烦, 所以这里介绍了一个技巧就是使用二阶泰勒公式来近似表示该式, 再求导, 还记得伟大的泰勒吗?
f ( x + Δ x ) ≈ f ( x ) + Δ x f ′ ( x ) + 1 2 Δ x 2 f ′ ′ ( x ) + O ( Δ x ) f(x+\Delta x) \approx f(x)+\Delta x f^{\prime}(x)+\frac{1}{2} \Delta x^{2} f^{\prime \prime}(x)+O(\Delta x) f(x+Δx)≈f(x)+Δxf′(x)+21Δx2f′′(x)+O(Δx)
这里就相当于把 L ( y 1 , F m − 1 ( x 1 ) ) L(y_1, F_{m-1}(x_1)) L(y1,Fm−1(x1))当做常量 f ( x ) f(x) f(x), γ \gamma γ作为变量 Δ x \Delta x Δx, 将 f ( x ) f(x) f(x)二阶展开:
L ( y 1 , F m − 1 ( x 1 ) + γ ) ≈ L ( y 1 , F m − 1 ( x 1 ) ) + L ′ ( y 1 , F m − 1 ( x 1 ) ) γ + 1 2 L ′ ′ ( y 1 , F m − 1 ( x 1 ) ) γ 2 L\left(y_{1}, F_{m-1}\left(x_{1}\right)+\gamma\right) \approx L\left(y_{1}, F_{m-1}\left(x_{1}\right)\right)+L^{\prime}\left(y_{1}, F_{m-1}\left(x_{1}\right)\right) \gamma+\frac{1}{2} L^{\prime \prime}\left(y_{1}, F_{m-1}\left(x_{1}\right)\right) \gamma^{2} L(y1,Fm−1(x1)+γ)≈L(y1,Fm−1(x1))+L′(y1,Fm−1(x1))γ+21L′′(y1,Fm−1(x1))γ2
这时候再求导就简单了
d L d γ = L ′ ( y 1 , F m − 1 ( x 1 ) ) + L ′ ′ ( y 1 , F m − 1 ( x 1 ) ) γ \frac{d L}{d \gamma}=L^{\prime}\left(y_{1}, F_{m-1}\left(x_{1}\right)\right)+L^{\prime \prime}\left(y_{1}, F_{m-1}\left(x_{1}\right)\right) \gamma dγdL=L′(y1,Fm−1(x1))+L′′(y1,Fm−1(x1))γ
Loss最小的时候, 上面的式子等于0, 就可以得到 γ \gamma γ:
γ 11 = − L ′ ( y 1 , F m − 1 ( x 1 ) ) L ′ ′ ( y 1 , F m − 1 ( x 1 ) ) \gamma_{11}=\frac{-L^{\prime}\left(y_{1}, F_{m-1}\left(x_{1}\right)\right)}{L^{\prime \prime}\left(y_{1}, F_{m-1}\left(x_{1}\right)\right)} γ11=L′′(y1,Fm−1(x1))−L′(y1,Fm−1(x1))
分子是残差, 而分母计算一下的话:
L ′ ′ ( y 1 , F ( x ) ) = d L ′ d log ( η 1 ) = d d log ( η 1 ) [ − y i + e log ( η 1 ) 1 + e log ( η 1 ) ] = d d log ( η 1 ) [ e log ( η 1 ) ( 1 + e log ( η 1 ) ) − 1 ] = e log ( η 1 ) ( 1 + e log ( η 1 ) ) − 1 − e 2 log ( η 1 ) ( 1 + e log ( η 1 ) ) − 2 = e log ( η 1 ) ( 1 + e log ( η 1 ) ) 2 = η 1 ( 1 + η 1 ) 1 ( 1 + η 1 ) = p 1 ( 1 − p 1 ) \begin{aligned} L^{\prime \prime}\left(y_{1}, F(x)\right) &=\frac{d L^{\prime}}{d \log (\eta_1)} \\ &=\frac{d}{d \log (\eta_1)}\left[-y_{i}+\frac{e^{\log (\eta_1)}}{1+e^{\log (\eta_1)}}\right] \\ &=\frac{d}{d \log (\eta_1)}\left[e^{\log (\eta_1)}\left(1+e^{\log (\eta_1)}\right)^{-1}\right] \\ &=e^{\log (\eta_1)}\left(1+e^{\log (\eta_1)}\right)^{-1}-e^{2 \log (\eta_1)}\left(1+e^{\log (\eta_1)}\right)^{-2} \\ &=\frac{e^{\log (\eta_1)}}{\left(1+e^{\log (\eta_1)}\right)^{2}} \\ &=\frac{\eta_1}{(1+\eta_1)}\frac{1}{(1+\eta_1)} \\ &=p_1(1-p_1) \end{aligned} L′′(y1,F(x))=dlog(η1)dL′=dlog(η1)d[−yi+1+elog(η1)elog(η1)]=dlog(η1)d[elog(η1)(1+elog(η1))−1]=elog(η1)(1+elog(η1))−1−e2log(η1)(1+elog(η1))−2=(1+elog(η1))2elog(η1)=(1+η1)η1(1+η1)1=p1(1−p1)
这时候, 就可以算出该节点的输出:
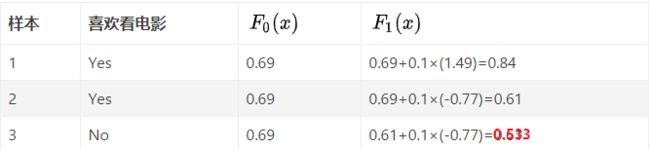
γ 11 = r 11 p 10 ( 1 − p 10 ) = 0.33 0.67 × 0.33 = 1.49 \gamma_{11}=\frac{r_{11}}{p_{10}\left(1-p_{10}\right)}=\frac{0.33}{0.67 \times 0.33}=1.49 γ11=p10(1−p10)r11=0.67×0.330.33=1.49
这里的下面 γ j m \gamma_{jm} γjm表示第 m m m棵树的第 j j j个叶子节点。 接下来是右边节点的输出, 包含样本2和样本3, 同样使用二阶泰勒公式展开:
L ( y 2 , F m − 1 ( x 2 ) + γ ) + L ( y 3 , F m − 1 ( x 3 ) + γ ) ≈ L ( y 2 , F m − 1 ( x 2 ) ) + L ′ ( y 2 , F m − 1 ( x 2 ) ) γ + 1 2 L ′ ′ ( y 2 , F m − 1 ( x 2 ) ) γ 2 + L ( y 3 , F m − 1 ( x 3 ) ) + L ′ ( y 3 , F m − 1 ( x 3 ) ) γ + 1 2 L ′ ′ ( y 3 , F m − 1 ( x 3 ) ) γ 2 \begin{array}{l} L\left(y_{2}, F_{m-1}\left(x_{2}\right)+\gamma\right)+L\left(y_{3}, F_{m-1}\left(x_{3}\right)+\gamma\right) \\ \approx L\left(y_{2}, F_{m-1}\left(x_{2}\right)\right)+L^{\prime}\left(y_{2}, F_{m-1}\left(x_{2}\right)\right) \gamma+\frac{1}{2} L^{\prime \prime}\left(y_{2}, F_{m-1}\left(x_{2}\right)\right) \gamma^{2} \\ +L\left(y_{3}, F_{m-1}\left(x_{3}\right)\right)+L^{\prime}\left(y_{3}, F_{m-1}\left(x_{3}\right)\right) \gamma+\frac{1}{2} L^{\prime \prime}\left(y_{3}, F_{m-1}\left(x_{3}\right)\right) \gamma^{2} \end{array} L(y2,Fm−1(x2)+γ)+L(y3,Fm−1(x3)+γ)≈L(y2,Fm−1(x2))+L′(y2,Fm−1(x2))γ+21L′′(y2,Fm−1(x2))γ2+L(y3,Fm−1(x3))+L′(y3,Fm−1(x3))γ+21L′′(y3,Fm−1(x3))γ2
求导, 令其结果为0,就会得到, 第1棵树的第2个叶子节点的输出:
γ 21 = − L ′ ( y 2 , F m − 1 ( x 2 ) ) − L ′ ( y 3 , F m − 1 ( x 3 ) ) L ′ ′ ( y 2 , F m − 1 ( x 2 ) ) + L ′ ′ ( y 3 , F m − 1 ( x 3 ) ) = r 21 + r 31 p 20 ( 1 − p 20 ) + p 30 ( 1 − p 30 ) = 0.33 − 0.67 0.67 × 0.33 + 0.67 × 0.33 = − 0.77 \begin{aligned} \gamma_{21} &=\frac{-L^{\prime}\left(y_{2}, F_{m-1}\left(x_{2}\right)\right)-L^{\prime}\left(y_{3}, F_{m-1}\left(x_{3}\right)\right)}{L^{\prime \prime}\left(y_{2}, F_{m-1}\left(x_{2}\right)\right)+L^{\prime \prime}\left(y_{3}, F_{m-1}\left(x_{3}\right)\right)} \\ &=\frac{r_{21}+r_{31}}{p_{20}\left(1-p_{20}\right)+p_{30}\left(1-p_{30}\right)} \\ &=\frac{0.33-0.67}{0.67 \times 0.33+0.67 \times 0.33} \\ &=-0.77 \end{aligned} γ21=L′′(y2,Fm−1(x2))+L′′(y3,Fm−1(x3))−L′(y2,Fm−1(x2))−L′(y3,Fm−1(x3))=p20(1−p20)+p30(1−p30)r21+r31=0.67×0.33+0.67×0.330.33−0.67=−0.77
可以看出, 对于任意叶子节点, 我们可以直接计算其输出值:
γ j m = ∑ i = 1 R i j r i m ∑ i = 1 R i j p i , m − 1 ( 1 − p i , m − 1 ) \gamma_{j m}=\frac{\sum_{i=1}^{R_{i j}} r_{i m}}{\sum_{i=1}^{R_{i j}} p_{i, m-1}\left(1-p_{i, m-1}\right)} γjm=∑i=1Rijpi,m−1(1−pi,m−1)∑i=1Rijrim -
更新模型 F m ( x ) F_m(x) Fm(x)
F m ( x ) = F m − 1 ( x ) + ν ∑ j = 1 J m γ m F_{m}(x)=F_{m-1}(x)+\nu \sum_{j=1}^{J_{m}} \gamma_{m} Fm(x)=Fm−1(x)+νj=1∑Jmγm
仔细观察该式,实际上它就是梯度下降——「加上残差」和「减去梯度」这两个操作是等价的,这里设学习率 ν \nu ν 为 0.1,则 3 个样本更新如下:
最终, 循环M次, 或者总残差低于预设的阈值时, 我们的分类GBDT的建模就完成了。
-
梳理一下GBDT二分类的这个思想,其实和逻辑回归的思想一样,逻辑回归是用一个线性模型去拟合 P ( y = 1 ∣ x ) P(y=1|x) P(y=1∣x)这个事件的对数几率 l o g p 1 − p = θ T x log\frac{p}{1-p}=\theta^Tx log1−pp=θTx, GBDT二分类也是如此, 用一系列的梯度提升树去拟合这个对数几率, 其分类模型可以表达为:
P ( Y = 1 ∣ x ) = 1 1 + e − F M ( x ) P(Y=1 \mid x)=\frac{1}{1+e^{-F_{M}(x)}} P(Y=1∣x)=1+e−FM(x)1
所以GBDT是可以进行二分类的,但是这里发现一个问题就是查GBDT和XGBOOST区别的时候, 总是会有一个传统的GBDT只用到了一阶导数, 而XGBOOST用到了二阶, 但是从上面的推导中发现GBDT不也用到了二阶导数? 对于这块, 我查了很多资料, 但是并没有找到一个满意的结果(资料太泛滥了, CSDN水文太多), 所以先把这个疑问在这里占个坑。
我们可以把树的生成过程理解成自动进行多维度的特征组合的过程,从根结点到叶子节点上的整个路径(多个特征值判断),才能最终决定一棵树的预测值, 另外,对于连续型特征的处理,GBDT 可以拆分出一个临界阈值,比如大于 0.027 走左子树,小于等于 0.027(或者 default 值)走右子树,这样很好的规避了人工离散化的问题。这样就非常轻松的解决了逻辑回归那里自动发现特征并进行有效组合的问题, 这也是GBDT的优势所在。
但是GBDT也会有一些局限性, 对于海量的 id 类特征,GBDT 由于树的深度和棵树限制(防止过拟合),不能有效的存储;另外海量特征在也会存在性能瓶颈,当 GBDT 的 one hot 特征大于 10 万维时,就必须做分布式的训练才能保证不爆内存。所以 GBDT 通常配合少量的反馈 CTR 特征来表达,这样虽然具有一定的范化能力,但是同时会有信息损失,对于头部资源不能有效的表达。
所以, 我们发现其实GBDT和LR的优缺点可以进行互补, 那么为啥不给它组合一下呢?
4. GBDT+LR模型及及细节
2014年, Facebook提出了一种利用GBDT自动进行特征筛选和组合, 进而生成新的离散特征向量, 再把该特征向量当做LR模型的输入, 来产生最后的预测结果, 这就是著名的GBDT+LR模型了。GBDT+LR 使用最广泛的场景是CTR点击率预估,即预测当给用户推送的广告会不会被用户点击。
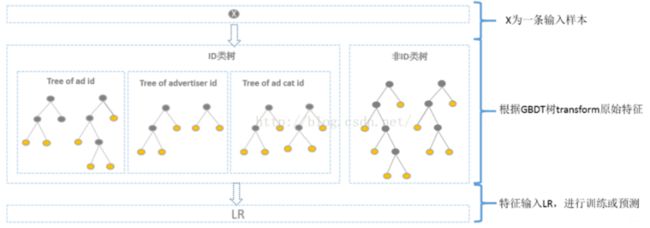
有了上面的铺垫, 这个模型解释起来就比较容易了, 模型的总体结构长下面这样:
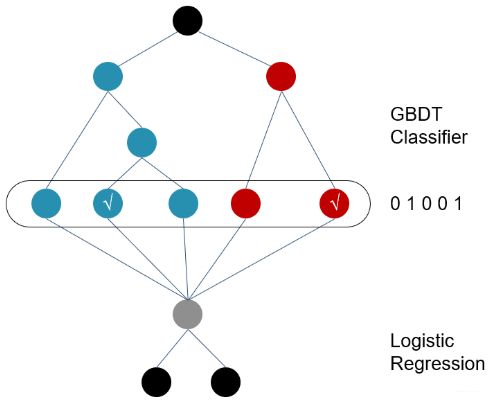
训练时,GBDT 建树的过程相当于自动进行的特征组合和离散化,然后从根结点到叶子节点的这条路径就可以看成是不同特征进行的特征组合,用叶子节点可以唯一的表示这条路径,并作为一个离散特征传入 LR 进行二次训练。
比如上图中, 有两棵树,x为一条输入样本,遍历两棵树后,x样本分别落到两颗树的叶子节点上,每个叶子节点对应LR一维特征,那么通过遍历树,就得到了该样本对应的所有LR特征。构造的新特征向量是取值0/1的。 比如左树有三个叶子节点,右树有两个叶子节点,最终的特征即为五维的向量。对于输入x,假设他落在左树第二个节点,编码[0,1,0],落在右树第二个节点则编码[0,1],所以整体的编码为[0,1,0,0,1],这类编码作为特征,输入到线性分类模型(LR or FM)中进行分类。
预测时,会先走 GBDT 的每棵树,得到某个叶子节点对应的一个离散特征(即一组特征组合),然后把该特征以 one-hot 形式传入 LR 进行线性加权预测。
这个方案应该比较简单了, 下面有几个关键的点我们需要了解:
- 通过GBDT进行特征组合之后得到的离散向量是和训练数据的原特征一块作为逻辑回归的输入, 而不仅仅全是这种离散特征
- 建树的时候用ensemble建树的原因就是一棵树的表达能力很弱,不足以表达多个有区分性的特征组合,多棵树的表达能力更强一些。GBDT每棵树都在学习前面棵树尚存的不足,迭代多少次就会生成多少棵树。
- RF也是多棵树,但从效果上有实践证明不如GBDT。且GBDT前面的树,特征分裂主要体现对多数样本有区分度的特征;后面的树,主要体现的是经过前N颗树,残差仍然较大的少数样本。优先选用在整体上有区分度的特征,再选用针对少数样本有区分度的特征,思路更加合理,这应该也是用GBDT的原因。
- 在CRT预估中, GBDT一般会建立两类树(非ID特征建一类, ID类特征建一类), AD,ID类特征在CTR预估中是非常重要的特征,直接将AD,ID作为feature进行建树不可行,故考虑为每个AD,ID建GBDT树。
- 树模型不能处理大量高维度离散数据的原因是容易导致过拟合, 但是具体是怎么导致的过拟合呢? 发现下面这张图片的理由说的非常好, 直接拿过来了。

5. 编程实践
关于GBDT, 暂且整理这么多, 下面我们就根据上面的模型架构进行一个简单的编程实践,下面链接里面的推荐系统遇上深度学习里面文文大佬已经给了一个例子, 这里我挑出一部分代码来进行解释一下, 这个模型其实比较简单, 这里就简单看一下过程, 最后面给出的github链接上会有一个kaggle比赛的数据集及详细的模型代码。
我们回顾一下上面的模型架构, 首先是要训练GBDT模型, GBDT的实现一般可以使用xgboost, 或者lightgbm。训练完了GBDT模型之后, 我们需要预测出每个样本落在了哪棵树上的哪个节点上, 然后通过one-hot就会得到一些新的离散特征, 这和原来的特征进行合并组成新的数据集, 然后作为逻辑回归的输入, 具体可以参考下面这个代码:
def gbdt_lr_predict(data, category_feature, continuous_feature): # 0.43616
# 离散特征one-hot编码
print('开始one-hot...')
for col in category_feature:
onehot_feats = pd.get_dummies(data[col], prefix = col)
data.drop([col], axis = 1, inplace = True)
data = pd.concat([data, onehot_feats], axis = 1)
print('one-hot结束')
train = data[data['Label'] != -1]
target = train.pop('Label')
test = data[data['Label'] == -1]
test.drop(['Label'], axis = 1, inplace = True)
# 划分数据集
print('划分数据集...')
x_train, x_val, y_train, y_val = train_test_split(train, target, test_size = 0.2, random_state = 2018)
print('开始训练gbdt..')
gbm = lgb.LGBMRegressor(objective='binary',
subsample= 0.8,
min_child_weight= 0.5,
colsample_bytree= 0.7,
num_leaves=100,
max_depth = 12,
learning_rate=0.05,
n_estimators=10,
)
gbm.fit(x_train, y_train,
eval_set = [(x_train, y_train), (x_val, y_val)],
eval_names = ['train', 'val'],
eval_metric = 'binary_logloss',
# early_stopping_rounds = 100,
)
model = gbm.booster_
print('训练得到叶子数')
gbdt_feats_train = model.predict(train, pred_leaf = True)
gbdt_feats_test = model.predict(test, pred_leaf = True)
gbdt_feats_name = ['gbdt_leaf_' + str(i) for i in range(gbdt_feats_train.shape[1])]
df_train_gbdt_feats = pd.DataFrame(gbdt_feats_train, columns = gbdt_feats_name)
df_test_gbdt_feats = pd.DataFrame(gbdt_feats_test, columns = gbdt_feats_name)
print('构造新的数据集...')
train = pd.concat([train, df_train_gbdt_feats], axis = 1)
test = pd.concat([test, df_test_gbdt_feats], axis = 1)
train_len = train.shape[0]
data = pd.concat([train, test])
del train
del test
gc.collect()
# # 连续特征归一化
# print('开始归一化...')
# scaler = MinMaxScaler()
# for col in continuous_feature:
# data[col] = scaler.fit_transform(data[col].values.reshape(-1, 1))
# print('归一化结束')
# 叶子数one-hot
print('开始one-hot...')
for col in gbdt_feats_name:
print('this is feature:', col)
onehot_feats = pd.get_dummies(data[col], prefix = col)
data.drop([col], axis = 1, inplace = True)
data = pd.concat([data, onehot_feats], axis = 1)
print('one-hot结束')
train = data[: train_len]
test = data[train_len:]
del data
gc.collect()
x_train, x_val, y_train, y_val = train_test_split(train, target, test_size = 0.3, random_state = 2018)
# lr
print('开始训练lr..')
lr = LogisticRegression()
lr.fit(x_train, y_train)
tr_logloss = log_loss(y_train, lr.predict_proba(x_train)[:, 1])
print('tr-logloss: ', tr_logloss)
val_logloss = log_loss(y_val, lr.predict_proba(x_val)[:, 1])
print('val-logloss: ', val_logloss)
print('开始预测...')
y_pred = lr.predict_proba(test)[:, 1]
print('写入结果...')
res = pd.read_csv('data/test.csv')
submission = pd.DataFrame({
'Id': res['Id'], 'Label': y_pred})
submission.to_csv('submission/submission_gbdt+lr_trlogloss_%s_vallogloss_%s.csv' % (tr_logloss, val_logloss), index = False)
print('结束')
6. 总结
这篇文章用了三天的时间, 主要的不是GBDT+LR模型本身复杂, 这个模型相反用了很少的篇幅就可以把原理说明白, 但是LR和GBDT本身才是更重要的, 所以这三天里我重点又看了一下逻辑回归的细节和GBDT的细节, 之前没有详细的了解GBDT, 而这次也借着这个机会看了一下, 有很多收获, 当然花时间也比较多, 关于LR和逻辑回归的细节, 我单独整理了两篇博客, 具体可以参考下面放出的链接。 所以这篇文章相对来说就不是太长了, 有了前面的铺垫, 整理起来也比较容易。 下面简单的回顾一下:
首先今天的这篇文章属于逻辑回归的家族系列了, 它能够在原来协同过滤的基础上利用更多的特征, 比如用户特征,物品特征和上下文特征, 并且也增强了模型的可解释性。一上来是解释了一下逻辑回归的原理, 逻辑回归比较简单, 它把推荐问题转换成了一个CTR预测的二分类问题, 并根据输入样本构造的各种特征进行分类, 但是它需要人为的进行特征工程, 于是人的经验在里面决定了模型效果的很大一部分, 且这个模型不太适合于非线性样本。 然后介绍了GBDT的原理, 重点是GBDT如何进行二分类的, 这个我参考了很多资料, 毕竟GBDT里面都是回归树, 原来是在拟合一个对数几率, 这个也是这次我新学到的一些知识。 GBDT模型可以进行特征的自由组合和筛选, 但是对于处理高维系数特征能力不强, 所以Facebook就把它俩进行了组合, 先有GBDT进行特征的筛选和组合,生成一些离散的向量, 然后作为了逻辑回归的输入,最后逻辑回归进行最后的预测, 这种方式比前面那两个哥们单独的表现要好。 这个模型也实现了特征工程模型化的开端, 为后面的DL打下了基础。 当然, 这个模型也不是没有缺点的, GBDT本身非常容易过拟合, 且在特征转换上丢了大量特征的信息, 所以这个模型参数调起来感觉也是挺麻烦的。
最后, 就是通过编程实现了一下这个模型, 当然这里只展示了一下外貌, 这个是2014年kaggle上的一个ctr预测的题目, 详细的可以看下面的GitHub链接, 那里面有详细的代码, LR, GBDT和两者组合对比了一下, 确实这个效果要好, 但需要调参。
好了, 机器学习模型目前整理了是三个了, 上面图里面还有最后一块FM与FFM家族, 再加上这个, 上面图里的模型基本全了, 当然可能这些模型在如今推荐领域都基本用不上了, 但是里面的一些思想或许在后面与深度学习碰撞一些火花。
由于最近事情有些多, 后面计划一周更新一篇推荐系列,毕竟不能占用太多的正常学习时间, 下周计划整理完FM与FFM家族, 后面就进入深度学习的浪潮之巅 Rush
参考:
- 王喆 - 《深度学习推荐系统》
- 决策树之 GBDT 算法 - 分类部分
- 深入理解GBDT二分类算法
- 逻辑回归、优化算法和正则化的幕后细节补充
- 梯度提升树GBDT的理论学习与细节补充
- 推荐系统遇上深度学习(十)–GBDT+LR融合方案实战
- CTR预估中GBDT与LR融合方案
- GBDT+LR算法解析及Python实现
- 常见计算广告点击率预估算法总结
- 腾讯大数据:CTR预估中GBDT与LR融合方案
- https://github.com/neal668/LightGBM-GBDT-LR/blob/master/GBFT%2BLR_simple.py
- GBDT原理及利用GBDT构造新的特征-Python实现
- Kaggle : Display Advertising Challenge( ctr 预估 )
- 逻辑回归的常见面试点总结
- GBDT–分类篇
论文
- http://quinonero.net/Publications/predicting-clicks-facebook.pdf 原论文
- Predicting Clicks: Estimating the Click-Through Rate for New Ads\
- Greedy Fun tion Approximation : A Gradient Boosting
整理这篇文章的同时, 也刚建立了一个GitHub项目, 准备后面把各种主流的推荐模型复现一遍,并用通俗易懂的语言进行注释和逻辑整理, 今天的GBDT+LR模型已经上传, 这次是用的kaggle比赛的一个ctr数据集,感兴趣的可以看一下
筋斗云:https://github.com/zhongqiangwu960812/AI-RecommenderSystem