模式类实验数据的生成
模式类实验数据的生成
摘要: 本次实验的主要目的是学习模式类实验数据的生成。本次实验第一部分通过调用自己编写的varlist函数,输入不同参数,可以产生自定义数量的一维,二维,三维随机点,绘制出对应的散点图。第二部分绘制了随机数的直方图,随机矢量二维散点图和三维散点图以及三组二维投影散点图。第三部分利用meshgrid函数生成一个二维网格,利用mvnpdf函数计算在每个网格点上的概率密度函数值,并绘制出这些函数值的三维曲面图。
一、技术论述
在matlab中提供了很多产生随机数和随机向量的函数,以及计算随机函数的概率密度值的函数。下面是几个常用的函数:
1.rand():生成均匀分布随机数
2.randn():生成高斯分布随机数
3.mvnrnd():生成多元高斯分布的随机向量矩阵
4.mvnpdf():计算多元高斯分布的概率密度函数值
5.reshape():重新调整矩阵的行数、列数、维数
6.mesh():生成由X,Y,Z定义的网线图
7.meshgrid():从数组a和b产生网格
8.hist():绘制对应数据的直方图
9.plot():绘制对应数据的二维散点图
10.plot3():绘制对应数据的三维散点图
11.bar():绘制对应数据的直方图
在本次实验的第二部分,要求绘制三维随机矢量数据集合的二维投影散点图,即指定模式向量的其中两个分量,将集合中每个向量的这两个分量提取出来构成一个二维模式子分量的向量集合,然后在二维平面上画出该子集分量集合的二维散点图,具体做法是:用plot函数,只取所需要的维度来绘制二维散点图。
二、实验结果
1、利用rand()函数生成均匀分布的随机数
1.1、调用自定义函数varlist(1,1000,10,70),在一维区间[10,70],生成1000个均匀分布的随机数,并统计并绘制这些数的直方图,具体实验结果图1.1所示:

图1.1 1000个rand函数的随机数直方图
1.2、调用自定义函数varlist(2,5000,1,5,20,30),在二维区间[1,5]*[20,30]中,生成5000个均匀分布的二维随机点,并绘制它们的二维散点图,具体实验结果图1.2所示:
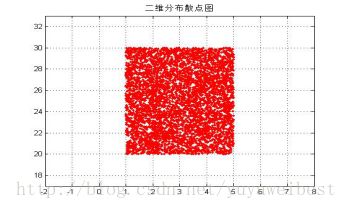
图1.2 5000个rand函数产生的二维散点图
1.3、调用自定义函数varlist(3,10000,10,50,30,60,10,15),在三维区间[10,50]-[30,60]*[10,15]中,生成10000个均匀分布的三维随机点,并绘制它们的三维散点图,具体实验结果图1.3所示:
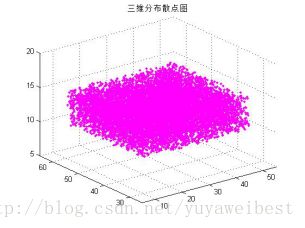
图1.3 10000个三维随机数的散点图
2、 生成高斯分布的随机数与随机向量矩阵
2.1、调用自定义函数self_randn(10000,1,5,2,15),生成两组1000均值分别为1,2,方差为5,15的一维高斯分布的随机数,绘制这些点的直方图,实验结果见图2.1.1和图2.1.2:
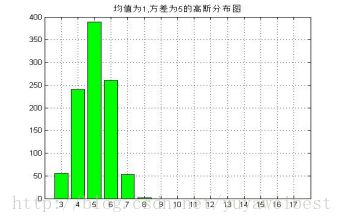
图2.1.1 均值为1,方差5的高斯分布图
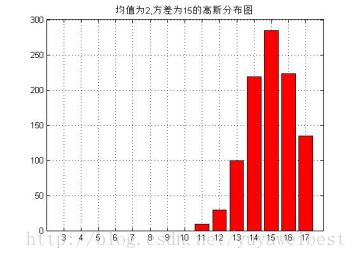
图2.1.2 均值为2,方差15的高斯分布图
2.2、生成三组各1000个具有不同均值矢量和协方差矩阵的二维随机矢量,并绘制出它们的二维散点图,其中品红色的的期望向量为:[1,3],方差矩阵为:[4 0;0 3],蓝色的期望向量为:[13,13],方差矩阵为:[6 0;0 8],黑色的期望向量:[25,23],方差矩阵:[2 0;0 4],具体实验结果图2.2所示:
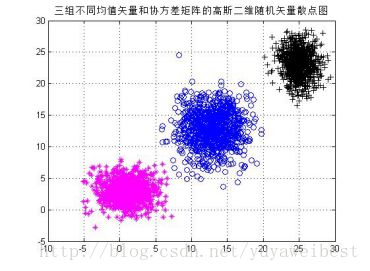
图2.2 三组高斯二维随机矢量散点图
2.3、生成五组各1000个具有不同均值矢量和协方差矩阵的三维随机矢量,并绘制出它们的三维散点图,其中黑色的的期望向量为:[-12 13 -4],方差矩阵为:[2 0 0;0 3 0;0 0 4],红色的期望向量为:[-8 10 3],方差矩阵为:[1 0 0;0 2 0;0 0 3],品红色的期望向量:[3,8,3],方差矩阵:[0 0 0;0 2 0;0 0 3],灰色的期望向量:[-7,0,4],方差矩阵:[1 0 0;0 3 0;0 0 3],绿色的期望向量:[7,0,-4],方差矩阵:[1 0 0;0 3 0;0 0 2],具体实验结果见图2.3所示:

图2.3 五组高斯三维随机矢量散点图
2.4、取上述三维矢量数据的第二、三维,第一、三维和第一、二维,分别绘制出二维投影散点图, 实验结果具体见图2.4.1、2.4.2和2.4.3。

图2.4.1 第2、3维散点图

图2.4.2 第1、3维散点图
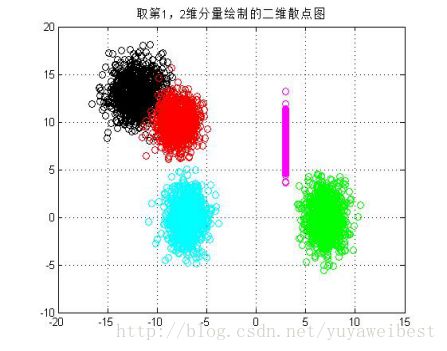
图2.4.3 第1、2维散点图
3、 利用mvnpdf函数计算概率密度函数值并绘制三维曲面图
首先,确定一个二维的均值矢量[2 2]和协方差矩阵[1 0;0 1],然后,利用MATLAB中的meshgrid函数生成一个二维网格,利用mvnpdf函数计算每一个网格点上的概率密度函数值,绘制这些函数值的三维曲面图,实验结果见图3:

图3 风格点上概率密度函数值的三维曲面图
三、实验结果讨论
使用公式(m-n)*rand()+n产生n-m之间均匀分布的随机数,通过观察实验结果图1.1的1000个样本,可以发现产生的数大致均匀分布,观察图1.2和1.3,可以看出,生成的随机数在二维、三维空间也大致均匀分布。图2.1.1和图2.1.2,可以看出,改变均值和方差可以影响高斯型随机的分布。图2.2,图2.3,均值MU决定了随机数组的中心点位置,而协方差矩阵决定了随机点在中心点附近的分布。图2.4.1,图2.4.2和图2.4.3,分别是三维随机矢量数据集合的二维投影散点图。图2.5是概率密度的三维曲面图,从图像的颜色差异可以看出函数值大小的差异,函数值由环状内部向外逐渐减小。
由以上实验及其结果可以发现, MATLAB中有自带的生成随机数和随机向量的函数,可以产生模式类的数据,可以在不同的区间生成不同维数的数据,产生的数据具有随机性。在高斯分布的随机数中,不同的均值矢量或不同的协方差矩阵产生的数据是不一样的。
附录:matlab代码
%============第一问==============
varlist(1,1000,10,70);
varlist(2,5000,1,5,20,30);
varlist(3,10000,10,50,30,60,10,15);
%函数输入参数可变,由输入参数决定产生随机数种类,画出对应的散点图
%格式:维数+随机个数+范围上限+下限
%如三维[10,50]*[30,60]*[10,15]生成10000个随机点,表示:%varlist(3,10000,10,50,30,60,10,15)
function varlist(varargin)
if(nargin==4)%一维,如varlist(1,1000,10,70)
for j=1:varargin{2}%varargin{2}代表第二个参量:随机点个数
y1(j)=rand()*(varargin{4}-varargin{3})+varargin{3};
end
b=hist(y1,varargin{3}:varargin{4});
figure (1)
bar(varargin{3}:varargin{4},b,'g');
title('一维分布直方图');
grid on
elseif ( nargin==6)
%绘制出它们的二维散点图,如varlist(2,5000,1,5,20,30)
for j=1:varargin{2}
y2(j,1)=rand()*(varargin{4}-varargin{3})+varargin{3};
y2(j,2)=rand()*(varargin{6}-varargin{5})+varargin{5};
end
figure (2)
plot(y2(:,1),y2(:,varargin{1}),'r.');
xlim([varargin{3}-3,varargin{4}+3]);%设置X坐标范围
ylim([varargin{5}-3,varargin{6}+3]);%设置Y坐标范围
title('二维分布散点图');
grid on
elseif( nargin==8)
%绘制出它们的三维散点图,如varlist(3,10000,10,50,30,60,10,15)
for i=1:varargin{2}
y3(i,1)=rand()*(varargin{4}-varargin{3})+varargin{3};
y3(i,2)=rand()*(varargin{6}-varargin{5})+varargin{5};
y3(i,3)=rand()*(varargin{8}-varargin{7})+varargin{7};
end
figure (3)
scatter3(y3(:,1),y3(:,2),y3(:,3),'m.');
xlim([[varargin{3}-5,varargin{4}+5]]);%设置X坐标范围
ylim([[varargin{5}-5,varargin{6}+5]]);%设置Y坐标范围
zlim([[varargin{7}-5,varargin{8}+5]]);%设置Z坐标范围
title('三维分布散点图');
grid on
else disp('只能输入参数个数为4,6,8');
%输入参数不是4,6,8时,提示错误
end
%============第二问==============
self_randn(1000,1,5,2,15);
%函数输入参数个数固定为5,否则输出出错,输入为两组数据的直方图
%格式:随机个数+均值+方差+均值+方差
%两组1000个均值分别为1,2,方差5,15随机数,画直方图
%表示:self_randn(1000,1,5,2,15)
function self_randn(varargin)
if(nargin==5)
for j=1:varargin{1}
y(j,1)=randn()*sqrt(varargin{2})+varargin{3};
y(j,2)=randn()*sqrt(varargin{4})+varargin{5};
end
G1=hist(y(:,1),varargin{3}-2:varargin{5}+2);
G2=hist(y(:,2),varargin{3}-2:varargin{5}+2);
figure (1)
bar(varargin{3}-2:varargin{5}+2,G1,'g');
title(['均值为',num2str(varargin{2}),',方差为',num2str(varargin{3}),'的高斯分布图']);
grid on
figure (2)
bar(varargin{3}-2:varargin{5}+2,G2,'r');
title(['均值为',num2str(varargin{4}),',方差为',num2str(varargin{5}),'的高斯分布图']);
grid on
else disp('只能输入参数个数为5');
end
%绘制三组各1000个不同均值矢量和协方差矩阵的二维随机矢量
%并绘制散点图
%mvnrnd(MU,SIGMA,cases)
%产生二维正态随机数,MU为期望向量,SIGMA为协方差矩阵,cases为规模
MU1=[1,3];
MU2=[13,13];
MU3=[25,23];
SIGMA1=[4 0;0 3];
SIGMA2=[6 0;0 8];
SIGMA3=[2 0;0 4];
h1=mvnrnd(MU1,SIGMA1,1000);
h2=mvnrnd(MU2,SIGMA2,1000);
h3=mvnrnd(MU3,SIGMA3,1000);
figure(1)
plot(h1(:,1),h1(:,2),'m*',h2(:,1),h2(:,2),'bo',h3(:,1),h3(:,2),'k+');
title('三组不同均值矢量和协方差矩阵的高斯二维随机矢量散点图');
grid on
%绘制五组高斯三维随机矢量散点图
%mvnrnd(MU,SIGMA,cases)
%MU为期望向量,SIGMA为协方差矩阵,cases为规模
MU1=[-12 13 -4];
MU2=[-8 10 3];
MU3=[3,8,3];
MU4=[-7,0,4];
MU5=[7,0,-4];
SIGMA1=[2 0 0;0 3 0;0 0 4];
SIGMA2=[1 0 0;0 2 0;0 0 3];
SIGMA3=[0 0 0;0 2 0;0 0 3];
SIGMA4=[1 0 0;0 3 0;0 0 3];
SIGMA5=[1 0 0;0 3 0;0 0 2];
h1=mvnrnd(MU1,SIGMA1,1000);
h2=mvnrnd(MU2,SIGMA2,1000);
h3=mvnrnd(MU3,SIGMA3,1000);
h4=mvnrnd(MU4,SIGMA4,1000);
h5=mvnrnd(MU5,SIGMA5,1000);
figure(1)
plot3(h1(:,1),h1(:,2),h1(:,3),'ko',h2(:,1),h2(:,2),h2(:,3),'ro',h3(:,1),h3(:,2),h3(:,3),'mo',h4(:,1),h4(:,2),h4(:,3),'co',h5(:,1),h5(:,2),h5(:,3),'go');
title('五组不同均值矢量和协方差矩阵的三维散点图');
grid on
%绘制三维随机矢量的二维散点图
figure(2)
plot(h1(:,2),h1(:,3),'ko',h2(:,2),h2(:,3),'ro',h3(:,2),h3(:,3),'mo',h4(:,2),h4(:,3),'co',h5(:,2),h5(:,3),'go');
title('取第2,3维分量绘制的二维散点图');
grid on
figure(3)
plot(h1(:,1),h1(:,3),'ko',h2(:,1),h2(:,3),'ro',h3(:,1),h3(:,3),'mo',h4(:,1),h4(:,3),'co',h5(:,1),h5(:,3),'go');
title('取第1,3维分量绘制的二维散点图');
grid on
figure(4)
plot(h1(:,1),h1(:,2),'ko',h2(:,1),h2(:,2),'ro',h3(:,1),h3(:,2),'mo',h4(:,1),h4(:,2),'co',h5(:,1),h5(:,2),'go')
title('取第1,2维分量绘制的二维散点图');
grid on
%============第三问==============
%用函数meshgrid和mvnpdf画图
MU=[2,2];%二维的均值矢量
SIGMA=[1 0;0 1];
[M,N]=meshgrid(-5:0.1:9,-5:0.1:9);
X=mvnpdf([M(:),N(:)],MU,SIGMA);
Y=reshape(X,size(M));
mesh(M,N,Y);
title ('网格点上概率密度函数值的三维曲面图');
grid on