【Leetcode】数论刷题解析（持续更新）

本人使用环境Python3+Pycharm。最近恢复刷题，持续更新，能点赞的点点赞，抱拳了。想要啥题号自己搜一下没有去我别的文章中搜，我目前的规划就是先刷数论，边刷编写哈~（我是刷完了但是写文章花时间呀，不要喷我噻）
目前涉及的题目编号：8，172，191，231，258，268，292，326，342
找题就复制这个，亲测好用：【你要查找的题号】
【8】字符串转换整数 (atoi)
题目分析：这个题就是要做以下几件事，把字符串空格去掉，然后把剩下的变成数字。其中您要考虑计算机存储数字的最大值与最小值，以及是否是-号开头。搞明白以上几件事我们就可以去写这个代码了。

import re
class Solution:
    def myAtoi(self, str: str) -> int:
        return max(min(int(*re.findall('^[\+\-]?\d+', str.lstrip())), 2 ** 31 - 1), -2 ** 31)

    def myAtoi2(self, str: str) -> int:
        return max(min(int(*re.findall('^[\+\-]?\d+', str.lstrip())), (1 << 31) - 1), -1 << 31)

正则，lstrip（），int()类型转换，max（）min（）这里都不赘述
这里说一下*re是个什么鬼？
我们来看一下没有*什么后果

class Solution:
    def myAtoi3(self, str: str) -> int:
        return int(*re.findall('^[\+\-]?\d+', str.lstrip()))

    def myAtoi4(self, str: str) -> int:
        return int(re.findall('^[\+\-]?\d+', str.lstrip()))
s = Solution()
print(s.myAtoi3("2147483646"))
print(s.myAtoi4("2147483646"))

运行结果是：

这地方写的也非常明确就是在python中int()转换里面必须是string类型，类字节对象或者是数字，而不能是list。我们再来看这个源码：

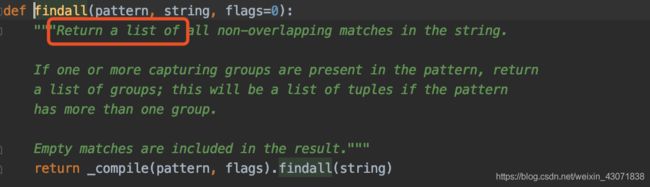
清晰可见这个地方返回的是一个list，所以上面那个转换是有问题的，那么问题来了*re.lstrip()返回的是个什么？看下面拆包解析：

到此该说的都说完了，剩下我再记一个东西，因为我用的python，我之前也是写java的但是python吧对于这道题木有像Java那种MAX_INTEGER，而且python3和python2是不一样的，这就导致我语法老师记错。看下python3中的最大整数

import sys
print(sys.getsizeof(sys.maxsize))
print(sys.maxsize)

反正就是这两个方法，第一个是看这个数占了多少个字节，第二个是看python的最大int值,我在mac测的是占了64位也就是2^63 -1。

【172】阶乘后的零
题目要求：给定一个整数 n，返回 n! 结果尾数中零的数量。时间复杂度不超过logn
题目分析：硬核解法就是直接把n！算出来，然后数0。确实能够实现，但是时间复杂度是O(n)。接下来我们就要转变思想，怎么搞这个东西，首先既然是数0，那么什么会产生0？一定是2x5，4x5，6x5，8x5,或者是10，20这些，他们都有一个共同的特点就是他们都可以拆成5和……，2和……。
到这里我们会发现2的个数永远比5多10个数 我们就可以发现5只有2个，2可以有5个，这个地方一定要理解。这道题已经让我们从n！的结果数0，变成了数阶乘中2和5的最小个数，再变成数5的个数。说到这里这个问题就很明了了。
O(n)=log5(n)

class Solution127:
    def trailingZeroes(self, n: int) -> int:
    	#sum 是为了计算5的个数
        sum = 0
        while n >= 5:
        #//是整数除法，比如25里面有5个5，10里面有2个5
            n = n // 5
            sum += n
        return sum

【191】位1的个数
题目要求：编写一个函数，输入是一个无符号整数，返回其二进制表达式中数字位数为 ‘1’ 的个数（也被称为汉明重量）
题目分析：如字面意思这个真的特别简单，首先哈这是一个无符号整数Python3中可以用bin()直接把数字变成2进制，然后问我们把这个2进制变成字符串，最后数里面的1就好了，代码如下：

    def hammingWeight(self, n: int) -> int:
        return bin(n).count('1')

再就是又涉及到位运算，如果是奇数的话最右边一位一定是1，所以n&(n-1)最右边的1位就会变成0。如果是偶数的话最右边一位是0，n&(n-1)一定会向从右向左遇到的第一个1进行借位，在进行与运算的时候只会涉及从右向左数遇到的第一个1，至于其他的1都不会被影响，所以还是会影响最右边的1然后把它变成0，因为从最右边的1借位，从该位向右都会由0变成1，然后做与运算，代码如下：

    def hammingWeight(self, n: int) -> int:
        count = 0
        while n > 0:
            n &= (n - 1)
            count += 1
        return count

【231】2的幂
题目要求：给定一个整数，编写一个函数来判断它是否是 2 的幂次方
题目分析：这个大白话，我觉得大家都看的懂。怎么搞呢？最简单的就是一遍遍模看余数，就像这样：

    def isPowerOfTwo(self, n: int) -> bool:
        tag = 1
        if (n < 0):
            return False
        while (n >= tag):
            if (n == tag):
                return True
            else:
                tag *= 2
        return False

这个代码不解释了，要是看不懂em……木得办法了。接下来说一下如何优化这个东西，这就又要涉及到位运算了，这里说个结论：一个数是不是2的幂次方就看这个数 与运算 这个数减1 是不是0。 这个结论怎么得出来的呢，其实很好想，与运算1&0是0，1&1是1。我们设想4 它的2进制是0100，3的二进制是0011，5的二进制是0101。那么现在来看从5到4一定是少了最末位的1，因为2^0是1，所以无论增减2进制都是要在最后一位进行操作。我们来看一下这个命令 1<<31 左移31位，每左移一次就是乘2，想一下是不是从1→10→100→1000……而他们减1 是不是0 →01→011→0111……。所以这个问题就很明了了，知道这个这个代码就变成了：

    def isPowerOfTwo_3(self, n: int) -> bool:
        if (n <= 0):
            return False
        return n & (n - 1) == 0

再来说另外一种我看到的，**还是先说结论：这个数y是2的幂次方，那么y&(-y)一定是y。**为啥咧？这就涉及到补码的问题，大家可以自己百度，整体的思路就跟上面我说的与运算差不多。代码如下：

    def isPowerOfTwo_2(self, n: int) -> bool:
        if (n <= 0):
            return False
        return n & (-n) == n

理解归理解，还是背结论比较好，你也不能天天纠结1+1为什么等于2，但是能理解是最好的。
【258】各位相加
题目要求：给定一个非负整数 num，反复将各个位上的数字相加，直到结果为一位数。
题目解析：看到这个题我第一反应是想怎么把这个数字拆成一位一位的，之前记得有个方法但是突然想不起来了，我就干脆不想了就把这个数字变成string然后再利用map拆成数组，然后一位位加起来就好了，代码如下：

    def addDigits(self, num: int) -> int:
        while num >= 10:
            digit = list(map(int, str(num)))
            #因为我不想再用一个变量接结果我就把num先置零，以防历史值影响计算
            num = 0
            for i in range(len(digit)):
                num += digit[i]
        return num

下面来说说大佬们的规律，一个数xyz按位相加有什么规律呢？（xyz代表百位千位和十位）
xyz = 100*x + 10*y + z = 99*x + 99*y + (x+y+z)
x，y，z的最大值可能都是9，所以（x+y+z）之和可能是两位数也可能是一位数。如果是一位数正好就是我们模9的余数，如果是两位数则又变成了
mn = 10*m + n = 9*m + (m+n)
m最大为1 n最大为8 所以（m+n）是一位数，综上xyz按位相加的值就是模9取余的值，到这里原理讲完了，至于4位数5位数同理，接下来看代码吧：

    def addDigits(self, num: int) -> int:
        if (num % 9 == 0) and (num != 0):
            return 9
        else:
            return num % 9

还有一种写法就是我们常见的模10取位，这种方法太常见了不赘述了，看代码吧：

    def addDigits3(self, num: int) -> int:
        while num >= 10:
            sum = 0
            while num > 0:
                sum += num % 10
                num //= 10
            num = sum
        return num

【268】缺失数字
题目要求：给定一个包含 0, 1, 2, …, n 中 n 个数的序列，找出 0 … n 中没有出现在序列中的那个数。
题目解析：简单题的题目都不难理解，期初我写了一个代码但是没有通过，他给我的报错是输入0，但是预期的返回结果是1。起初我有点费解，后来捉摸了一下这个题的意思应该是如果是连续的就要返回比这个集合最大值+1。然后我就改了一版代码，当然这是为了实现，什么都没有考虑，代码如下：

    def missingNumber(self, nums) -> int:
        temp = max(nums) + 1
        for i in range(0, temp):
            if not (i in nums):
                return i
        return temp

这个时间复杂度看似是O(len(nums)-1),但是实际max里面也用了迭代器。所以会慢，优化空间很大，官方给出的答案的第一种和第二种我看过了其实半斤八两，看到哈希set的时候我确实有点触动，因为我确实没有考虑到会有重复的这种情况。因为我一开始的理解就是数字顺序是打乱的但是只是少一个，没想到有没有这种坑，不过这都不重要，因为这不是优化的重点，我写出来只是想让大家知道我当时怎么想的。但是官方的第三种解法我真的是狗生难忘，说句实话我从来没见过，之前刷只是为了刷题不怎么关注题解，这把一看真TM强。反正我当时是没想到，可能是我孤陋寡闻。先说下什么是异或，异或就是两个数不相同则为1，相同为0.例如1异或0为1，0异或0为0，1异或1为1。接下来说第二点，两个相同的数异或一定是0的，因为这两个数的二进制完全相同。第三点是异或是满足结合律的，因为一共n个数我们就把角标和该角标对应的值相互异或，因为少一个数所以最后一定是少的那个数的角标异或0，可以看官方给出的这个图片

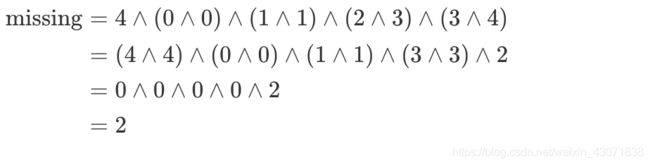
这里2就是确实缺失的数值，因为我们只能获取到角标2但是获取不到值为2的数字。最后就变成了0异或（缺少的的那个值），这里要知道0异或任何数都等于任何数。至此就是这个解法，下面看代码：

    def missingNumber2(self, nums):
        missing = len(nums)
        #i是角标 num是角标对应的值，可能不是一一对应
        for i, num in enumerate(nums):
            missing ^= i ^ num
        return missing

最后一种就是差值法，反正只是少一个就用角标之减去nums这个集合里面元素的和就可以了这里面就不赘述了，真心没难度，代码如下：

    def missingNumber3(self, nums):
        return sum(range(len(nums) + 1)) - sum(nums)

【292】Nim游戏
题目要求：你和你的朋友，两个人一起玩 Nim 游戏：桌子上有一堆石头，每次你们轮流拿掉 1 - 3 块石头。 拿掉最后一块石头的人就是获胜者。你作为先手。编写一个函数，来判断你是否可以在给定石头数量的情况下赢得游戏。
题目解析：说句实话，看到这个题我在那一顿写呀。跟大部分评论的人一样，又是贪心算法又是动态排序。写了一大顿还没调过，后来看了官方答案，dog太阳的。侮辱智商呀，这里就直接讲官方的解法。首先题目的要求是什么情况下我们能赢，我们这个时候就要反着想，什么情况我们会输？这个不难想，就是在你的回合有4块石头你肯定输。为啥？因为你每次能拿1-3块，4块你拿几块你都输。所以总的石头数量绝对不能是4的倍数。这里我要借鉴一个大佬的评论十分精辟

面对4的整数倍的人永远无法翻身，你拿N根对手就会拿4-N根，保证每回合共减4根，你永远对面4倍数，直到4. 相反，如果最开始不是4倍数，你可以拿掉刚好剩下4倍数根，让他永远对面4倍数

然后我们就来将这个代码，首先官方的代码极其简单，不赘述：

    def canWinNim(self, n: int) -> bool:
        return (n % 4) != 0

【下面这个代码是错的！！！】
【下面这个代码是错的！！！】
【下面这个代码是错的！！！】
还有一种形式，我看到采用位运算去进行运算，代码如下：

    def canWinNim2(self, n: int) -> bool:
        return (n & 3) != 0

本文第【342】题有一个结论大家去看一下，那地方讲的很详细。一个数的的n次方减一 一定能整除这个数减一，但是8不是4的幂次方这个要明白，他是整除不了3的。但是这道题像我上面这么写居然可以通过。一定要理解，因为里面有些人写的评论不一定是对的，因为测试用例不全面所以测不出来，我已经补提了这个测试用例。

【326】3的幂
题目要求：给定一个整数，写一个函数来判断它是否是 3 的幂次方。
题目解析：从大意上来看这道题跟231很像，一个是看是否是2的幂次方，一个是看3的幂次方。首先看到这个题的第一个想法，还是采取乘法判断的方法，这是一个求幂次方的通用解法，不赘述直接看代码：

    def isPowerOfThree(self, n: int) -> bool:
        temp = 1
        if n<temp:
            return False
        while n>= temp:
            if n == temp:
                return True
            temp  = temp * 3
        return False

这道题不想2次幂那道有什么过多可以讲的东西，等我看到好的解法我再来补充吧，毕竟LeetCode是一直在刷的。
【342】4的幂
题目要求：给定一个整数 (32 位有符号整数)，请编写一个函数来判断它是否是 4 的幂次方。
题目解析：首先刷过的第一反应就是有个2的幂次方在231题，3的幂次方在326幂次方。总之长得挺像的，在之前两道题我也一直都写过一个特别纯正的结题思路，俗称硬搞，代码如下，不过多赘述，有问题留言：

    def isPowerOfFour(self, num: int) -> bool:
        temp = 1
        if num < temp:
            return False
        while temp <= num:
            if num == temp:
                return True
            temp = temp * 4
        return False

但是吧这个题挺特殊的，大家仔细想一下231题结题时候我发出来的第二种解法，当时说到1<<31现在我们是每个数都要乘4，位运算向左移动移位就是乘1个2，也就是我们每次的移位要向左边移动两位就是连续乘两个2。我想我这么说大家是能理解的。接下来的几种做法希望大家不要喷我，首先既然在整数的范围内总共就是16种可能，为什么是16种？我图个方便我就不写了，看下面这个截图

然后我们来这种暴力的解法，就是一个个匹配，最多也就匹配16次呗，代码如下：

    def isPowerOfFour(self, num: int) -> int:
        temp = [1]
        for i in range(1, 16):
            if num < temp[i - 1]:
                return False
            temp.append(4 ** i)
            if temp[i] == num or num ==1:
                return True
        return False

当然还有种高端的写法，也不叫高端吧就是官方给出的用到了类，代码如下：

class Powers:
    def __init__(self):
        max_power = 15
        self.nums = nums = [1] * (max_power + 1)
        for i in range(1, max_power + 1):
            nums[i] = 4 * nums[i - 1]

class Solution:
    p = Powers()
    def isPowerOfFour(self, num: int) -> bool:
        return num in self.p.nums

现在我们来回归怎么用位运算来解决这个事情，看官方这个解释：

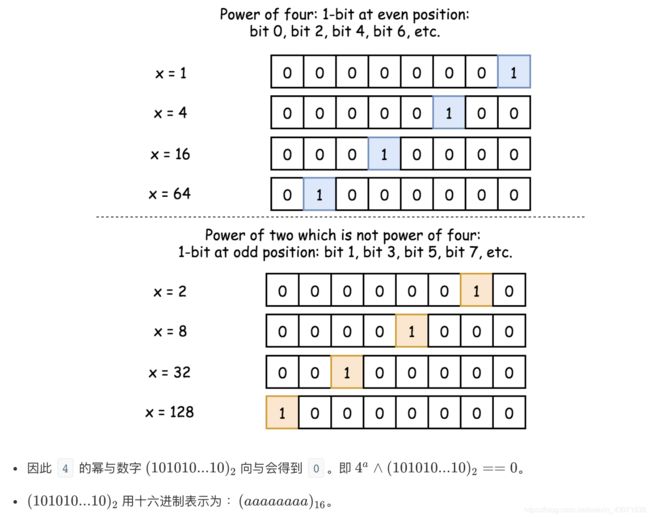
可能有人疑惑哈，为什么与运算之后是0，仔细看4的幂次方的2进制所有的1都在奇数位，而（10101010……）的奇数位都是0，0&1都是0所以才会有这种结果。至此就直接背住这个结论：在该数是2的幂次方的情况下，4的幂次方和（aaaaaaaa）的与运算的结果是0。代码如下：

    def isPowerOfFour4(self,num:int) -> int:
        return num > 0 and num & (num - 1) == 0 and num & 0xaaaaaaaa == 0

当然还有种解法就是按照：num是否小于0 ->判断是不是2的幂次方 ->校验奇数位上是否只有一个1.代码如下：

    def isPowerOfFour5(self, num: int) -> bool:
        if num < 0 or num & (num - 1):
            return False
        return num & 0x55555555;

当然我在评论中有看到有人说最后一句可以换成 num % 3 ==1,这里是可以的为什么呢？其实很简单按照上面的判断逻辑，现在这个数一定是2的幂次方，有可能是2，4，8，16……由于 4=3+1， 那么4的N次方就是（3+1）^N尝试展开多项式，比如(3+1)^2 =(3+1)(3+1)，除了11以外永远都有3相乘，再展开3次方，(3+1)(3+1)(3+1)，结论一致，除了结尾的1都有3相乘，因此可以有结论，一个数的N次方减1总能除尽比这个数小1的数。
其实还有一种解法就是官方的那种数学解法，巧妙地运用了log，这里不赘述了因为方法太多了，我主要想留底的就是这个位运算，因为很多人不太理解，所以也追加到我的博文中。