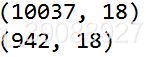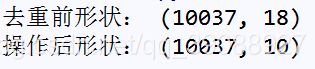数据预处理之数据清洗
数据预处理之数据清洗
清洗重复数据
重复数据分为记录重复和特征重复,记录重复是指出现多条数据相同的情况;特征重复是指对于同一张表格中的两列不同名数据,其对于整个数据分析产生的影响都是雷同的,这两列数据被称为特征重复数据。
记录重复
对于记录重复,我们有三种方法进行去重:
import pandas as pd
data=pd.read_csv('f:/data/detail.csv',index_col=0,encoding='gbk')
#方法一
def delRep(list1):
list2=[]
for i in list1:
if i not in list2:
list2.append(i)
return list2
dishes=list(data['dishes_name']) #将菜名提取出来,并转化为列表
print("去重前菜品总数:",len(dishes))
dish=delRep(dishes) #使用自定义函数去重
#方法二
dishes=list(data['dishes_name']) #将菜名提取出来,并转化为列表
print("去重前菜品总数:",len(dishes))
dish=set(dishes) #使用Set去重,虽然简单,但会导致数据排序发生改变
#方法三,一般使用该方法进行去重
dish_name=data['dishes_name'].drop_duplicates()
#方法三也可以对多列进行去重
print(data.shape)
shapeSet=data.drop_duplicates(subset=['order_id','emp_id'])
print(shapeSet.shape)
特征去重
去除连续的特征重复,可以利用特征之间的相似度将将2个相似度为1的特征去除一个,相似度计算方法为corr,默认为皮尔逊相似度,可以通过method方法调节,还支持spearman法和kendall法。
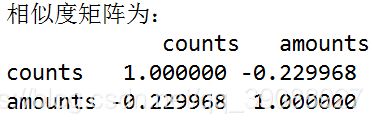
corrDet=data[['counts','amounts']].corr(method='kendall')
print('相似度矩阵为:\n',corrDet)
结果:
注意:该方法只能对数值型重复特征进行去重,而类别特征之间无法通过相似系数来衡量相似度
另外还有DataFrame.equals的方法可以去重,该方法为常用方法:
import pandas as pd
data = pd.read_csv('f:/data/detail.csv', index_col=0, encoding='gbk')
print('去重前形状:', data.shape)
# 样本去重
data.drop_duplicates(inplace=True) # inplace=True表示在原表上进行操作
# 特征去重
def FeatureEquals(df):
# 定义求取特征是否完全相同的矩阵的函数
dfEquals = pd.DataFrame([], columns=df.columns, index=df.columns)
for i in df.columns:
for j in df.columns:
dfEquals.loc[i, j] = df.loc[:, i].equals(df.loc[:, j])
return dfEquals
detEquals = FeatureEquals(data)
# 遍历所有数据
lenDet = detEquals.shape[0]
dupCol = []
for k in range(lenDet):
for l in range(k + 1, lenDet):
if detEquals.iloc[k, l] & (detEquals.columns[l] not in dupCol):
dupCol.append(detEquals.columns[l])
#删除重复列
data.drop(dupCol,axis=1,inplace=True)
print('操作后形状:',data.shape)
异常值处理
异常值是指数据中的个别数据明显偏离其余的数值,也称为离群点。
拉依达准则
只对正态分布或近似正态分布数据有效,而对于其他分布数据无效。实现代码:
import pandas as pd
import numpy as np
data = pd.read_csv('f:/data/detail.csv', index_col=0, encoding='gbk')
def outRange(Serl):
boolInd = (Serl.mean() - 3 * Serl.std() > Serl) | \
(Serl.mean() + 3 * Serl.std() < Serl)
# 通过法则返回异常值索引
index = np.arange(Serl.shape[0])[boolInd]
outrange = Serl.iloc[index]
return outrange
outlier = outRange(data['counts'])
print("异常值个数:", outlier.shape[0])
print("异常值最大为:", outlier.max())
print("异常值最小为:", outlier.min())
print("异常值为:\n", outlier)
箱线图分析:
异常值通常被定义为QL-1.5IQR或大于QU+1.5IQR的,QL为下四分位数,QU为上四分位数,IQR为四分位数间距,是上下四分位数之差,包含了全部观察值的一半。箱线图较为直观,没有对数据有任何要求,判断标准以四分位数和四分位数间距为基础。
实现代码:
plt.figure(figsize=(10, 8))
p = plt.boxplot(data['counts'].values, notch=True) # 画出箱线图
outlier = p['fliers'][0].get_ydata() # fliers为异常值的标签
plt.show()
print(outlier)
print(len(outlier))
print(outlier.max())
print(outlier.min())
检测与处理缺失值
import pandas as pd
data = pd.read_csv("f:/data/detail.csv", index_col=0, encoding='gbk')
# 每个特征的缺失数目
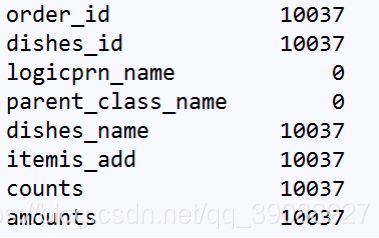
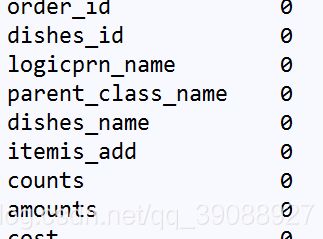
print(data.notnull().sum())
# how取值为any时,删除了一个特征,说明这个特征存在缺失值。
# 若how参数不取any这个默认值,而取all,则表示整个特征全为缺失值时才删除
print('删除缺失列前detail的形状为:', data.shape)
print('删除缺失列后detail的形状为:', data.dropna(axis=1, how='any').shape)

缺失值为数值型,通常利用其均值、中位数和众数等来替代缺失值;缺失值为类别型时,则选用众数来进行替
#将缺失值用-99进行替换,缺失值已不存在
data=data.fillna(-99)
print(data.isnull().sum())
删除法简单,但会因其数据结构变化,样本减少;替换法使用难度较低,但会影响数据的标准差,会导致数据的信息变动。常用的插值法有线性插值、多项式差值和样条插值。线性插值根据已知值求出线性方程,通过线性方程得到缺失值。多项式插值是利用已知的值拟合出一个多项式,使得现有的数据满足这个多项式,再利用多项式求解缺失值。样条插值是以可变样条来做出一条经过一系列点的光化曲线的插值方法。
实现代码:
# 线性插值
import numpy as np
from scipy.interpolate import interp1d
x = np.array([1, 2, 3, 4, 5, 8, 9, 10]) # 创建自变量
y1 = np.array([2, 8, 18, 32, 50, 128, 162, 200]) # 创建因变量y1
y2 = np.array([3, 5, 7, 9, 11, 17, 19, 21]) # 创建因变量y2
LinearValue1 = interp1d(x, y1, kind='linear') # 线性插值拟合x、y1
LinearValue2 = interp1d(x, y2, kind='linear') # 线性插值拟合x、y2
print('当x为6、7时,使用线性插值y1为', LinearValue1([6, 7]))
print('当x为6、7时,使用线性插值y2为', LinearValue2([6, 7]))
# 拉格朗日插值
from scipy.interpolate import lagrange
LargeValue1 = lagrange(x, y1)
LargeValue2 = lagrange(x, y2)
print('当x为6、7时,使用拉格朗日插值y1为', LargeValue1([6, 7]))
print('当x为6、7时,使用拉格朗日插值y2为', LargeValue2([6, 7]))
# 样条插值
from scipy.interpolate import spline
# 样条插值拟合x,y1
SplineValue1 = spline(x, y1, xnew=np.array([6, 7]))
# 样条插值拟合x,y2
SplineValue2 = spline(x, y2, xnew=np.array([6, 7]))
print('当x为6、7时,使用样条插值y1为', SplineValue1)
print('当x为6、7时,使用样条插值y2为', SplineValue2)

从拟合结果来看,多项式插值法和样条插值结果都较为出色,而线性插值仅仅在自变量和因变量之间存在线性关系时才较为出色,所以平时使用多项式插值和样条插值较多。