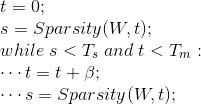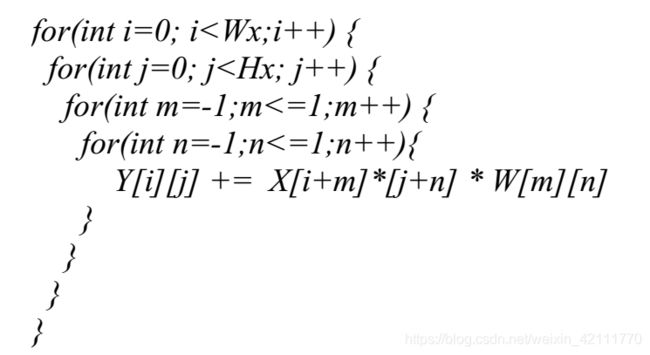卷积网络的稀疏与量化

论文: Sparse, Quantized, Full Frame CNN for Low Power Embedded Devices

github: https://github.com/tidsp/caffe-jacinto

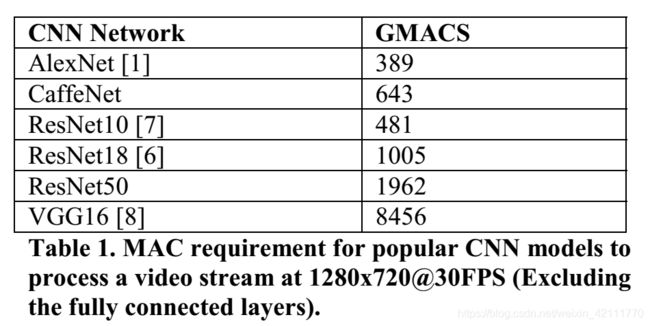
AI爆发的三个条件，算法，算力和数据。深度学习对算力要求极高，如果没有一块性能良好的GPU，那么模型训练和调参将是一件耗时的工作，严重拖慢工作进度。CNN因为其高效的特征提取和参数共享机制使得其在图像处理方面表现优异，下面介绍了经典的的CNN网络架构处理1280x720@30FPS的视频流所需的计算量。

一个 GMACS等于每秒10亿 (=10^9) 次的定点乘累加运算

将CNN模型运行在DSPs上所需的计算复杂度需要低于50GMACS，由上表所知，CNN模型所需的计算复杂度远远高于DSP的要求，那么要如何才能降低CNN模型的复杂度，使其运行在DSPs上呢？

存在多种方法能够降低CNN的复杂度，早先的方法有用可分的卷积代替不可分的卷积，这种方法提速4.5x，精度降低1%，这种方法的缺点是需要更改网络架构，将一层拆分成水平和垂直的过滤器；还有一种能够不更改网络架构也能稀疏卷积的算法，这种算法在训练过程中定义高的权重衰减，当权重的绝对值低于预先定义的阈值时，二值化为0。固定为0的参数，fine-tune非0的参数，以此来恢复因稀疏降低的准确率；将浮点精度的系数量化为Dynamic 8比特的顶点也是一种有效的方法。

在这篇论文中，为了降低CNN的计算复杂度，作者提出了如下四步操作：

• a quick sparsification method 
• fine-tuning without loss of sparsity
• low complexity dynamic 8-bit quantization
• Sparse convolution method to speedup inference

快速稀疏

在网络训练中，添加L1正则化有助于稀疏的稀疏化，所以第一步就是在网络训练中增加一个高权重衰减值的L1正则化。

接下来，假设为某一层的稀疏目标值，是这一层中为0的权重个数占总权重个数的比率，每一层的稀疏目标值可以设置不同；设为这一层权重的绝对值最大值；设为最大阈值，;设为这一层的权重张量，那么

                                                                 

从一个很小的稀疏阈值t开始，计算在当前阈值下的稀疏率s，如果s小于设定的稀疏目标值并且t小于设定的最大阈值，为当前的稀疏阈值t增添一个很小的增量(一般取1e-7)，然后计算新稀疏阈值下的稀疏率s，以此循坏，直至while循环里面的条件不被满足。

Sparsity()函数计算给定稀疏阈值t，参数向量中稀疏的绝对值小于t的稀疏的比率。

微调

上述步骤中的阈值计算会降低CNN模型的准确率，进过微调之后可以恢复降低的准确率。在量化初期，构造由非0稀疏组成的map，然后在整个微调期间，仅仅更新这些非0系数值，为0的稀疏值保持不变。

量化

研究表明，将浮点精度的稀疏量化到动态的8比特定点(Dynamic 8-bit fixed point)能够保持图像分类问题的准确率，"Dynamic"在这里指的是CNN层与层之间的量化乘积因子(quantization multiplication factor)，量化边界是不同的，框架之间也是不同的。

在训练期间，Exponential moving averages被用于计算每批训练数据在各层中的不同张量(权重，输入和输出)的最大值和最小值。Flags被插入CNN模型中用来表示哪些张量是有符号的，哪些是无符号的。对于有符号的张量，被量化到-128到127之间；对于无符号的张量，被量化至0至255之间。在论文中，作者限制了量化乘积因子必须是2的倍数。

假如张量的边界值为和, 无符号张量的整型长度(Integer length)为; 有符号张量的整型长度为

, 那么fractional length 被计算为 ; 张量的量化乘积因子为。

张量通过乘以量化乘积因子被量化，然而一些值可能处在边界值之外，所以就不得不被裁剪clip。对于无符号张量，

对于有符号张量

卷积稀疏计算

假设X为输入张量，Y为输出张量，W为权重张量，Wx和Hx为输入张量的宽和高，那么关于一个3x3的卷积运算伪代码如下所示：

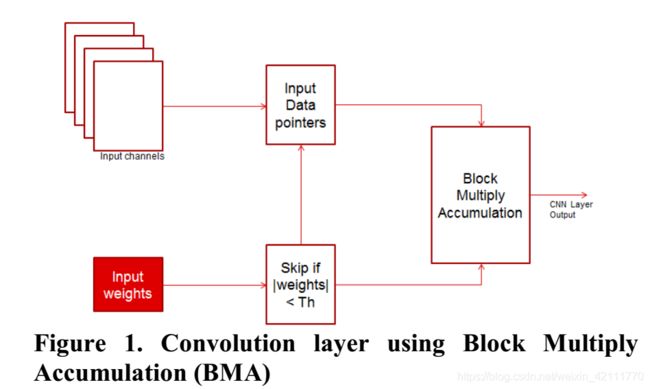
将上述代码里面的循环可以被调换顺序，将内循环调到外面，这样每一次整个block都乘以一个单独的权重值，一次计算整个block，好处在于权重为0的时候，整个block就能够被跳过，这样的卷积计算方式被称为Block Multiply Accumulation(BMA)。

                                                            

如果应用BMA计算整个卷积层，首先需要收集非零权重所对应的block指针，然后将非零权重和相应的输入和输出指针收集在单独的列表中。BMAlist()函数从xList函数中取出一个块指针，从wList中取出一个权重值，相乘，然后累积整个块到yList的指针。伪代码如下（本人认为以下的伪代码仅仅计算了输出p个通道的第[0][0]值).

使用BMA的卷积计算如下图所示：

Implementation on device

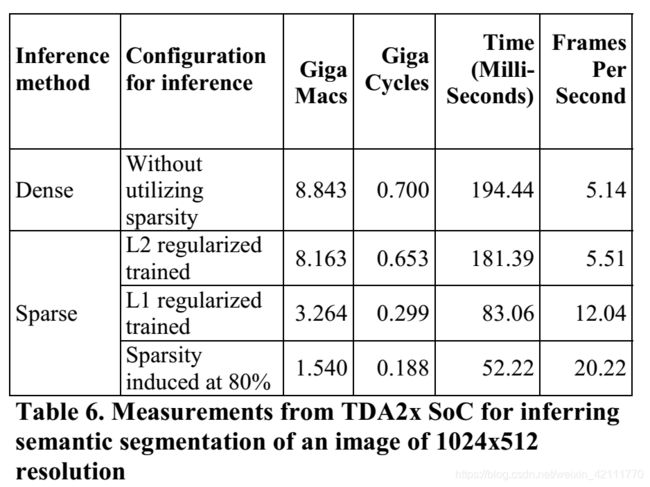
稀疏的卷积网络被应用在Texas instruments的TDA2x SoC，它有四个EVE。以下表格比较了了JSegNet21 CNN网络的稠密格式和它相应稀疏格式在处理1024x512图像分割的复杂度。