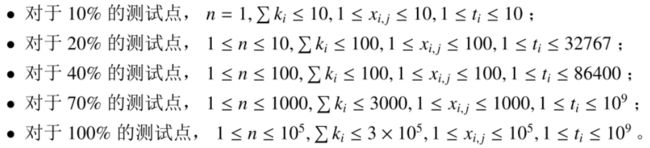NOIP 2016 普及组
文章目录
- T1 买铅笔
-
- T1分析
- T2 回文日期
-
- T2分析
- T3 海港
-
- T3分析
- T4 魔法阵
-
- T4分析
T1 买铅笔
题目点击→计蒜客 [NOIP2016]买铅笔
题目描述
P 老师需要去商店买 n n n 支铅笔作为小朋友们参加 NOIP 的礼物。她发现商店一共有 3 3 3 种包装的铅笔,不同包装内的铅笔数量有可能不同,价格也有可能不同。为了公平起见,P老师决定只买同一种包装的铅笔。
商店不允许将铅笔的包装拆开,因此 P 老师可能需要购买超过 n n n 支铅笔才够给小朋友们发礼物。
现在 P 老师想知道,在商店每种包装的数量都足够的情况下,要买够至少 n n n 支铅笔最少需要花费多少钱。
输入格式
第一行包含一个正整数 n n n ,表示需要的铅笔数量。
接下来三行,每行用 2 2 2 个正整数描述一种包装的铅笔:其中第 1 1 1 个整数表示这种 包装内铅笔的数量,第 2 2 2 个整数表示这种包装的价格。
保证所有的 7 7 7 个数都是不超过 10000 10000 10000 的正整数。
输出格式
1 1 1 个整数,表示 P P P 老师最少需要花费的钱。
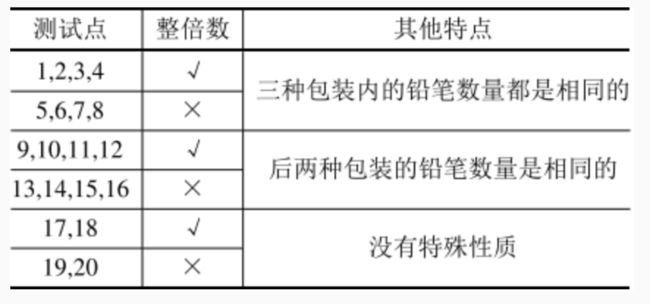
数据范围
样例说明
样例1:
铅笔的三种包装分别是:
2 2 2 支装,价格为 2 2 2 ;
50 50 50 支装,价格为 30 30 30 ;
30 30 30 支装,价格为 27 27 27 。
P老师需要购买至少 57 57 57 支铅笔。
如果她选择购买第一种包装,那么她需要购买 29 29 29 份,共计 2 × 29 = 58 2 \times 29 = 58 2×29=58 支,需要花 费的钱为 $2 \times 29 = 58 $。
实际上, P 老师会选择购买第三种包装,这样需要买 2 2 2 份。虽然最后买到的铅笔数量更多了,为 30 × 2 = 60 30 \times 2 = 60 30×2=60 支,但花费却减少为 27 × 2 = 54 27 \times 2 = 54 27×2=54 ,比第一种少。
对于第二种包装,虽然每支铅笔的价格是最低的,但要够发必须买 2 2 2 份,实际的花费达到了 30 × 2 = 60 30 \times 2 = 60 30×2=60 ,因此 P 老师也不会选择。
所以最后输出的答案是 54 54 54 。
T1分析
送分题,直接通过数学计算,所有的钱买这个笔可以买多少个。然后取个最小值就可以了。
#include
#include
using namespace std;
const int inf = 0x3f3f3f3f;
int main(){
int n, a, b, mi = inf;
cin >> n;
for (int i = 0; i < 3; i++) {
cin >> a >> b;
mi = min(mi, (int)ceil(n * 1.0 / a) * b);
}
cout << mi << endl;
return 0;
}
T2 回文日期
题目点击→计蒜客 [NOIP2016] 回文日期
题目描述
在日常生活中,通过年、月、日这三个要素可以表示出一个唯一确定的日期。
牛牛习惯用 8 8 8 位数字表示一个日期,其中,前 4 4 4 位代表年份,接下来 2 2 2 位代表月份,最后 2 2 2 位代表日期。显然:一个日期只有一种表示方法,而两个不同的日期的表示方法不会相同。
牛牛认为,一个日期是回文的,当且仅当表示这个日期的 8 8 8 位数字是回文的。现 在,牛牛想知道:在他指定的两个日期之间包含这两个日期本身),有多少个真实存在的日期是回文的。
一个 8 8 8 位数字是回文的,当且仅当对于所有的i ( 1 ≤ i ≤ 8 1 \le i \le 8 1≤i≤8 )从左向右数的第 i i i 个 数字和第 9 − i 9-i 9−i 个数字(即从右向左数的第 i i i 个数字)是相同的。
例如:
-
对于 2016 2016 2016 年 11 11 11 月 19 19 19 日,用 8 8 8 位数字 20161119 20161119 20161119 表示,它不是回文的。
-
对于 2010 2010 2010 年 1 1 1 月 2 2 2 日,用 8 8 8 位数字 20100102 20100102 20100102 表示,它是回文的。
-
对于 2010 2010 2010 年 10 10 10 月 2 2 2 日,用 8 8 8 位数字 20101002 20101002 20101002 表示,它不是回文的。
每一年中都有 12 12 12 个月份:
其中, 1 1 1、 3 3 3、 5 5 5、 7 7 7、 8 8 8、 10 10 10、 12 12 12 月每个月有 31 31 31 天; 4 4 4、 6 6 6、 9 9 9、 11 11 11 月每个月有 30 30 30 天;而对于 2 2 2 月,闰年时有 29 29 29 天,平年时有 28 28 28天。
一个年份是闰年当且仅当它满足下列两种情况其中的一种:
-
这个年份是 4 4 4 的整数倍,但不是 100 100 100 的整数倍;
-
这个年份是 400 400 400 的整数倍。
例如:
-
以下几个年份都是闰年: 2000 2000 2000、 2012 2012 2012、 2016 2016 2016。
-
以下几个年份是平年: 1900 1900 1900、 2011 2011 2011、 2014 2014 2014。
输入格式
输入包括两行,每行包括一个 8 8 8 位数字。
第一行表示牛牛指定的起始日期。
第二行表示牛牛指定的终止日期。
保证 d a t e i date_i datei 和都是真实存在的日期,且年份部分一定为 4 4 4 位数字,且首位数字不为 0 0 0 。
保证 d a t e 1 date_1 date1 —定不晚于 d a t e 2 date_2 date2 。
输出格式
输出一行,包含一个整数,表示在 d a t e 1 date_1 date1 和 d a t e 2 date_2 date2 之间,有多少个日期是回文的。
数据范围
对于 60 % 60\% 60% 的数据,满足 d a t e 1 = d a t e 2 date_1 = date_2 date1=date2。
样例解释
样例1:
符合条件的日期是 20111102 20111102 20111102。
样例2:
符合条件的日期是 20011002 20011002 20011002 和 20100102 20100102 20100102。
T2分析
枚举后四位然后求出整个日期,判断是否在范围内即可。
2 2 2 月不需要判断是否是闰年,因为 0229 0229 0229 反过来是 9220 9220 9220 ,整个日期是 92200229 92200229 92200229 ,而 9220 9220 9220 年是闰年。
#include
using namespace std;
int d[] = {0, 31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
int main(){
int n, m, tmp, sum = 0;
cin >> n >> m;
for(int i = 1; i <= 12; i++){
for(int j = 1; j <= d[i]; j++){
tmp = ((j % 10) * 1000+ (j /10) * 100+ (i % 10) * 10 + (i / 10)) * 10000 + i * 100 + j;
if(tmp >= n && tmp <= m){
sum++;
}
}
}
cout << sum << endl;
return 0;
}
T3 海港
题目点击→ 计蒜客 [NOIP2016]海港
题目描述
小 K 是一个海港的海关工作人员,每天都有许多船只到达海港,船上通常有很多来自不同国家的乘客。
小K对这些到达海港的船只非常感兴趣,他按照时间记录下了到达海港的每一艘船只情况;对于第 i i i 艘到达的船,他记录了这艘船到达的时间 t i t_i ti (单位:秒),船上的乘客数 k i k_i ki ,以及每名乘客的国籍 x i , 1 , x i , 2 , … , x i , k i x_i,1, x_i,2,…,x_i,k_i xi,1,xi,2,…,xi,ki。
小 K 统计了 n n n 艘船的信息,希望你帮忙计算出以每一艘船到达时间为止的 24 24 24 小时( 24 24 24 小时= 86400 86400 86400 秒)内所有乘船到达的乘客来自多少个不同的国家。
形式化地讲,你需要计算 n n n 条信息。对于输出的第 i i i 条信息,你需要统计满足 t i − 86400 < t p ≤ t i t_i - 86400 < tp \le t_i ti−86400<tp≤ti 的船只 p p p,在所有的 x p , j x_{p,j} xp,j 中,总共有多少个不同的数。
输入格式
第一行输入一个正整数 n n n,表示小 K 统计了 n n n 艘船的信息。
接下来 n n n 行,每行描述一艘船的信息:前两个整数 t i t_i ti 和 k i k_i ki 分别表示这艘船到达海港的时间和船上的乘客数量,接下来 k i k_i ki 个整数 x ( i , j ) x(i,j) x(i,j) 表示船上乘客的国籍。
保证输入的 t i t_i ti 是递增的,单位是秒;表示从小 K 第一次上班开始计时,这艘船在第 t i t_i ti 秒到达海港。
保证 1 ≤ n ≤ 1 0 5 1 \le n \le 10^5 1≤n≤105, ∑ k i ≤ 3 × 1 0 5 \sum k_i \le 3 \times 10^5 ∑ki≤3×105, 1 ≤ x ( i , j ) ≤ 1 0 5 1 \le x(i,j) \le 10^5 1≤x(i,j)≤105, 1 ≤ t ( i − 1 ) ≤ t i ≤ 1 0 9 1 \le t(i-1) \le t_i \le 10^9 1≤t(i−1)≤ti≤109。
其中 ∑ k i \sum k_i ∑ki 表示所有的 k i k_i ki 的和。
输出格式
输出 n n n 行,第 i i i 行输出一个整数表示第 i i i 艘船到达后的统计信息。
样例说明
样例1:
第一艘船在第 1 1 1 秒到达海港,最近 24 24 24 小时到达的船是第一艘船,共有 4 4 4 个乘客,分别是来自国家 4 , 1 , 2 , 2 4,1,2,2 4,1,2,2,共来自 3 3 3 个不同的国家;
第二艘船在第 2 2 2 秒到达海港,最近 24 24 24 小时到达的船是第一艘船和第二艘船,共有 4 + 2 = 6 4 + 2 = 6 4+2=6 个乘客,分别是来自国家 4 , 1 , 2 , 2 , 2 , 3 4,1,2,2,2,3 4,1,2,2,2,3 ,共来自 4 4 4 个不同的国家;
第三艘船在第 10 10 10 秒到达海港,最近 24 24 24 小时到达的船是第一艘船、第二艘船和第三艘船,共有 4 + 2 + 1 = 7 4+2+1=7 4+2+1=7 个乘客,分别是来自国家 4 , 1 , 2 , 2 , 2 , 3 , 3 4,1,2,2,2,3,3 4,1,2,2,2,3,3,共来自 4 4 4 个不同的国家。
样例2:
第一艘船在第 1 1 1 秒到达海港,最近 24 24 24 小时到达的船是第一艘船,共有 4 4 4 个乘客,分别是来自国家 1 , 2 , 2 , 3 1,2,2,3 1,2,2,3,共来自 3 3 3 个不同的国家。
第二艘船在第 3 3 3 秒到达海港,最近 24 24 24 小时到达的船是第一艘船和第二艘船,共有 4 + 2 = 6 4+2=6 4+2=6 个乘客,分别是来自国家 1 , 2 , 2 , 3 , 2 , 3 1,2,2,3,2,3 1,2,2,3,2,3,共来自 3 3 3 个不同的国家。
第三艘船在第 86401 86401 86401 秒到达海港,最近 24 24 24 小时到达的船是第二艘船和第三艘船,共有 2 + 2 = 4 2+2=4 2+2=4 个乘客,分别是来自国家 2 , 3 , 3 , 4 2,3,3,4 2,3,3,4,共来自 3 3 3 个不同的国家。
第四艘船在第 86402 86402 86402 秒到达海港,最近 24 24 24 小时到达的船是第二艘船、第三艘船和第四艘船,共有 2 + 2 + 1 = 5 2+2+1=5 2+2+1=5 个乘客,分别是来自国家 2 , 3 , 3 , 4 , 5 2,3,3,4,5 2,3,3,4,5,共来自 4 4 4 个不同的国家。
T3分析
40 % 40\% 40% 分的数据比较简单,所有人必然在 24 24 24 小时内,那就只需要记录一下前缀有多少个不同的国家就可以了,这非常简单
到这里我们可以观察数据范围,我们可以发现数据范围中最显眼的一点的就是 k k k ,数据保证的是 ∑ k \sum k ∑k 的范围,那其实这也是在提示我们,这道题思考的关键点在于总人数!我们可以从单个人下手去实现这道题
70 % 70\% 70% 分的数据要在 40 % 40\% 40% 的基础上考虑时间的问题,但是可以发现,总人数是不多的,所以只要不是什么复杂的暴力,也可以获得这部分分数
100 % 100\% 100% 的数据,其实我们手动模拟一下就可以发现,因为输入顺序是按照到达时间来的,所以我们要做的就是,当一个人呆的时间超过 24 h 24h 24h 这个人就没用了,就可以删掉了
那再换一个思路,我们非要这个人到了 24 h 24h 24h 就立刻删掉他吗? 显然不用,在下一次询问之前,这个人一直呆在序列里也是没关系的,所以我们只要在每艘船到来的时候,把离这艘船超过 24 h 24h 24h 的人全部删除即可,而且我们可以发现,删除的必然是到来序列中前面一段人,因为到来时间是按顺序的
那其实就可以发现,这就是一个从一端添加元素,从另一端删除元素的结构,那这不就是 队列 吗?
所以我们可以建立一个队列,队列里面存储每一个人的到达时间和他的国籍。用一个计数器记录过去 86400 86400 86400 秒内出现的国家个数。
每一艘船只到达时,从队头开始扫描,如果到达时间大于等于 86400 86400 86400 就出队,并且对应国籍人数减去一,如果这个国家没人了,计数器减去一。然后将那艘船只上面的人加入队尾,并且并且对应国籍人数加一,如果之前这个国家没人,计数器加一。然后输出当前计数器的结果即可。
#include
#include
#include
#include
#include
#include
using namespace std;
int a[100100];
int people[500100];
struct node{
int country;
int time;
};
queueq;
int main(){
int n, sum = 0;
scanf("%d", &n);
for(int i = 1; i <= n; i++){
int t, p;
scanf("%d%d", &t, &p);
node temp;
temp.time = t;
for(int i = 1; i <= p; i++){
int cty;
scanf("%d", &cty);
temp.country = cty;
q.push(temp);
if(!people[cty]){
sum++;
}
people[cty]++;
}
while(1){
node old;
old = q.front();
if(temp.time - 86400 >= old.time){
int tc = old.country;
people[tc]--;
if(!people[tc]){
sum--;
}
q.pop();
} else {
break;
}
}
printf("%d\n", sum);
}
return 0;
}
T4 魔法阵
点击查看→ 计蒜客 [NOIP2016] 魔法阵
题目描述
六十年一次的魔法战争就要开始了,大魔法师准备从附近的魔法场中汲取魔法能量。
大魔法师有 m m m 个魔法物品,编号分别为 1 , 2 , . . . , m 1,2,...,m 1,2,...,m 。每个物品具有一个魔法值,我们用 x i x_i xi 表示编号为 i i i 的物品的魔法值。每个魔法值 x i x_i xi 是不超过 n n n 的正整数,可能有多个物品的魔法值相同。
大魔法师认为,当且仅当四个编号为 a , b , c , d a,b,c,d a,b,c,d 的魔法物品满足 x a < x b < x c < x d x_a
现在,大魔法师想要知道,对于每个魔法物品,作为某个魔法阵的 A A A 物品出现的次数,作为 B B B 物品的次数,作为 C C C 物品的次数,和作为 D D D 物品的次数。
输入格式
输入文件的第一行包含两个空格隔开的正整数 n n n 和 m m m 。
接下来 m m m 行,每行一个正整数,第 i + 1 i+1 i+1 行的正整数表示 x i x_i xi ,即编号为 i i i 的物品的魔法值。
保证 1 ≤ n ≤ 15000 1 \le n \le 15000 1≤n≤15000 , 1 ≤ m ≤ 40000 1 \le m \le 40000 1≤m≤40000 , 1 ≤ X i ≤ n 1 \le X_i \le n 1≤Xi≤n 。每个 x i x_i xi 是分别在合法范围内等概率随机生成的。
输出格式
共输出 m m m 行,每行四个整数。第 i i i 行的四个整数依次表示编号为 i i i 的物品作 为 A A A , B B B , C C C , D D D 物品分别出现的次数。
保证标准输出中的每个数都不会超过 1 0 9 10^9 109 。
每行相邻的两个数之间用恰好一个空格隔开。
数据范围
样例说明
样例1:
共有 5 5 5 个魔法阵,分别为:
物品 1 , 3 , 7 , 6 1,3,7,6 1,3,7,6 ,其魔法值分别为 1 , 7 , 26 , 29 1,7,26,29 1,7,26,29;
物品 1 , 5 , 2 , 7 1,5,2,7 1,5,2,7 ,其魔法值分别为 1 , 5 , 24 , 26 1,5,24,26 1,5,24,26;
物品 1 , 5 , 7 , 4 1,5,7,4 1,5,7,4 ,其魔法值分别为 1 , 5 , 26 , 28 1,5,26,28 1,5,26,28;
物品 1 , 5 , 8 , 7 1,5,8,7 1,5,8,7,其魔法值分别为 1 , 5 , 24 , 26 1,5,24,26 1,5,24,26;
物品 5 , 3 , 4 , 6 5,3,4,6 5,3,4,6,其魔法值分别为 5 , 7 , 28 , 29 5,7,28,29 5,7,28,29。
以物品 5 5 5 为例,它作为 A A A 物品出现了 1 1 1 次,作为 B B B 物品出现了 3 3 3 次,没有作为 C C C 物品或者 D D D 物品出现,所以这一行输出的四个数依次为 1 , 3 , 0 , 0 1,3,0,0 1,3,0,0 。
此外,如果我们将输出看作一个 m m m 行 4 4 4 列的矩阵,那么每一列上的 m m m 个数之和都应等于魔法阵的总数。所以,如果你的输出不满足这个性质,那么这个输出一定不正确。你可以通过这个性质在一定程度上检查你的输出的正确性。
T4分析
暴力可以获得大概 30 % 30\% 30% 的分数, O ( m 4 ) O(m^4) O(m4) 直接枚举四个物品
但是上面这种暴力并不需要 n n n ,那 n n n 不可能作为一个无意义的数据范围,而且可以发现 n n n 还比 m m m 小,所以这里其实是在提示我们,可以往数值上考虑,而不是单独考虑每个物品
观察题目中给出的公式,魔法阵需要满足两个条件
- a < b < c < d a < b < c < d a<b<c<d
- b − a = 2 ( d − c ) b - a = 2(d - c) b−a=2(d−c)
- b − a < ( c − b ) / 3 b - a < (c - b) / 3 b−a<(c−b)/3
那么我们设 d − c = i d - c = i d−c=i 可以得到 b − a = 2 ∗ i b - a = 2 * i b−a=2∗i
再代入第三个条件可以得到 2 ∗ i < ( c − b ) / 3 2 * i < (c - b) / 3 2∗i<(c−b)/3 化简得到 6 ∗ i < c − b 6 * i < c - b 6∗i<c−b
那么必然存在 正整数 k k k 使得 6 ∗ i + k = c − b 6 * i + k = c - b 6∗i+k=c−b,这里注意 k k k 必然是 正整数
将 a , b , c , d a,b,c,d a,b,c,d 画在一个数轴上可以得到下面这个图,这会更加方便我们化简公式
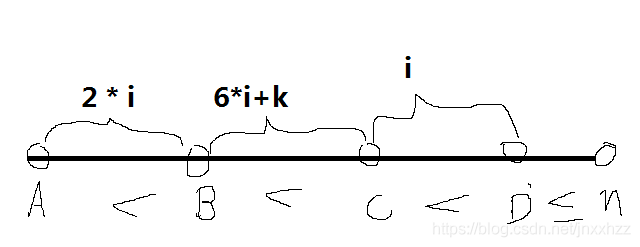
到这里我们可以发现
只要枚举 a a a 和 i i i 就可以得到 b = a + 2 ∗ i b = a + 2 * i b=a+2∗i,
再枚举 k k k 就可以得到 c = b + 6 ∗ i + k = a + 8 ∗ i + k c = b + 6 * i + k = a + 8 * i + k c=b+6∗i+k=a+8∗i+k 和 d = c + i = a + 9 ∗ i + k d = c + i = a + 9 * i + k d=c+i=a+9∗i+k
那么枚举 a a a 不用说了非常简单, i i i 的范围该怎么求呢? 注意图上最后一个条件 ≤ n \leq n ≤n 那我们可以得到 a , b , c , d ≤ n a,b,c,d \leq n a,b,c,d≤n 代入上述式子可以得到 d − a = 9 ∗ i + k d - a = 9 * i + k d−a=9∗i+k 这里因为 k k k 是正整数也就是说 k ≥ 1 k \geq 1 k≥1, 那么 i i i 的范围即为 1 ≤ i ≤ ( n − a − 1 ) / 9 1 \leq i \leq (n-a-1) / 9 1≤i≤(n−a−1)/9
同理 k k k 的范围也可以得到就是 1 ≤ k ≤ n − a − 9 ∗ i 1 \leq k\leq n-a-9*i 1≤k≤n−a−9∗i
这种做法可以得到 80 ∼ 85 80 \sim 85 80∼85 的分数
上面这种做法慢在什么地方呢?显然有一点一定是慢的——我们的方案数是一个个算的
那我们接下来考虑的一定就是如何不再一个个算方案数,而用乘法去算方案数
我们可以在上述计算中,最重要的部分其实是 i i i,那我们接下来就首先枚举 i i i
有了 i i i 以后我们必然是枚举 a a a 或者 d d d 就可以确定第二个点的值了,那这里我们优先枚举 d d d
当然其实枚举 a a a 和 d d d 并没有区别,但是这里为了后面的方便计算,我们枚举 d d d
确定了 d , i d,i d,i 后, c c c 也就可以得到了,接下来我们要做的就是枚举 k k k 去计算 a , b a,b a,b 的数量
这里我们可以发现,当因为 k k k 是正整数,也就意味着当前有了 d d d 以后我们可以计算出离 d d d 最近的那个 m a x a = d − ( 9 ∗ i + 1 ) maxa = d - (9 * i + 1) maxa=d−(9∗i+1),只要是所有小于这个 m a x a maxa maxa 的 a a a 都是合法的,那么对应的就可以得到下面两个计算式
当 前 c 的 方 案 种 数 = ( 当 前 魔 法 值 等 于 d 的 魔 法 物 品 总 量 ) ∗ ( 前 面 得 到 的 若 干 个 a 的 魔 法 物 品 总 量 ) ∗ ( 前 面 得 到 的 若 干 个 b 的 魔 法 物 品 总 量 ) 当前 c 的方案种数 = (当前魔法值等于d的魔法物品总量) * (前面得到的若干个a 的魔法物品总量)*(前面得到的若干个b 的魔法物品总量) 当前c的方案种数=(当前魔法值等于d的魔法物品总量)∗(前面得到的若干个a的魔法物品总量)∗(前面得到的若干个b的魔法物品总量)
当 前 d 的 方 案 种 数 = ( 当 前 魔 法 值 等 于 c 的 魔 法 物 品 总 量 ) ∗ ( 前 面 得 到 的 若 干 个 a 的 魔 法 物 品 总 量 ) ∗ ( 前 面 得 到 的 若 干 个 b 的 魔 法 物 品 总 量 ) 当前d的方案种数=(当前魔法值等于c的魔法物品总量)*(前面得到的若干个a 的魔法物品总量)*(前面得到的若干个b 的魔法物品总量) 当前d的方案种数=(当前魔法值等于c的魔法物品总量)∗(前面得到的若干个a的魔法物品总量)∗(前面得到的若干个b的魔法物品总量)
这里我们可以发现,其实这个 a ∗ b a * b a∗b 的方案数是一个 前缀和,所以我们从左往右枚举 d d d 的同时对 a ∗ b a * b a∗b 的方案数求前缀和即可快速得到 c , d c,d c,d 的方案数
同理对于确定 a , i a,i a,i 来说用同样的方式计算 c ∗ d c * d c∗d 方案数的 后缀和 就可以快速得到 a , b a,b a,b 的方案数
当 前 a 的 方 案 种 数 = ( 当 前 魔 法 值 等 于 b 的 魔 法 物 品 总 量 ) ∗ ( 后 面 得 到 的 若 干 个 c 的 魔 法 物 品 总 量 ) ∗ ( 后 面 得 到 的 若 干 个 d 的 魔 法 物 品 总 量 ) 当前a的方案种数=(当前魔法值等于b的魔法物品总量)*(后面得到的若干个c 的魔法物品总量)*(后面得到的若干个d 的魔法物品总量) 当前a的方案种数=(当前魔法值等于b的魔法物品总量)∗(后面得到的若干个c的魔法物品总量)∗(后面得到的若干个d的魔法物品总量)
当 前 b 的 方 案 种 数 = ( 当 前 魔 法 值 等 于 a 的 魔 法 物 品 总 量 ) ∗ ( 后 面 得 到 的 若 干 个 c 的 魔 法 物 品 总 量 ) ∗ ( 后 面 得 到 的 若 干 个 d 的 魔 法 物 品 总 量 ) 当前b的方案种数=(当前魔法值等于a的魔法物品总量)*(后面得到的若干个c 的魔法物品总量)*(后面得到的若干个d 的魔法物品总量) 当前b的方案种数=(当前魔法值等于a的魔法物品总量)∗(后面得到的若干个c的魔法物品总量)∗(后面得到的若干个d的魔法物品总量)
这种做法的复杂度是 O ( n 2 ) O(n^2) O(n2) 但是这里的 n n n 其实是 n / 9 n / 9 n/9 所以完全不会超时
#include
using namespace std;
int a[15005], b[15005], c[15005], d[15005], w[15005], h[40005];
int n, m, x, y;
//abcd表示某个点作为abcd物品出现的次数
//w表示数轴上每个点出现的次数,h表示每个物品的魔法值
//n表示最大魔法值,m表示物品数量
int main(){
scanf("%d%d", &n, &m);
for(int i = 1; i <= m; i++){
scanf("%d", &h[i]);
w[h[i]]++;//把这些点标记在数轴上
}
for(int i = 1; i <= n / 9; i++){
//若数轴上有一个魔法阵:ABCD,其中有AB=2*CD,BC>6*CD
//所以只需枚举CD的长度就可以了
x = 1 + 9 * i;//x为AD最短长度
y = 0;
for(int j = 2 + 9 * i; j <= n; j++){
//因为数轴是从 1 开始的,所以从 1 + x 开始枚举
//枚举 D 点即 j ,则 C 点为 j - i , A 点为 j - x,B 点为 j - x + 2 * i
//CD 的个数取决于 AB 有多少组,所以我们用 y 表示 AB 的组数
y += w[j - x] * w[j - x + i + i];//y为AB的对数
//D 点是不定的。但是 D 点变化时,之前合格的 AB 两点仍然合格,所以要累加
d[j] += y * w[j - i];//有几组 AB,就有几个 C 点,就有几个 D 点
c[j - i] += y * w[j];//有几组 AB,就有几个 D 点,就有几个 C 点
}
//注意,魔法值可能重复,所以在加的时候,注意不要直接加。
//同理,枚举 CD 两点,确定 AB 的个数
x = 8 * i + 1;
y = 0;
for(int j = n - 9 * i - 1; j >= 1; j--){
y += w[j + x] * w[j + x + i];
a[j] += y * w[j + i + i];
b[j + i + i] += y * w[j];
}
}
for(int i = 1; i <= m; i++){
printf("%d %d %d %d\n",a[h[i]], b[h[i]], c[h[i]], d[h[i]]);
}
return 0;
}