E.有趣的数学题---斐波那契数列的最大公约数+矩阵快速幂

有趣的数学题

Time Limit 1000MS
Memory Limit 256MB

题目链接https://csustacm.fun/problem/1106

---

emmm，题目看起来很恐怖，实际上它确实有点。。。

碰到这种题目对于非数学选手来说只能默默地打表找规律：




…
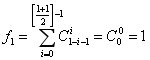
然后就会发现这TM不就是斐波那契数列嘛！f(n)=f(n-1)+f(n-2)。

如此一来f(n)的式子就算解决了。。。

接下来就是计算

而很显然，对于过大的f(n)我们无法保存它的值，那么对于取它们的最大公约数显然也不现实。也许有的人会说对f(n)取模再算最大公约数，显然这个想法是不对的，取模后的最大公约数不一定是它原本的最大公约数，再次取模后就会造成二次误差。。。。

里面的式子我们先不管，我们就算一算gcd(f(n),f(m))，找找规律：
gcd(f(1),f(2))=gcd(1,1)=1
而很显然，gcd(f(n),f(n+1))=1

简单证明：通过更相减损术可得，对于 gcd(a,a+x)=gcd(a,x)
那么 gcd(f(n),f(n+1))=gcd(f(n),f(n)+f(n-1))=gcd(f(n),f(n-1))
重复操作就可得gcd(f(n),f(n+1))=gcd(f(1),f(2))=1

那么对于任意的f(n)和f(m)呢？
gcd(f(4),f(8))=gcd(3,21)=3;
gcd(f(5),f(10))=gcd(5,55)=5;
gcd(f(12),f(18))=gcd(144,2584)=8;
gcd(f(10),f(15))=gcd(55,610)=5
…
实际上我们细心一点就会发现
gcd(f(4),f(8))=f(4)=3;
gcd(f(5),f(10))=f(5)=5;
gcd(f(12),f(18))=f(6)=8;
gcd(f(10),f(15))=f(5)=5;
…
然后我们不妨大胆假设：
gcd(f(n),f(m))=f(gcd(n,m))

那么基本这题就差不多结束了，只不过我们要把
f(n-1)* f(m)+f(m+1)* f(n)用f(t)来表示
那么不难算出t=n+m;
那么同样可以得出另一个式子为f(x+y)

那么最后的结果就是：

接下来就很简单了，学过矩阵快速幂的都知道怎么做了我就不多说了，AC代码之后有具体的证明。

以下是AC代码：

#include 
using namespace std;
#define ll long long
const int mod=1e9+7;
struct Mat
{
	ll m[5][5];
};
Mat mult(Mat a,Mat b){
	Mat mp;
	for (int i=1; i<=2; i++)
	 for (int j=1; j<=2; j++){
	 	mp.m[i][j]=0;
	 	for (int k=1; k<=2; k++){
	 		mp.m[i][j]=(mp.m[i][j]+(a.m[i][k]%mod)*(b.m[k][j])%mod)%mod;
		 }
	 }
	return mp;
}
Mat qick(Mat a,ll n){
	Mat unit;
	unit.m[1][1]=unit.m[2][2]=1;
	unit.m[1][2]=unit.m[2][1]=0;
	while (n){
		if (n&1) {
			unit=mult(unit,a);
		}
		n>>=1;
		a=mult(a,a);
	}
	return unit;
}
ll gcd(ll a,ll b){
	return b==0?a:gcd(b,a%b);
}
int main()
{
	ll n,m,x,y;
	cin>>n>>m>>x>>y;
	ll final=gcd(n+m,x+y);
	//cout<
	Mat ans;
	ans.m[1][1]=ans.m[1][2]=ans.m[2][1]=1;
	ans.m[2][2]=0;
	Mat sum=qick(ans,final-1);
	cout<<sum.m[1][1]<<endl;
	return 0;
}

蒟蒻如我只能对着这些证明喊会长6666了。。。