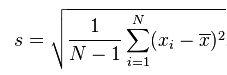机器学习之数据预处理方式（去均值、归一化、PCA降维）

目录

一、在介绍去均值和归一化之前，先介绍几个概念

1.1 平均值

1.2 方差、标准差

1.3 贝赛尔修正

1.4 平均值与标准差的适用范围及误用

1.5 为什么正态分布非常常见

二、常用数据预处理方法

2.1 去均值

2.2 .两种归一化的适用范围

2.3 PCA/白化

---

一、在介绍去均值和归一化之前，先介绍几个概念

1.1 平均值

平均值的概念很简单：所有数据之和除以数据点的个数，以此表示数据集的平均大小；其数学定义为 

以下面10个点的CPU使用率数据为例，其平均值为17.2。

14 31 16 19 26 14 14 14 11 13

 

---

1.2 方差、标准差

方差这一概念的目的是为了表示数据集中数据点的离散程度；其数学定义为： 
 
标准差与方差一样，表示的也是数据点的离散程度；其在数学上定义为方差的平方根： 

---

为什么使用标准差？

一个标准差 68%， 两个标准差 95%, 三个标准差 99%。

标准差定义是总体各单位标准值（ xi）与其平均数（μ）离差平方和的算术平均数的平方根。它反映组内个体间的离散程度。

所有数减去其平均值的平方和，所得结果除以该组数之个数（或个数减一，即变异数），再把所得值开根号，所得之数就是这组数据的标准差。

标准计算公式：

假设有一组数值X₁,X₂,X₃,......Xn（皆为实数），其平均值（算术平均值）为μ，公式如图1。

标准差也被称为标准偏差，或者实验标准差，公式为

一个较大的标准差，代表大部分数值和其平均值之间差异较大；一个较小的标准差，代表这些数值较接近平均值。

例如，A、B两组各有6位学生参加同一次语文测验，A组的分数为95、85、75、65、55、45，B组的分数为73、72、71、69、68、67。这两组的平均数都是70，但A组的标准差约为17.08分，B组的标准差约为2.16分，说明A组学生之间的差距要比B组学生之间的差距大得多。

一个标准差 68%， 两个标准差 95%, 三个标准差 99%。

与方差相比，使用标准差来表示数据点的离散程度有3个好处：

1. 表示离散程度的数字与样本数据点的数量级一致，更适合对数据样本形成感性认知。依然以上述10个点的CPU使用率数据为例，其方差约为41，而标准差则为6.4；两者相比较，标准差更适合人理解。
2. 表示离散程度的数字单位与样本数据的单位一致，更方便做后续的分析运算。
3. 在样本数据大致符合正态分布的情况下，标准差具有方便估算的特性：66.7%的数据点落在平均值前后1个标准差的范围内、95%的数据点落在平均值前后2个标准差的范围内，而99%的数据点将会落在平均值前后3个标准差的范围内。

---

1.3 贝赛尔修正

在上面的方差公式和标准差公式中，存在一个值为N的分母，其作用为将计算得到的累积偏差进行平均，从而消除数据集大小对计算数据离散程度所产生的影响。不过，使用N所计算得到的方差及标准差只能用来表示该数据集本身(population)的离散程度；如果数据集是某个更大的研究对象的样本(sample)，那么在计算该研究对象的离散程度时，就需要对上述方差公式和标准差公式进行贝塞尔修正，将N替换为N-1： 
经过贝塞尔修正后的方差公式：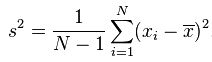 

经过贝塞尔修正后的标准差公式： 

公式的选择

是否使用贝塞尔修正，是由数据集的性质来决定的：如果只想计算数据集本身的离散程度(population)，那么就使用未经修正的公式；如果数据集是一个样本(sample)，而想要计算的则是样本所表达对象的离散程度，那么就使用贝塞尔修正后的公式。在特殊情况下，如果该数据集相较总体而言是一个极大的样本 (比如一分钟内采集了十万次的IO数据) — 在这种情况下，该样本数据集不可能错过任何的异常值(outlier)，此时可以使用未经修正的公式来计算总体数据的离散程度。

 

1.4 平均值与标准差的适用范围及误用

大多数统计学指标都有其适用范围，平均值、方差和标准差也不例外，其适用的数据集必须满足以下条件：

中部单峰：

1. 数据集只存在一个峰值。很简单，以假想的CPU使用率数据为例，如果50%的数据点位于20附近，另外50%的数据点位于80附近（两个峰），那么计算得到的平均值约为50，而标准差约为31；这两个计算结果完全无法描述数据点的特征，反而具有误导性。

2. 这个峰值必须大致位于数据集中部。还是以假想的CPU数据为例，如果80%的数据点位于20附近，剩下的20%数据随机分布于30~90之间，那么计算得到的平均值约为35，而标准差约为25；与之前一样，这两个计算结果不仅无法描述数据特征，反而会造成误导。

遗憾的是，在现实生活中，很多数据分布并不满足上述两个条件；因此，在使用平均值、方差和标准差的时候，必须谨慎小心。

如果数据集仅仅满足一个条件：单峰。那么，峰值在哪里？峰的宽带是多少？峰两边的数据对称性如何？有没有异常值(outlier)？为了回答这些问题，除了平均值、方差和标准差，需要更合适的工具和分析指标，而这，就是中位数、均方根、百分位数和四分差的意义所在。

1.5 为什么正态分布非常常见

整理内容来自这里→正态分布为什么常见

这里需要提到中心极限定理（central limit theorem）

在自然界与生产中，一些现象受到许多相互独立的随机因素的影响，如果每个因素所产生的影响都很微小时，总的影响可以看作是服从正态分布的。

可以看出，随着统计量个数的增加，它们和的平均值越来越符合正态分布。

正态分布只适合各种因素累加的情况，如果这些因素不是彼此独立的，会互相加强影响，那么就不是正态分布了。

如果各种因素对结果的影响不是相加，而是相乘，那么最终结果不是正态分布，而是对数正态分布（log normal distribution），即x的对数值log(x)满足正态分布。

也就是结果的对数值满足正态分布
相关参考：https://blog.csdn.net/zongzi13545329/article/details/84793959

二、常用数据预处理方法

2.1 去均值

各维度都减对应维度的均值，使得输入数据各个维度都中心化为0，进行去均值的原因是因为如果不去均值的话会容易拟合。   这是因为如果在神经网络中，特征值x比较大的时候，会导致W*x+b的结果也会很大，这样进行激活函数（如relu）输出时，会导致对应位置数值变化量太小，进行反向传播时因为要使用这里的梯度进行计算，所以会导致梯度消散问题，导致参数改变量很小，也就会易于拟合，效果不好。

右图为去均值之后的效果。

                 

2.2 .两种归一化的适用范围

一种是最值归一化，比如把最大值归一化成1，最小值归一化成-1；或把最大值归一化成1，最小值归一化成0。适用于本来就分布在有限范围内的数据.另一种是均值方差归一化，一般是把均值归一化成0，方差归一化成1。适用于分布没有明显边界的情况。

                           

进行归一化的原因是把各个特征的尺度控制在相同的范围内，这样可以便于找到最优解，不进行归一化时如左图，进行归一化后如右图，可发现能提高收敛效率，省事多了。

    

2.3 PCA/白化

1.PCA是指通过抛弃携带信息量较少的维度，保留主要的特征信息来对数据进行降维处理，思路上是使用少数几个有代表性、互不相关的特征来代替原先的大量的、存在一定相关性的特征，从而加速机器学习进程。（降维技术可单独讲）      

 PCA可用于特征提取，数据压缩，去噪声，降维等操作。      

2.白化的目的是去掉数据之间的相关联度和令方差均一化，由于图像中相邻像素之间具有很强的相关性，所以用于训练时很多输入是冗余的。这时候去相关的操作就可以采用白化操作，从而使得:                    

       1.减少特征之间的相关性                    

       2.特征具有相同的方差（协方差阵为1）      

3.举个白化的例子，如对于两个特征的关联分布如左图，可以看出特征组合点存在线性关系，此时我们进行白化后（特征向量的投影）可以变成右图的形式，无关联性。    

而且白化因为进行了方差均一化，所以还可以提升训练速度。      

相关参考：

https://blog.csdn.net/maqunfi/article/details/82252480 

https://www.cnblogs.com/quietwalk/p/8243536.html