LeetCode 198 & 213 & 337.打家劫舍问题（动态规划算法的理解）

前几天在LeetCode的时候碰到几道打家劫舍问题，觉得挺有意思，在这里跟大家一起学习一下。首先我们来看第一题：

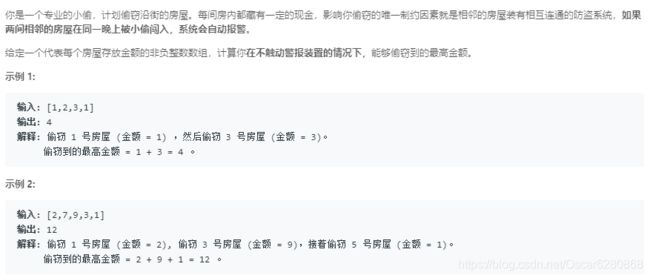
相信有的朋友拿到这道题想法是和我一样的，那就是暴力解法，我用两层for循环来遍历每一个房间，后来发现这样其实太麻烦了，并且还无法考虑到一些特定的情况，所以提交了很多次都没有提交过。后来看到评论里有朋友提示使用动态规划，于是我试着用递归的方法去解决这样的问题，下面详见代码：

class Solution {
    public int rob(int[] nums) {
        if (nums.length == 0){
            return 0;
        }

        if (nums.length == 1){
            return nums[0];
        }

        if (nums.length == 2){
            return Math.max(nums[0], nums[1]);
        }

        int[] result = new int[nums.length];   
        result[0] = nums[0];
        result[1] = Math.max(nums[0], nums[1]);

        for(int index=2; index < result.length; index++){
            result[index] = Math.max(nums[index] + result[index-2], result[index -1]);
        }

        return result[nums.length -1];
    }
}

首先我们考虑数组长度小于2的一些情况，这些情况的代码都是比较容易理解的，然后后面就是数组大于2的情况了，这就像斐波那契数列一样，我们首先定义一个数组初始化数列的前两位：

int[] result = new int[nums.length];   
result[0] = nums[0];
result[1] = Math.max(nums[0], nums[1]);

这个数组result表示在第i个房间可以偷得的最高金额，因为不能够偷连续的两个房间，所以我们在递归的时候，可以表示成：

for(int index=2; index < result.length; index++){
	 result[index] = Math.max(nums[index] + result[index-2], result[index -1]);
}

这样的动态规划，一层层地递归，就可以满足我们的所有情况，也不用我们考虑种种我们考虑不到的情况了。这样一来，看似复杂的问题，递归拆分之后就变得简单了。接着这道题又有一道这道题的升级版：

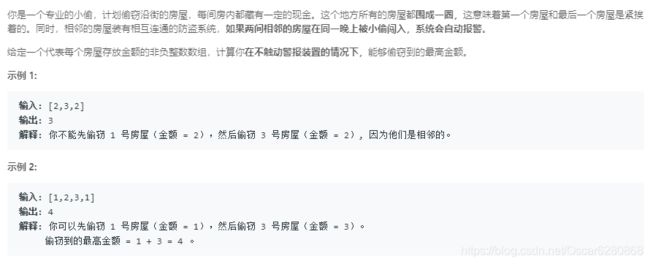
这道题的思路其实和上一题大同小异，只是把首位相连，我们可以将这道题拆分一下，既然首尾相连，我们就把这个数组拆分成nums[0]-nums[n-1]和nums[1]-nums[n]两个部分，然后按照上一题的方法分别计算一下两个数组的最大金额，然后取这两个值中较大的那个值就是我们能在这个环形的小区所能够偷得最大值，最开始拿到这个题目其实看似无从下手，但是如果能想到吧环形的数组拆分成两个数组，就可以将这个问题拆分成上一题的问题，我们来看看代码吧：

class Solution {
    public int rob(int[] nums) {
        if(nums.length == 0){
            return 0;
        }
        if(nums.length == 1){
            return nums[0];
        }
        if(nums.length == 2){
            return Math.max(nums[0], nums[1]);
        }
        int[] result1 = new int[nums.length - 1];
        int[] result2 = new int[nums.length - 1];
        
        result1[0] = nums[0];
        result1[1] = Math.max(nums[0], nums[1]);
        
        result2[0] = nums[1];
        result2[1] = Math.max(nums[1], nums[2]);
        
        for(int i = 2; i < result1.length; i++){
            result1[i] = Math.max(nums[i] + result1[i - 2], result1[i - 1]);
        }
        
        for(int j = 2; j < result2.length; j++){
            result2[j] = Math.max(nums[j + 1] + result2[j - 2], result2[j - 1]);
        }
        return Math.max(result1[nums.length - 2], result2[nums.length - 2]);
    }
}

这里需要注意的是，因为我们将数组进行了拆分，所以在数组里面的参数不要弄错了，这题的思想和上一题其实是一样的，关键是能否考虑到将环形的小区拆分成两个线性的小区。 现在还有个打家劫舍的升级题目，就是将我们的数组换成了二叉树：

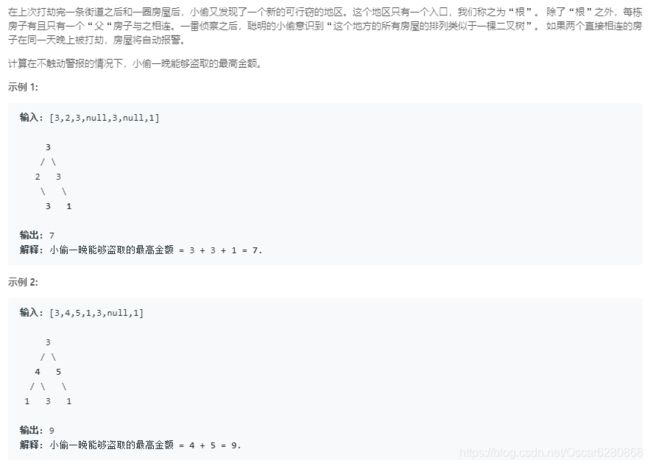
在拿到这个二叉树的题目的时候，发现毫无思路可言，但是想到动态规划，我们去找一下这个二叉树小区的规律，我们可以发现，在二叉树中，如果偷了一个节点，那么和它相邻的节点都不可以偷了，也就是说，偷了二叉树中的某一层的话，那么和这一层相邻的层都不可以偷了，我们将房间的概念换成二叉树层的概念就方便理解了，我们同样可以用动态规划的思想：

class Solution {
    public int rob(TreeNode root) {
        if(root == null)
            return 0;
        int s0 = 0;
        int s1 = root.val;        
        s0 = rob(root.left) + rob(root.right);     
        if(root.left != null)
            s1 += rob(root.left.left) + rob(root.left.right);
        if(root.right != null)
            s1 += rob(root.right.left) + rob(root.right.right);
        return Math.max(s0,s1);
    }
}

s1表示偷根节点所在的那一层和不和它相邻的层，s0表示偷和根节点相邻的那一层，然后我们用动态规划的思想就可以解决这个问题了。其实这一类问题的解法并不难，但是很难想到动态规划如何用在这类似的题目当中，希望这篇博文能够让大家对动态规划算法的理解有所提升，谢谢。