CORDIC算法详解(四)-CORDIC 算法之双曲系统及其数学应用

CORDIC算法详解（四）- CORDIC 算法之双曲系统及其数学应用

  网上有很多类似的介绍，但是本文会结合实例进行介绍，尽量以最简单的语言进行解析。
  CORDIC ( Coordinate Rotation Digital Computer ) 是坐标旋转数字计算机算法的简称，
由 Vloder• 于 1959 年在设计美国航空导航控制系统的过程中首先提出[1], 主要用于解决导航系统中三角函数、 反三角函数和开方等运算的实时计算问题。 1971 年， Walther 将圆周系统、 线性系统和双曲系统统一到一个 CORDIC 迭代方程里 ， 从而提出了一种统一的CORDIC 算法形式[2]。
  CORDIC 算法应用广泛， 如离散傅里叶变换 、 离散余弦变换、 离散 Hartley 变换、Chirp-Z 变换、 各种滤波以及矩阵的奇异值分解中都可应用 CORDIC 算法。 从广义上讲，CORDIC 算法提供了一种数学计算的逼近方法。 由于它最终可分解为一系列的加减和移位操作， 故非常适合硬件实现。 例如， 在工程领域可采用 CORDIC 算法实现直接数字频率合成器。 本节在阐述 CORDIC 算法三种旋转模式的基础上， 介绍了利用 CORDIC 算法计算三角函数、 反三角函数和复数求模等相关理论。 以此为依据， 阐述了基于 FPGA 的 CORDIC 算法的设计与实现及其工程应用。

---

整个系列分别从圆周系统、 线性系统和双曲系统及硬件实现进行分析，如下：

CORDIC算法详解（一）- CORDIC 算法之圆周系统之旋转模式（ Rotation Mode )
CORDIC算法详解（二）- CORDIC 算法之圆周系统之向量模式（Vectoring Mode）
CORDIC算法详解（三）- CORDIC 算法之线性系统及其数学应用
CORDIC算法详解（四）- CORDIC 算法之双曲系统及其数学应用
CORDIC算法详解（五）- 统一的 CORDIC 算法形式
CORDIC算法详解（六）- CORDIC 算法的硬件实现
其中第五篇及第六篇后会放出相关参考资料及源码。

---

4 CORDIC 算法之双曲系统及其数学应用

4.1 CORDIC 算法之双曲系统

  如图 3.87 所示， 在等轴双曲线的右半支上， 向量 OP与 X 正半轴夹角为 α, 故 P 点 坐标可表示为:


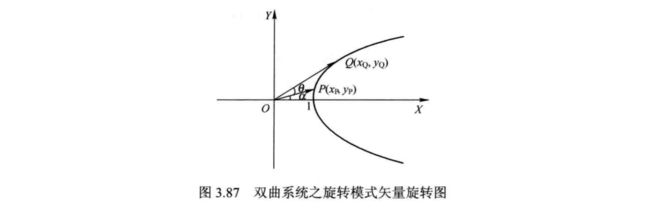
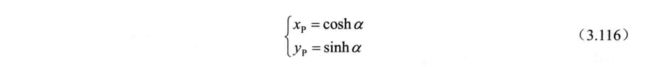
  将向量 OP 逆 时 针 旋 转 θ 角 至 向 量 OQ，此 时OQ 与 X 轴 正 半 轴 夹 角 为 a +θ 故 Q 点 坐 标可表示为:

  这里定义 θ 为目标旋转角度。 根据双曲函数公式可将式 (3.117) 展开为

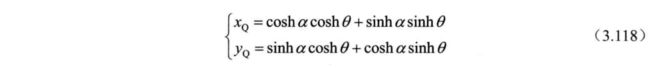
  将式 (3.116) 代入式 (3.118) 可得:

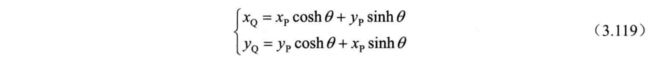
  提取 coshθ , 式 (3.119) 可重写为:

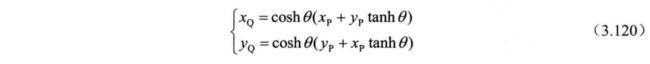
  类似于圆周系统下的分析方法， 将θ 分解为一系列的θ_i的线性组合， 其中:

式中d_i∈{-1, +1}。由于tanh^-12^-i=∞，故 i 从 1 开始。 类似地将旋转转换伪旋转下的微旋转，可得旋转模式和向量模式下的迭代公式， 如图 3.88 所示。

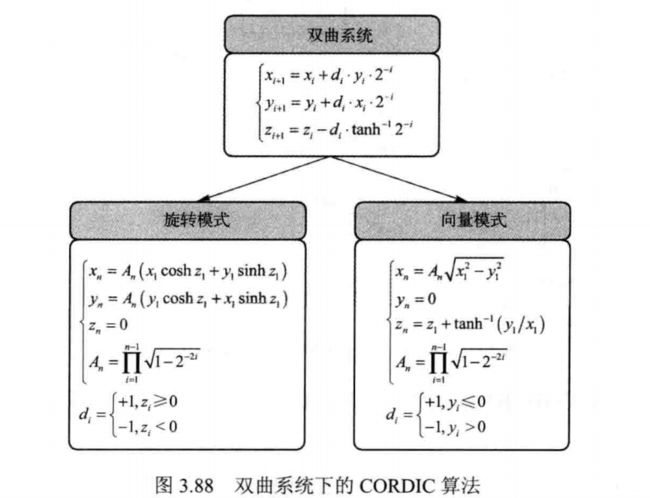
  与圆周系统和线性系统有所不同， 双曲系统的迭代较为复杂。 其迭代过程要求当迭代顺序号为 4、 13、 40 等满足 i = 3k+ 1 时， 该次迭代必须重复， 才能保证收敛， 从而迭代过程变i = 1,2,3,4,4,5,… 。 根据迭代次数可确定图 3.88 中A_n≈0.82815936（n–>∞），故模长补偿因子为K≈1.20749706。同时还可确定旋转角度的总和为：

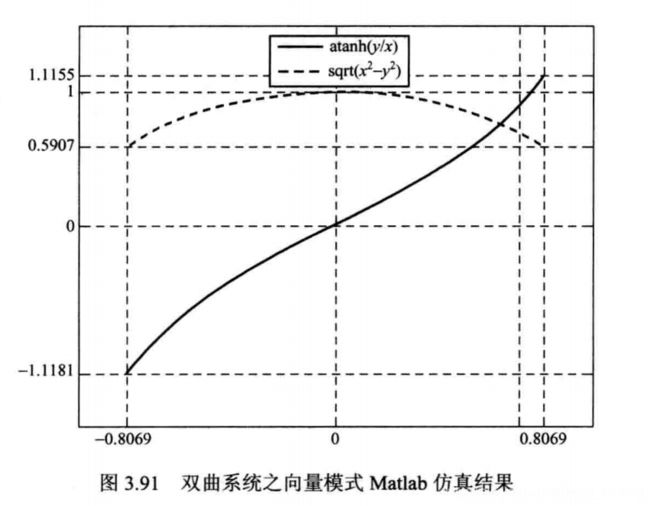
  这就限定了在旋转模式下，初始化z_i的取值范围为[-1.1181,+1.1181]，在向量模式下 （y₁/x₁）的取值范围为[-0.8069,+0.8069] 。

4.2 CORDIC 算法之双曲系统数学应用

  利用双曲系统可求取一系列超越函数。 在旋转模式下， 可求取双曲正弦函数和双曲余弦函数， 进而可求取 e 指 数， 如 图 3 . 8 9 所 示。 据 此， 可 得 MATLAB下的仿真结果如3.90 所示。

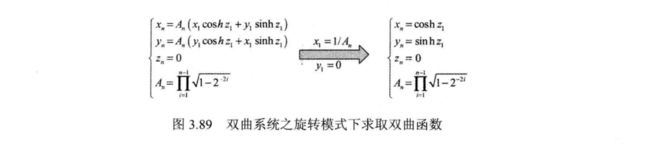
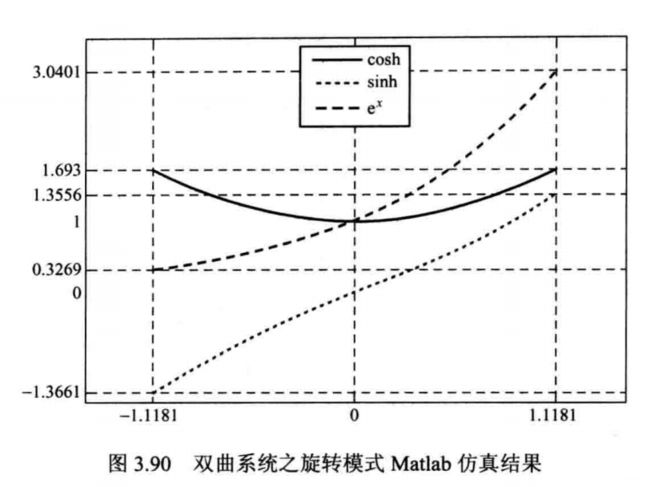
  在向量模式下， CORDIC 算法可实现反双曲正切函数的计算， MATLAB仿真结果如 3.91所示。

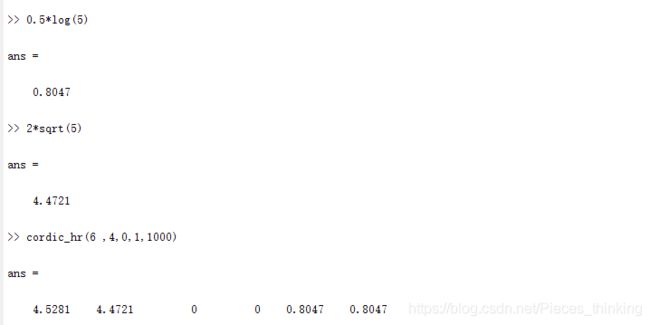
  除了可进行反双曲正切函数的计算外， 还可进行对数运算以及开方运算， 如 3.92 所示。

  由于向量模式下， 限定了（y₁/x₁）的取值范围为[-0.8069,+0.8069] , 故在对数运算和开方运算时， 图 3.92 中的α 需满足

从而可确定α∈[0.1069，9.3573]。

4.3 CORDIC 算法之双曲系统MATLAB代码

  CORDIC 双曲系统算法模型如 MATLAB 代码 如下， 该函数调用了函数 cordic_hr_it，具体如下：

MATLAB 代码 3-7 function: cordic_hr

% /*
% * @Author: ZLK
% * @Date:   2018-10-31 10:00:17
% * @Last Modified by:   ZLK
% * @Last Modified time: 2018-10-31 13:50:05
% */
function a = cordic_hr(x1,y1,z1,mode,it)
% mode: 0 rotation mode, 1 vectoring mode.
% it: iteration number.
if it<4
	error('Iterations must be greater than 3');
end
if mode==0
	if abs(z1)>1.1181
		error('In rotation mode abs(zl)<1.1181');
	end
else
	if abs(y1/x1)>0.8069
		error('In vectoring mode abs(yl/xl)<0.8069');
	end
end
myit = cordic_hr_it(it);
len_myit = length(myit);
x = zeros(len_myit+1,1);
y = zeros(len_myit+1,1);
z = zeros(len_myit+1,1);
x(1) = x1;
y(1) = y1;
z(1)= z1;
di = 0;
for k=1:len_myit
	if mode==0
		di = sign(z(k));
	else
		di = sign(-y(k));
	end
	x(k+1) = x(k)+ y(k)*di*2^(-myit(k));
	y(k+1) = y(k)+ x(k)*di*2^(-myit(k));
	z(k+1) = z(k)- di*atanh(2^(-myit(k)));
end

kn = 1/prod(sqrt(1-2.^(-2*myit)));
xn = kn*x(it+1);
yn = kn*y(it+1);
zn = z(it+1);

if mode==0
	xt = x1*cosh(z1)+y1*sinh(z1);
	yt = y1*cosh(z1)+x1*sinh(z1);
	zt = 0;
else
	xt = sqrt(x1^2-y1^2);
	yt = 0;
	zt = z1+atanh(y1/x1);
end

a = [xn, xt,yn,yt,zn,zt];

MATLAB 代码 3-8 function: cordic_hr_it

% /*
% * @Author: ZLK
% * @Date:   2018-10-31 13:50:22
% * @Last Modified by:   ZLK
% * @Last Modified time: 2018-10-31 13:52:57
% */
function it = cordic_hr_it(kmax)
% return cordic hybolic system iteration index
it = zeros(kmax,1);
it(1) = 1;
k = 1;
repeat_value = 4;
while k+1<=kmax
	it(k+1) = it(k)+ 1;
	if it(k+1)==repeat_value && k+2<=kmax
		it(k+2)= it(k+1);
		repeat_value = 3*repeat_value+1;
		k = k+2;
	else
		k = k+1;
	end
end

  结果

  相关参数转换如下：

• x₁=1；（本程序中，表示x₁cosh/x₁sinh，因为程序中已经进行了相关的计算）

• y₁ = 0；
• z₁=π/4 ；（cosh(z₁=π/4)/sinh(z₁=π/4)）
• 经过100次迭代计算后，得到的xn 和yn分别为coshθ和sinhθ。

• α=5

• x₁=6；（本程序中，表示x₁cosh/x₁sinh，因为程序中已经进行了相关的计算）

• y₁ = 4；

• z₁=0 ；（cosh(z₁=π/4)/sinh(z₁=π/4)）

• 经过1000次迭代计算后，得到的xn 和yn分别为2α^0.5和0.5ln(α)。
  
    其中开方操作，还有点误差，还在查找原因。