LR电路的暂态过程
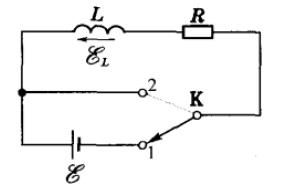
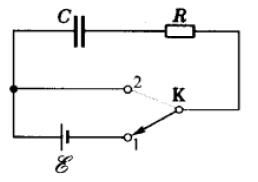
由电感和电阻组成的电路称为LR电路，如图1所示。
图1 LR电路
如图1，当开关拨向1时，电路中出现自感电动势，
\begin{equation*} \mathcal{E}_L=-L\frac{\mathrm di}{\mathrm dt} \end{equation*}
根据欧姆定律，有
\begin{equation*} \mathcal{E}+\mathcal{E}_L=\mathcal{E}-L\frac{\mathrm di}{\mathrm dt}=iR \end{equation*}
这是一个微分方程，其解为
\begin{equation*} i=\frac{\mathcal{E}}{R}+K_1e^{-\frac{R}{L}t} \end{equation*}
根据初始条件，\(t=0\)时，\(i=0\)，因而有
\begin{equation*} i=\frac{\mathcal{E}}{R}\left (1-e^{-\frac{R}{L}t}\right )=I_0\left (1-e^{-t/\tau}\right ) \end{equation*}
即接通电路后，电流随时间而增长，其最大值\(I_0=\frac{\mathcal{E}}{R}\)就是电流达到稳定值时的值。其中\(\tau=L/R\)为LR电路的时间常量。
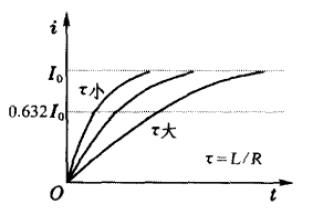
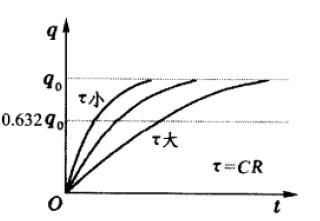
不同\(\tau\)下，LR电路接通电流随时间的变化如图2所示。
图2 LR电路接通电流随时间的变化
从数学上看，接通电路后，要经历无限长的时间，电流才能达到稳定值。实际上，
\begin{equation*} i(\tau)=I_0\left (1-e^{-1}\right )=0.63I_0 \end{equation*}
\begin{equation*} i(5\tau)=I_0\left (1-e^{-5}\right )=0.99I_0 \end{equation*}
所以，只要\(t\gg \tau\)，就可认为电流达到稳定值。所以，LR电路的时间常量\(\tau=L/R\)可以表征暂态过程持续时间长短。\(L\)越大，\(R越小\)，则\(\tau\)越大，电流增长得越慢，暂态过程越持久。
将图1中开关从1拨向2，根据欧姆定律，电流\(i\)满足如下方程
\begin{equation*} -L\frac{\mathrm di}{\mathrm dt}=iR \end{equation*}
并有初始条件，\(t=0\)时，\(i=I_0=\frac{\mathcal{E}}{R}\)，因而有
\begin{equation*} i=\frac{\mathcal{E}}{R}e^{-\frac{R}{L}t}=I_0 e^{-t/\tau} \end{equation*}
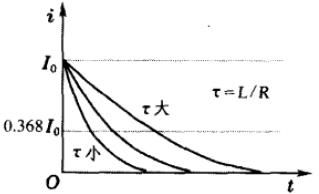
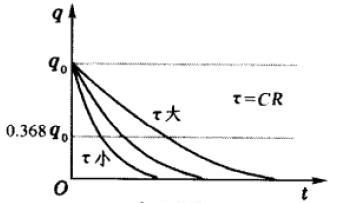
即断开电源后，电流不是立即变为0，而是按指数衰减，衰减快慢程度用LR电路的时间常量\(\tau=L/R\)来表征。电流随时间的变化如图3所示。
图3 LR电路断开，电流随时间的变化
课堂思考：
1 LR电路中，磁能随时间如何变化？
2 图1中，开关接1时，线圈和电阻两端，哪边电势高？
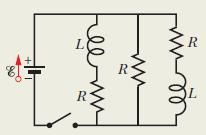
3 如下图所示电路，开关闭合瞬间，电路中电流为多少？很长时间后，电路中电流为多少？
课堂思考3 图
RC电路暂态过程
RC电路暂态过程就是电容器的充放电过程。
图4 RC电路
图4所示电路中，将开关接到位置1，电容器充电，电源电动势为电容器两极板电压与电阻R上的电势降落之和，即
\begin{equation*} \mathcal{E}=\frac{q}{c}+iR=\frac{q}{c}+\frac{\mathrm dq}{\mathrm dt}R \end{equation*}
其中\(i=\frac{\mathrm dq}{\mathrm dt}\)为电路中的瞬时电流。上式解之得，
\begin{equation*} q=C\mathcal{E}\left (1-e^{-\frac{1}{RC}t}\right )=C\mathcal{E}\left (1-e^{-t/\tau}\right ) \end{equation*}
开关接位置2，电容器放电，有
\begin{equation*} 0=\frac{q}{c}+iR=\frac{q}{c}+\frac{\mathrm dq}{\mathrm dt}R \end{equation*}
上式解之得，
\begin{equation*} q=C\mathcal{E}e^{-\frac{1}{RC}t}=C\mathcal{E}e^{-t/\tau} \end{equation*}
上式中\(\tau=RC\)为RC电路的时间常量，表示充放电过程的快慢。充放电过程中电容器电量\(q\)随时间变化的曲线如图5、6所示。
图5 RC电路充电过程
图6 RC电路放电过程
课堂思考：
1 RC电路中，电流随时间如何变化？
2 RC电路中，电能随时间如何变化？
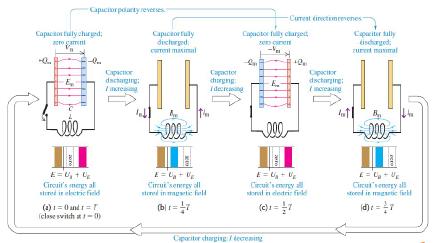
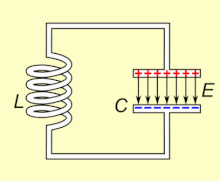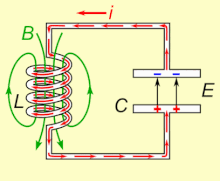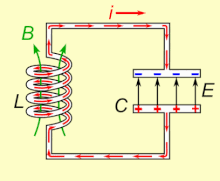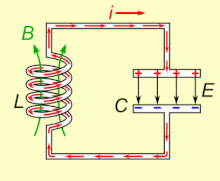
LC电路的暂态过程
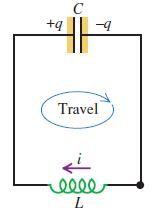
图7为LC电路。
图7 LC电路
电路满足方程
\begin{equation*} -L\frac{\mathrm di}{\mathrm dt}=\frac{q}{c} \end{equation*}
由于\(\frac{\mathrm di}{\mathrm dt}=\frac{\mathrm d^2q}{ dt^2}\)，于是上式可化为
\begin{equation*} \frac{\mathrm d^2q}{ dt^2}+\frac{1}{LC}q=0 \end{equation*}
这个方程与简谐振子的方程\(\frac{\mathrm d^2x}{ dt^2}+\frac{k}{m}x=0\)是一样的，所以方程的解也是类似的，
\begin{equation*} q=q_0\cos(\omega t+\phi) \end{equation*}
其中\(\omega=\frac{1}{\sqrt{LC}}\)，对于弹簧谐振子\(\omega=\sqrt{k/m}\)。
LC电路中的瞬时电流
\begin{equation*} i=\frac{\mathrm dq}{\mathrm dt}=-\omega q_0\sin(\omega t+\phi) \end{equation*}
相当于谐振子的质点速度。
LC电路中能量，磁能为\(\frac{1}{2}Li^2\)，相当于谐振子的质点的动能\(\frac{1}{2}mv^2\)，电能为\(\frac{q^2}{2C}\)，相当于谐振子的弹簧势能\(\frac{1}{2}kx^2\)。LC电路总能量为
\begin{equation*} \frac{1}{2}Li^2+\frac{q^2}{2C}=\frac{q_0^2}{2C} \end{equation*}
LC振荡电路中的能量转化如图8所示。
图8 LC振荡电路中的能量转化
图9 LC振荡电路中的能量转化动画
LCR 电路暂态过程
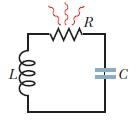
LCR电路如图10所示
图10 LCR电路
电量满足的方程
\begin{equation*} -L\frac{\mathrm di}{\mathrm dt}=iR+\frac{q}{C} \end{equation*}
即
\begin{equation*} L\frac{\mathrm d^2q}{\mathrm dt^2}+R\frac{\mathrm dq}{\mathrm dt}+\frac{q}{C}=0 \end{equation*}
这正是阻尼振动方程。
作业
习题 5-32