（leetcode：选择不相邻元素，求和最大问题）：打家劫舍（DP：198/213/337）

题型：从数组中选择不相邻元素，求和最大

（1）对于数组中的每个元素，都存在两种可能性：（1）选择（2）不选择，所以对于这类问题，暴力方法（递归思路）的时间复杂度为：O(2^n)；

（2）递归思路中往往会包含大量的重复计算，从时间角度出发，我们一般都会使用动态规划的方法来解决这类问题；而动态规划的核心思想就是：使用变量或者数组来记录重复出现的部分，这样会大大减少计算量，节省时间。

（3）在使用动态规划的方法解决这类问题时，一般过程是：

1. 最好先使用暴力分析的方法，按照题意将原题中给出的案例推导出来，然后从中总结规律，便于分析出状态转移方程
2. 定义DP状态，保存中间变量
3. 写出状态转移方程

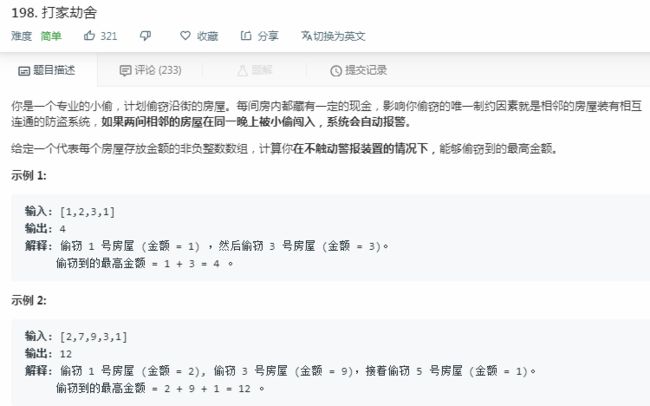
打家劫舍（leetcode 198）

 

分析：

（1）对于每个数组元素，都有两种选择：选与不选

（2）DP状态：opt[i] 表示：偷到第 i 间房屋时，小偷可以偷到的最大金额

（3）分析状态转移：

选： 　opt[i] = opt[i-2] + nums[i]

不选： opt[i] = opt[i-1]

则，opt[i] = max( opt[i-2] + nums[i],  opt[i-1])

 

python代码实现：

 1 class Solution:
 2     def rob(self, nums: List[int]) -> int:
 3         n = len(nums)
 4         if n == 0: return 0
 5         elif n < 2: return max(nums)
 6         else:
 7             opt = [0 for i in range(n)]
 8             
 9             opt[0] = nums[0]
10             opt[1] = max(nums[0], nums[1])
11             
12             for i in range(2, n):
13                 opt[i] = max(opt[i-1], opt[i-2]+nums[i])
14                 
15             return opt[-1]

View Code

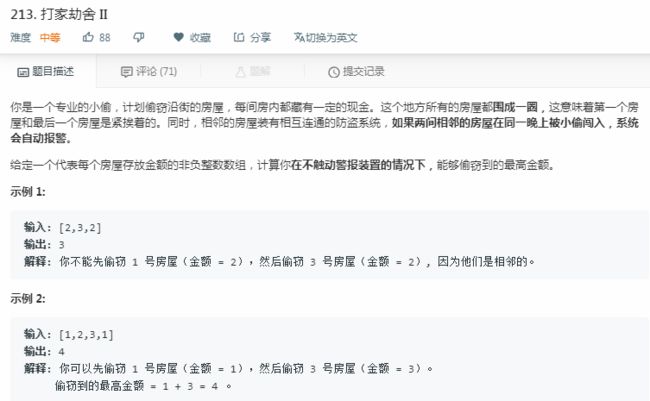
打家劫舍（leetcode：213）

 

分析：

（1）213与198相比，不同之处：198是首尾不相连的数组，213是首尾相连成环的数组；

（2）在开始做这个题的时候，很容易陷入一个误区：首尾相连成环，就必须得从环的角度出发来解决这个问题，这往往需要考虑很多的边界问题，而且很容易解出来。在这个时候，我们不防转换一下角度，联想一下之前做过的类似题目的思路（198），找一下可以借鉴的部分。

（3）环：首尾相连，每个位置的元素等同，不分初始位置和结束位置，但是环可以拆成首尾不相连的数组形式（198题）；

（4）要求是：选择的元素不相邻，所以，现在分为两种情况：1. 选择第一个位置的房屋金钱（不能选择最后一个位置的房屋金钱） 2. 选择最后一个位置的房屋金钱（不能选择第一个位置的房屋金钱），从这个角度就可以将环分成两个首尾不相连的数组形式，再使用198的思路进行求解；

python 代码实现：

 1 class Solution:
 2     def rob(self, nums: List[int]) -> int:
 3         n = len(nums)
 4         if n == 0: return 0
 5         elif n <= 3: return max(nums)
 6         else:
 7             nums_1 = [nums[i] for i in range(n-1)]
 8             nums_2 = [nums[i] for i in range(1, n)]
 9             
10             opt1 = [0 for i in range(n)]
11             opt2 = [0 for i in range(n)]
12             
13             opt1[0], opt2[0] = nums_1[0], nums_2[0]
14             opt1[1], opt2[1] = max(nums_1[0], nums_1[1]), max(nums_2[0],nums_2[1])
15             for i in range(2, n-1):
16                 opt1[i] = max(opt1[i-1], opt1[i-2]+nums_1[i])
17                 opt2[i] = max(opt2[i-1], opt2[i-2]+nums_2[i])
18             
19             return max(max(opt1), max(opt2))

View Code

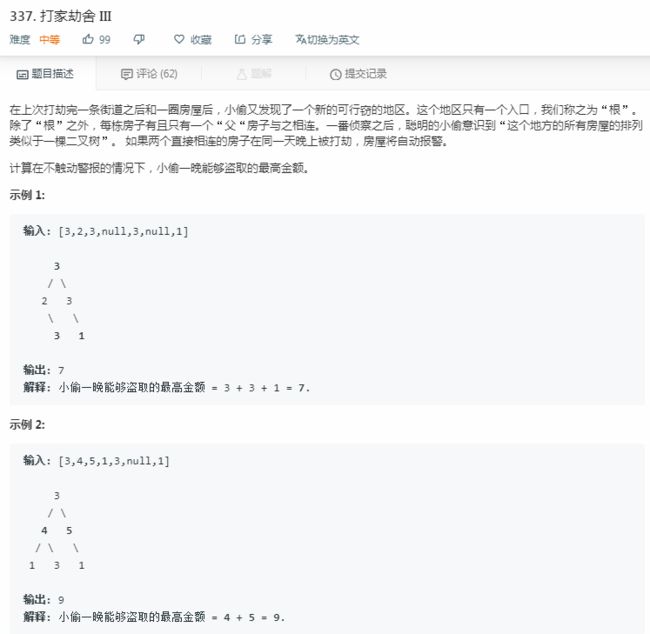
 打家劫舍（leecode：337）

分析：

（1）337是二叉树形式的数组，条件仍然是：选择的元素不相邻；

（2）从根节点出发，（选择的元素不相邻）其实是：不能同时选择父节点和子结点上的元素，但是可以选择兄弟节点，可以选择爷孙节点；

 

（数据结构中的树模型还没复习到，等复习完树模型之后再回来整理这个题的代码~~）

 

转载于:https://www.cnblogs.com/xdliyin/p/10779134.html