力扣——62.不同路径(中等难度)——如何学以致用

一、算法目录合集

1.地址

   算法目录合集

2.说明

  该地址指向所有由本人自己所经历的算法习题(也有可能仅仅是一个入门的案例或者是经典案例)，仅仅为我做过而且比较有意思的，也许还会有一些我自己想出来的，出于兴趣写在这里,具体格式我会在下面列明，总目录也会在这里出现，方便查阅以及自己进行复习回顾。

二、题目说明

1.题干

  一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。
  机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。
  问总共有多少条不同的路径？

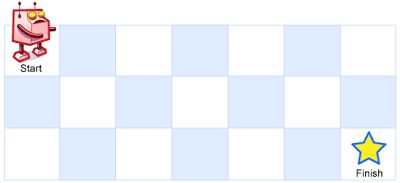
  例如，上图是一个7 x 3 的网格。有多少可能的路径？

示例1:
输入: m = 3, n = 2
输出: 3
解释:
从左上角开始，总共有 3 条路径可以到达右下角。

1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右

示例2:
输入: m = 7, n = 3
输出: 28

2.原地址

  62.不同路径

三、实现步骤

1.思路分析

  对于本题，其实了解过杨辉三角的人都很熟悉，这是一道典型的杨辉三角问题的变形。就像下题：

  解决方法就是按照杨辉三角的普遍规律：按照杨辉三角详解里面的推导方法来进行推导，或者直接采用二项式定理，推出所求的组合数。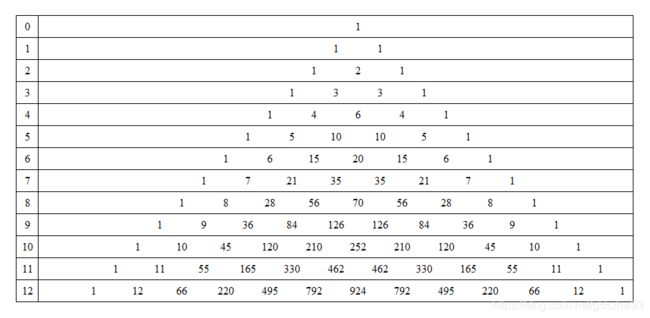
  下面我主要说一下怎么由简单例子找到规律，实现组合的问题的。

1.1.分析问题

  既然已经知道这是杨辉三角了，那么所求位置必然是类似于杨辉三角的组合数：$C_x^y$,下面我们要做的就是找到$x$是什么，$y$是什么。

1.2.转化问题

  我们先随便找几个例子：输入值为m=4，n=1的时候，对照杨辉三角的图，所得结果为4，应该为$C_3^3$，我们就猜测也许是$x=m+n-2$，$y=n+2$,然后我们再随便找一个，比如输入值为m=6，n=4的时候，，所得结果为56，应该为$C_8^5$，我们发现推测的$x=m+n-2$是正确的，可是$y=n+2$明显是不对的，那么怎么对应当m=4，n=1的时候y=3，m=6，n=4的时候，y=5呢？不难看出，y其实就是m-1，那么对不对呢，可以再随便找一个数验证一下，是正确的。

1.3.具体步骤

① 特殊情况分析

  在这里一般第一行是特殊的，是需要进行特殊值分析的，而在我们的代码中，完全可以把特殊值放进规则中进行讨论，所以也就不必单独拿出来了。
  但是有必要说明的是，后面我们做的递推是从每行的第一个数推到目标数的，所以尽量越少越好，因此我们运用$C_n^m=C_n^{n-m}$这一数学规律来进行简化，当目标值大的时候，我们就选取n-m，当目标值小的时候我们就用它自己：

long piles = m + n - 2;
long index = m - 1;
long min = Math.min(index, (piles - index));

  min就是我们要采用的索引位置。

② 常规分析

  既然推测出了答案就是$C_{m+n-2}^{m-1}$，那么只需要根据：
$$k=\frac{C_n^{r+1}}{C_n^r}=\frac{(n-r)}{(r+1)}$$
就可以做出递推公式了

long member = 1;
for (int i = 0; i < min; i++) {
     
	member = member * (piles - i) / (i + 1);
}

2.代码实现

2.1 方法代码

class Solution62 {
     
    public int uniquePaths(int m, int n) {
     
        long piles = m + n - 2;
        long index = m - 1;
        long min = Math.min(index, (piles - index));
        long member = 1;
        for (int i = 0; i < min; i++) {
     
            member = member * (piles - i) / (i + 1);
        }

        return (int) member;
    }
}

2.2 测试部分代码

这里随便定义一个随便看看就好了

public class Test62Middle {
     
    public static void main(String[] args) {
     
        Solution62 s = new Solution62();
        System.out.println(s.uniquePaths(51, 9));
    }
}

2.3 耗用资源情况

四、官方题解（官方未出，找几个不错的思路）

1.原地址

力扣官方答疑戳这里

2.方法一——动态规划

思路分析

思路
我们令 dp[i][j] 是到达 i, j 最多路径
动态方程：dp[i][j] = dp[i-1][j] + dp[i][j-1]
注意，对于第一行 dp[0][j]，或者第一列 dp[i][0]，由于都是在边界，所以只能为 1
优化：因为我们每次只需要 dp[i-1][j],dp[i][j-1]，所以我们只要记录这两个数。

代码实现

class Solution {
     
    public int uniquePaths(int m, int n) {
     
        int[] cur = new int[n];
        Arrays.fill(cur,1);
        for (int i = 1; i < m;i++){
     
            for (int j = 1; j < n; j++){
     
                cur[j] += cur[j-1] ;
            }
        }
        return cur[n-1];
    }
}

复杂度

• 时间复杂度：
    O(m*n)。
• 空间复杂度：
    O( n)。