多元回归与相关------（一）多元回归

一元回归：依变数Y对一个自变数X的回归。

多元回归或复回归（multiple regression）:依变数依两个或两个以上自变数的回归。

主要内容：

（1）确定各个自变数对依变数的单独效应和综合效应，建立由各个自变数描述和预测依变数反应量的多元回归方程。

（2）对上述综合效应和单独效用的显著性进行测验，并在大量自变数中选择仅对依变数有显著效用的自变数，建立最优多元回归方程

（3）评定各个自变数对依变数的相对重要性，以便研究者抓住关键，能动地调节依变数的响应量。

一、多元回归方程

（1）多元回归线性模型和多元回归方程式

依变数同时受到m个自变数X1，X2，...,Xm的影响，且这m个自变数皆与Y成线性关系，这m+1个变数的关系就形成m元线性回归：

线性模型：     其中， 

则一个m元线性回归的样本观察值组为：

误差项反映了除X1，X2，...,Xm与y的线性关系之外的随机因素对y的影响，是不能由X1，X2，...,Xm与y之间的线性关系所解释的变异性。

误差项  有三个基本假定：

（1）误差项  是一个期望值为0的随机变量，。意味着对于给定 X1，X2，...,Xm的值，y的期望值

（2）对于自变量X1，X2，...,Xm的所有值， 的方差 都相同。

（3）误差项  是一个服从正态分布的随机变量，且相互独立，。

独立性意味着自变量 X1，X2，...,Xm 的一组特定值所对应的  与 X1，X2，...,Xm 任意一组其他值所对应的  不相关。正态性意味着对于给定的 X1，X2，...,Xm 的值，因变量y是一个服从正态分布的随机变量。

在一个具有n组观察值的样本中，第j组观察值（j=0,1,2,...,m）可表示为,便是M=m+1维空间中的一个点。

一个m元线性回归方程可给定为：

b0是都为0时y的点估计值

b1是在皆保持一定时，x1每增加一个单位对y的效用，称为不变（取常量）时x1对y 的偏回归系数（partial regression coefficient）。

在多元回归系统中，b0一般很难确定其专业意义，它仅是调节回归响应面的一个统计数；bi(i=1,2,...,m)表示了各个自变数xi对依变数y的各自效应，是这些各自效应的集合，代表多有自变数对依变数的综合效用。

（2）多元回归统计数的计算

（3）多元回归方程的估计标准误（参数的最小二乘估计）

满足=最小，Q叫做多元离回归平方和或多元回归剩余平方和。

因为系数b有m+1个统计数，所以自由度=n-(m+1)。多元回归的估计标准误：

             

总平方和（）=回归平方和（）+离回归平方和()

二、多元回归的假设测验

（1）多元回归关系的假设测验

测验m个自变数的综合对Y的效用是否显著。无效假设：,备择假设：不全为0

（2）偏回归关系的假设测验

多元回归关系的假设测验只是一个综合性的测验，它的显著表明自变数的集合和y有回归关系，并不排除个别乃至部分自变数和y没有回归关系的可能性。要准确评定各个自变数对y是否有真实回归关系，需进行偏回归系数的显著性做出假设测验。

在多元回归中的各个自变数彼此独立、完全无关时， 成立

当各自变数间存在相关（）时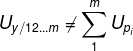， ，这是由于各自变数间的相关使其对y的效应产生了混淆。

若两个自变数 ,有显著的正相关（）,则的增大对于y的效应中包含有增大的效用，反之亦然（的大值和的大值相连，的小值和的小值相连）：

若两个自变数 ,有显著的负相关（）,则的增大对于y的效应中包含有减少的效用，的增大对于y的效应中包含有减少的效用：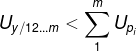                       

三、最优多元线性回归方程的统计选择

一个实际的多变数资料，既含有对Y 有显著效用的自变数，也含有无显著效应的自变数。在偏回归关系的假设测验中，通常一些bi显著，另一些bi不显著。

多元线性回归分析中，必须剔除没有显著效用的自变数，以使所得的多元回归方程比较简化而又能较准确地分析和预测Y的反应。剔除不显著自变数的过程称为自变数的统计选择，所得的仅包含显著自变数的多元回归方程，叫做最优的（在被研究的自变数范围内）多元线性回归方程。

由于自变数间可能存在相关，当m元线性回归中不显著的自变数有几个时，并不能肯定这些自变数对Y的线性效用不显著，而只能肯定偏回归平方和最小的那一个自变数不显著。当剔除了这个不显著且偏回归平方和最小的自变数后，其余原来不显著的自变数可能变为显著，而原来显著的自变数也可能变得不显著。为了获得最优方程，回归计算要一步一步做下去，直至所有不显著的自变数皆被剔除为止。这一统计选择自变数的过程称为逐步回归（stepwise regression）。

自变数统计选择的具体步骤：

（1）：m个自变数的回归分析，一直进行到偏回归的假设测验。若各自变数的偏回归皆显著，则分析结束，所得方程就是最优多元回归方程；若有一个或一个以上自变数的偏回归不显著，则剔除那个偏回归平方最小的自变数（设为）,进行第二步分析。

（2）：m-1个自变数的回归分析，也是一直进行到偏回归的假设测验。这一步的计算程序是将矩阵X中的Xp所占有的那一列（第p+1列）剔除，再由新 X 计算 X'X、 和 b 等，从而获得新的Q和。如果这一步仍有一个以上自变数的偏回归不显著，则再将偏回归平方和最小的那个变数（设为Xq）剔除，进入第三步分析。若第一步中有二个或更多个自变数的偏回归不显著，这一步可轮流试踢，直到找到最需剔除的一个，在进入第三步。

（3）m-2个自变数的回归分析，又一直进行到偏回归的假设测验。这一步的计算是在X中剔除所占的一行，其余过程同第二步。

如此重复进行，直至留下的所有自变数的偏回归都显著，即得最优多元线性回归方程。

四、自变数的相对重要性

最优多元线性回归方程中包含的自变数对依变数Y有显著作用，偏回归系数表示了对Y的具体效应。实践中还需评定这些显著自变数的相对重要性，以利于抓住关键因素，达到调整和控制依变数反应量的目的。

偏回归系数本身并不能反映自变数的相对重要性，原因：

（1）带有具体单位，单位不同则无从比较

（2）即使单位相同，若的变异度不同，也不能比较。

但若对标准化，在分子和分母分别除以Y和的标准差，就可消除单位和变异度不同不同的影响，获得一个表示对Y相对重要性的统计数——通径系数（path coefficient,记作 ）：

                                                    

通径系数  又称标准偏回归系数，统计意义：若增加一个标准差单位，Y将增加（）或减少（）个标准差单位。