数据结构四大查找——基本思想及python实现

查找表按照操作方式可分为：
1.静态查找表（Static Search Table）：只做查找操作的查找表。它的主要操作是：
①查询某个“特定的”数据元素是否在表中
②检索某个“特定的”数据元素和各种属性
2.动态查找表（Dynamic Search Table）：在查找中同时进行插入或删除等操作：
①查找时插入数据
②查找时删除数据

1. 顺序查找

顺序查找又称为线性查找，是一种最简单的查找方法，基本思想：从第一个元素m开始逐个与需要查找的元素x进行比较，当比较到元素值相同(即m=x)时返回元素m的下标，如果比较到最后都没有找到，则返回-1。适用于线性表的顺序存储结构和链式存储结构，该算法的时间复杂度为O(n)。
优缺点：
缺点：是当n 很大时，平均查找长度较大，效率低。
优点：是对表中数据元素的存储没有要求。另外，对于线性链表，只能进行顺序查找。

def sequential_search(list1, key):
   length = len(list1)
   for i in range(length):
       if list1[i] == key:
           return i
       else:
           return False

2. 二分查找

二分查找（Binary Search），是一种在有序数组中查找某一特定元素的查找算法。查找过程从数组的中间元素开始，如果中间元素正好是要查找的元素，则查找过程结束；如果某一特定元素大于或者小于中间元素，则在数组大于或小于中间元素的那一半中查找，而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空，则代表找不到。
时间复杂度：折半搜索每次把搜索区域减少一半，时间复杂度为 O(logn),空间复杂度：O(1)。

def binary_search(list1, key):
	low = 0
	high = len(list1) - 1
	time = 0
	while low < high:
		time += 1
		mid = int((low + high) / 2)
		if key < list1[mid]:
		     high = mid - 1
		elif key > list1[mid]:
		     low = mid + 1
		else:
		 # 打印折半的次数
		    print("times: %s" % time)
		    return mid
	print("times: %s" % time)
	return False

2.1腾讯：贪吃的小Q

思想：1:M个巧克力一个一个去验证太慢了，采用二分查找是为了加快速度

import math
n,m = map(int, input().split(" "))
def SumEat(e1,N):
    #计算N天一共吃了多少巧克力
    S = 0
    e = e1
    for i in range(0,N):
        S += e
        e = math.ceil(e/2)#(e+1)//2
    return S
 
def BinarySearch(N,M):
    #二分查找的变异，应用
    #创建[1,2,3,...,m]
    #以二分查找的方式，判断该位置的元素是不是满足第一天，调用SumEat函数
    if N == 1:
        return M
    low = 1
    high = M
    while low<high:
        mid  = (low+high+1)//2
        #满足就是mid
        if SumEat(mid,N)<=M:
            low = mid 
        else:#不满足的话就用mid前面的元素
            high = mid -1
    return low 
print(BinarySearch(n,m))

3. 插值查找

插值查找是根据要查找的关键字key与有序数组中最大最小记录的关键字比较后的查找方法，其核心就在于插值的计算公式 (key-a[low])/(a[high]-a[low])*(high-low)。时间复杂度O(logn),空间复杂度O(1)。

注意：
二分查找，将查找点的选择改进为自适应选择，可以提高查找效率。
对于表长较大，且关键字分布又比较均匀，插值查找算法的平均性能比折半查找要好的多。

def insert_search(list1, key):
	low = 0
	high = len(list1) - 1
	time = 0
	while low < high:
		time += 1
		 # 与折半查找唯一不同的地方
		mid = low + int((high - low) * (key - list1[low])/(list1[high] - list1[low]))
		if key < list1[mid]:
		     high = mid - 1
		elif key > list1[mid]:
		     low = mid + 1
		else:
		 # 打印折半的次数
		    print("times: %s" % time)
		    return mid
	print("times: %s" % time)
	return False

4. 斐波那契查找

斐波那契数列，又称黄金分割数列，指的是这样一个数列：1、1、2、3、5、8、13、21、····，在数学上，斐波那契被递归方法如下定义：F(1)=1，F(2)=1，F(n)=f(n-1)+F(n-2) （n>=2）。该数列越往后相邻的两个数的比值越趋向于黄金比例值（0.618）。
它也是二分查找的一种提升算法，通过运用黄金比例的概念在数列中选择查找点进行查找，提高查找效率，同样地，斐波那契查找也属于一种有序查找算法。

步骤：
1、给定一个斐波那契列表，使得最大元素>待查找的列表lis的长度
2、补全lis,使得lis的长度正好等于斐波那契列表的某个值，比如k
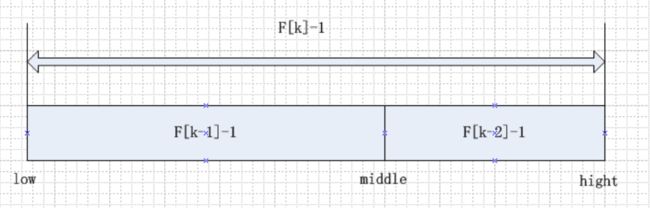
3、lis的两端就是最大索引F(k-1)-1，最小索引0，mid=low+F(k-1)-1
4、查找，判断待查找值key与lis[mid]的关系，再将lis的区间分为左右两块，只不过索引分的方式，是按斐波那契数列，F[k]-1=(F[k-1]-1)+(F[k-2]-1)+1，其中1表的mid索引。 

def fibonacci_search(lis, key):
    # 需要一个现成的斐波那契列表。其最大元素的值必须超过查找表中元素个数的数值。
    F = [1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,
    233, 377, 610, 987, 1597, 2584, 4181, 6765,
    10946, 17711, 28657, 46368]
    low = 0
    high = len(lis) - 1

    # 为了使得查找表满足斐波那契特性，在表的最后添加几个同样的值
    # 这个值是原查找表的最后那个元素的值
    # 添加的个数由F[k]-1-high决定
    k = 0
    while high > F[k]-1:
        k += 1
    print(k)
    i = high
    while F[k]-1 > i:
        lis.append(lis[high])
        i += 1
    print(lis)

    # 算法主逻辑。time用于展示循环的次数。
    time = 0
    while low <= high:
        time += 1
    # 为了防止F列表下标溢出，设置if和else
        if k < 2:
            mid = low
        else:
            mid = low + F[k-1]-1

        print("low=%s, mid=%s, high=%s" % (low, mid, high))
        if key < lis[mid]:
            high = mid - 1
            k -= 1
        elif key > lis[mid]:
            low = mid + 1
            k -= 2
        else:
            if mid <= high:
            # 打印查找的次数
                print("times: %s" % time)
                return mid
            else:
                print("times: %s" % time)
                return high
    print("times: %s" % time)
    return False
if __name__ == '__main__':
    LIST = [1, 5, 7, 8, 22, 54, 99, 123, 200, 222, 444]
    result = fibonacci_search(LIST, 444)
    print(result)

参考连接：
网址1
网址2