A2B:属性攻击图到贝叶斯攻击图的转化方法
A2B:属性攻击图到贝叶斯攻击图的转化方法
文章目录
-
- A2B:属性攻击图到贝叶斯攻击图的转化方法
-
- 由属性攻击图生成贝叶斯攻击图(AG-to-BAG)
- CVSS:原子攻击难度的度量指标和计算方法
- 结构转换
-
- 消除含圈路径
- 顺序结构
- a n d and and 结构
- o r or or 结构
- 混合结构
- 概率公式推导
-
- a n d and and 型节点
- o r or or 型节点
- t e m p temp temp 节点
- 攻击路径成功的概率
由属性攻击图生成贝叶斯攻击图(AG-to-BAG)
贝叶斯攻击图表示为 B A G < A , E , P > BAG
B A G BAG BAG 满足以下条件:
∀ E ⊆ A × A \forall E \subseteq A \times A ∀E⊆A×A 对 ∀ e ϵ E \forall e \epsilon E ∀eϵE ,都有 e = E i n ( e ) → E o u t ( e ) e = E_{in}(e) \rightarrow E_{out} (e) e=Ein(e)→Eout(e) ,其中 E i n ( e ) E_{in}(e) Ein(e) 表示原子攻击的结果属性,“ → \rightarrow →” 表示两个属性节点之间的因果关系。
条件独立假设:任意节点只与其父节点有关,与其非父节点均相互独立。
属性节点 A A A 是一个二元变量,只有两种状态, A A A 为 f a l s e false false 时表示攻击者已经获得该属性, A A A 为 t r u e true true 时表示攻击者还未获得该属性。
构建贝叶斯网络属性攻击图模型主要涉及两方面:模型网络结构的构建和节点发生概率的计算。
CVSS:原子攻击难度的度量指标和计算方法
原子攻击是利用网络中的 1 1 1 个脆弱点进行的一次攻击,可以将脆弱点被利用的难易度进行量化作为原子攻击难度的度量值,该值可以用通用漏洞评分系统 ( CVSS, common vulnerability scoring system ) 评分计算得到。
CVSS,全称 Common Vulnerability Scoring System,即“通用漏洞评分系统”,是一个“行业公开标准,其被设计用来评测漏洞的严重程度,并帮助确定所需反应的紧急度和重要度”。CVSS 是安全内容自动化协议(SCAP)的一部分,通常 CVSS 同 CVE 一同由美国国家漏洞库(NVD)发布并保持数据的更新。
CVSS 中基本评分 ( BM,base metrics) 部分描述的是脆弱点的基本属性,其中包含 6 6 6 个指标,前 3 3 3 个指标 是 AV ( access vector ) 、AC ( access complexity ) 、AU ( authentication ) ,用于描述脆弱点的可用性。 3 3 3 个 CVSS 指标的度量值根据可利用性分为 3 3 3 个等级: Low、Mid、High。分值越高,该脆弱点越容易被利用。由低到高,AV 值依次为 0. 359、0. 646、1. 0; AC 值依次为 0. 35、0. 61、0. 71; AU 值依次为 0. 45、0. 56、 0. 704。
在 CVSS 中,脆弱点的可用性指标定义为 E = 20 V C U ( 0 ≤ E ≤ 10 ) E = 20VCU( 0≤E≤10) E=20VCU(0≤E≤10)。 E x Ex Ex 的值越小,表示原子攻击的难度越大. 由于可用性与攻击难度成反比关系,因此根据这 3 个指标计算原子攻击的难度,用 D D D 表示相应原子攻击的难度,其值越大攻击难度越大,计算公式为
D = 1 2 V C U , D ≥ 1 D=\frac{1}{2VCU},D\ge 1 D=2VCU1,D≥1
结构转换
在初始的攻击图中,属性节点用矩形表示,原子攻击节点用椭圆形表示。当原子攻击的条件属性全部满足时,原子攻击才会发生;当原子攻击成功后会产生攻击影响,提高攻击者的攻击能力。用结果属性表示攻击者获得的攻击能力,原子攻击节点代表了前后节点的因果关系。
消除含圈路径
在攻击图中经常会出现攻击环路。由于攻击者是智能的,即攻击者不会重复获得已经具有的攻击能力,且随着攻击的进行攻击者的能力是单调递增的,因此在攻击图中出现攻击环是不合理的,也不便于理解攻击过程。
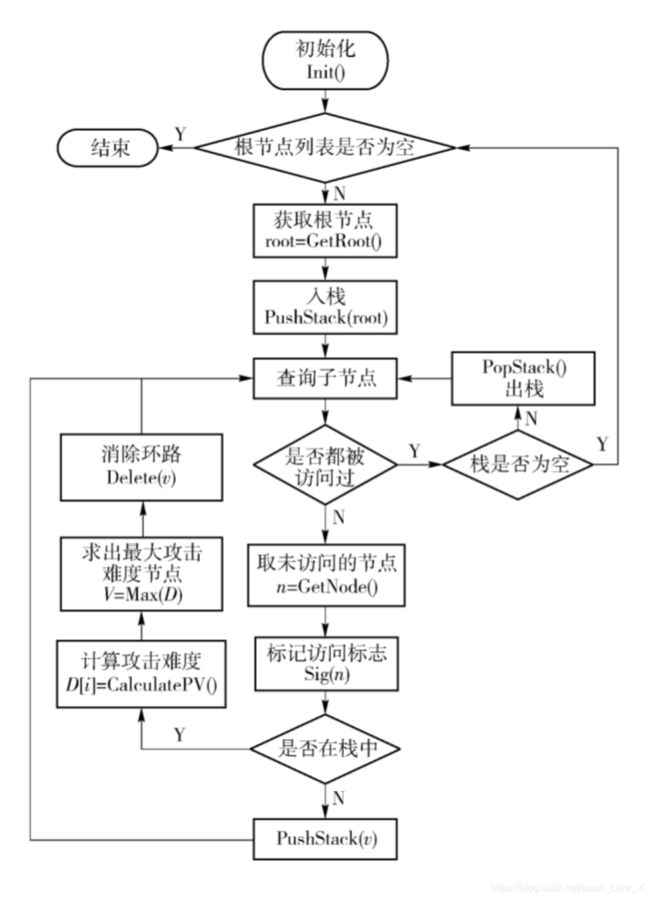
最难原子攻击消环算法思想:该算法的输入是一个可能含环路的攻击图,将攻击图的入口节点加入到根节点数组中,初始化一个栈用来存放找到的环路. 从一个入口根节点进行深度优先遍历,不断地访问子节点,将访问到的子节点进行标记并压入栈,直到不存在子节点或访问的节点在栈中已经出现为止。当子节点在栈中已经存在时,栈中存储了一个环路,此时计算环路中的原子攻击难度,找出难度最大的原子攻击节点,删除它的出边,消除环路。在遍历时,如果子节点不存在,则进行回溯,将栈中节点出栈,查询新的未被访问的子节点重复上述深度优先遍历过程。当栈为空时,则以该入口根节点为起始节点的遍历完成,从下一个新的入口根节点开始按上述方法遍历. 直到所有的入口根节点都遍历完,则整个攻击图消环完成,此时得到一个无环的攻击图。在该无环攻击图中,保留的原子攻击是最可能发生的,符合攻击的实际情况,即容易成功的原子攻击最可能被攻击者利用。
顺序结构
原子攻击节点变换过程中最简单一种就是顺序结构变换,在攻击图中原子攻击的条件属性和结果属性各只有 1 个. 在这种情况下,只需把原子攻击节点删除,用条件属性 a 1 a_1 a1 到结果属性 a 2 a_2 a2 的有向边表示原子攻击,即可转化为贝叶斯网络中的对应结构。
a n d and and 结构
由属性攻击图的定义可知,原子攻击节点的父节点之间是 a n d and and 的关系,只有当属性节点全部发生时原子攻击才会发生。对于有多个条件属性和 1 1 1 个结果属性的原子攻击节点,转化方法如下:将原子攻击节点删除,将每个条件属性到结果属性之间有 1 1 1 条有向边连接,用该有向边表示原子攻击,即条件属性和结果属性之间的因果关系。转化之后在贝叶斯网络结构中,条件属性之间的关系依然为 a n d and and 关系。
o r or or 结构
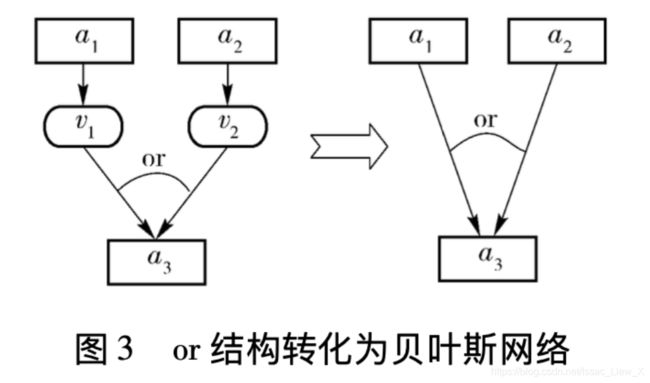
在攻击图中,属性节点的父节点之间是 o r or or 的关系,即父节点中的多个原子攻击只要有一个成功,攻击者就可获得结果属性。对于多个原子攻击有相同结果属性的情况,当原子攻击都只有一个条件属性时,转化方法如下:将原子攻击节点删除,条件属性到结果属性之间用有向边连接。在转化之后的贝叶斯网络中,条件属性之间仍为 o r or or 的关系。
混合结构
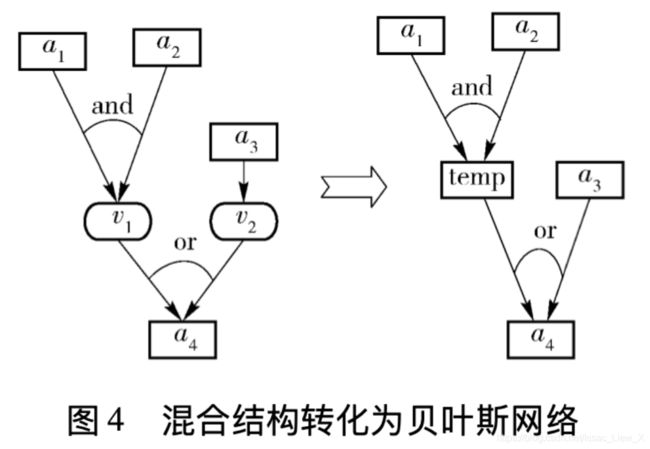
混合结构是同时具有 a n d and and 结构和 o r or or 结构,即多个原子攻击节点有相同的结果属性,且至少有 1 1 1 个原子攻击节点有多个条件属性。将具有 a n d and and 关系的原子攻击节点去掉,结果属性节点上就会有混合关系,因此需要引入一个隐含混合属性节点 t e m p temp temp。将 a n d and and 关系的入边指向 t e m p temp temp 节点,并且 t e m p temp temp 的出边指向结果属性,将只有 1 1 1 个条件属性的原子攻击节点删除,在条件属性到结果属性之间用 1 1 1 条有向边连接。
通过对攻击图中 4 4 4 种节点结构的转化,最终在得到的贝叶斯网络中只含有属性节点,有向边之间的关系只有 a n d and and 关系和 o r or or 关系,同时将原子攻击体现在贝叶斯网络的有向边上。
概率公式推导
a n d and and 型节点
计算图 2 2 2 的贝叶斯网络中 a 3 a_3 a3 节点属性的概率。
P ( a 3 ) = P ( a 3 ∣ a 1 , a 2 ) P ( a 1 , a 2 ) P(a_3)=P(a_3|a_1,a_2)P(a_1,a_2) P(a3)=P(a3∣a1,a2)P(a1,a2)
o r or or 型节点
P ( a 3 ) = P ( a 3 ∣ a 1 , a 2 ) P ( a 1 , a 2 ) + P ( a 3 ∣ a 1 , a 2 ˉ ) P ( a 1 , a 2 ˉ ) + P ( a 3 ∣ a 1 ˉ , a 2 ) P ( a 1 ˉ , a 2 ) P(a_3)=P(a_3|a_1,a_2)P(a_1,a_2)+P(a_3|a_1,\bar{a_2})P(a_1,\bar{a_2})+P(a_3|\bar{a_1},a_2)P(\bar{a_1},a_2) P(a3)=P(a3∣a1,a2)P(a1,a2)+P(a3∣a1,a2ˉ)P(a1,a2ˉ)+P(a3∣a1ˉ,a2)P(a1ˉ,a2)
t e m p temp temp 节点
P ( t e m p ) = P ( a 1 , a 2 ) P(temp)=P(a_1,a_2) P(temp)=P(a1,a2)
攻击路径成功的概率
给定贝叶斯攻击图中某属性节点变量,其参数满足 β \beta β 分布,即 θ ∼ B e [ α t , α f ] \theta \sim Be[\alpha t ,\alpha f ] θ∼Be[αt,αf],其中 α t \alpha t αt, α f \alpha f αf 称为 $\beta $ 分布的超参数。
在贝叶斯网络中属性节点之间的有向边代表原子攻击被利用的过程,原子攻击难度越大脆弱点被利用的概率就越低,两者成反比关系。因此,可以用原子攻击的难度代表属性节点之间的条件概率,定义条件概率为
P s = 1 D , 0 < P s < 1 P_s=\frac{1}{D},0
设攻击者要获得的目标属性为 o b j obj obj,在攻击路径上 o b j obj obj 的所有直接和间接父节点为 P r e ( o b j ) Pre( obj) Pre(obj) ,直接父节点为 D P r e ( o b j ) DPre( obj) DPre(obj) ,则目标节点受到攻击的概率为
P ( o b j ) = P ( o b j ∣ P r e ( o b j ) ) P ( P r e ( o b j ) ) P(obj) =P(obj|Pre(obj))P(Pre(obj)) P(obj)=P(obj∣Pre(obj))P(Pre(obj))
由于贝叶斯网络中条件独立性的假设,式 ( 5 ) ( 5) (5)可以改写为
P ( o b j ) = P ( o b j ∣ D P r e ( o b j ) ) P ( D P r e ( o b j ) ) P(obj) =P(obj|DPre(obj))P(DPre(obj)) P(obj)=P(obj∣DPre(obj))P(DPre(obj))
迭代式 ( 6 ) (6) (6) ,就可求得目标属性在该攻击路径中被攻击的概率。