卡塔兰数求解BST数目

首先，是在leetcode上遇到的一道求n个自然数可以组成的BST数目。

很自然的两种想法：

1. 模拟数的生成，时间复杂度会很高，编程困难

2.找出树生成数目的生成规律，直接按公式求解

然后，关于 卡塔兰数是什么，可以参见维基百科 http://zh.wikipedia.org/wiki/%E5%8D%A1%E5%A1%94%E5%85%B0%E6%95%B0

卡塔兰数是组合数学中一个常在各种计数问题中出现的数列。以比利时的数学家欧仁·查理·卡塔兰（1814–1894）命名。历史上，清代数学家明安图(1692年－1763年)在其《割圜密率捷法》最早用到“卡塔兰数”，远远早于卡塔兰^[1][2][3]。有中国学者建议将此数命名为“明安图数”或“明安图-卡塔兰数”^[4]。

卡塔兰数的一般项公式为 

前20项为（OEIS中的数列A000108）：1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190

性质[编辑]

C_n的另一个表达形式为 所以，C_n是一个自然数；这一点在先前的通项公式中并不显而易见。这个表达形式也是André对前一公式证明的基础。(见下文的第二个证明。)

递推关系

（*）

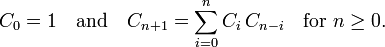它也满足

这提供了一个更快速的方法来计算卡塔兰数。

可以看到，卡塔兰数的递推关系式（*）符合 我们生成二叉树的关系 

f(0) = 1;

f(1) = 1;

f(2) = 2;

f(3) = 5;

.....

f(n) = f(n-1)*f(0) + f(n-2)*f(1) + ....f(0)*f(n-1)  //左右子树的所有情况；

编码如下：

#include 
using namespace std;

/*
	Given n,how many structurally BST's that store values 1..n?
	For example,
	Given n = 3,there are total of 5 unique BST's
*/
class Solution {
public:
	int numTrees(int n)
	{
		int ans = 1;
		for(int i = 1;i <= n;i++)
			ans = ans * 2 * (2*i-1)/(i+1);
		return ans;
	}
};
/*
f(0) = 0;
f(1) = 1;
f(2) = 2;
...
f(n) = f(n-1)*f(0)+f(n-2)*f(1)+...+f(0)*f(n-1)

性质：
	f(n+1) = 2*(2n+1)/(n+2)*f(n);
*/