Dijkstra算法 学习笔记

Dijkstra算法用于求最短路径，原理的话可以去网上搜搜，有一些讲得还是比较清楚的。笔者是在学openCV的时候接触到的，不过代码写出来似乎跟C++关系比较大，无妨，会用就好。

感谢 http://blog.csdn.net/yake827/article/details/50759977（转| 最短路径—Dijkstra算法和Floyd算法）和 http://blog.csdn.net/zjq2010014137/article/details/38370331（原 | Dijkstra算法（matlab)） 这两篇博文的作者。本文的话，系大半转小半原创吧。

在matlab里的实现与在c++中的实现有点不同，matlab里面矩阵行列从1开始，而C/C++的则从0开始，处理的时候有一些小细节要注意一下。另外，我C++也没学多少，有讲得不对的请勿见怪！好，闲话不说，上代码：

#include  
#include 
using namespace std;

//---------------------【全局变量声明】-----------------------
const int INF = 9999;

//const int SIZE = 4;
//int A[SIZE][SIZE] =
//{ { 0, 1, 3, 4 },
//{ 1, 0, 2, INF },
//{ 3, 2, 0, 5 },
//{ 4, INF, 5, 0 } };

const int SIZE = 6;
int A[SIZE][SIZE] = { { 0, 50, INF, 40, 25, 10 },
                      { 0, 50, INF, 40, 25, 10 },
                      { INF, 15, 0, 10, 20, INF },
                      { 40, 20, 10, 0, 10, 25 },
                      { 25, INF, 20, 10, 0, 55 },
                      { 10, 25, INF, 25, 55, 0 } };

//--------------------【函数声明部分】----------------------------
void Dijkstra(int v0, int e);

int main()
{
    Dijkstra(1, 4);

    return 0;
}

void Dijkstra(int v0, int e)
{
    v0 = v0 - 1, e = e - 1; //对数组与矩阵做不同处理

    //【1】-----------------变量声明部分------------------
    int n = SIZE;
    int dist[SIZE]; //存储起点到其他节点的最短距离
    int parent[SIZE]; //存储父节点
    bool S[SIZE]; //判断是否已存入该点到S集合中

    //【2】---------------进入Dijkstra算法------------------
    for (int i = 0; i < n; ++i)
    {
        dist[i] = A[v0][i];
        S[i] = false;  //初始都未用过该点
        if (dist[i] == INF)
            parent[i] = -1; //记录每一节点的上一节点
        else
            parent[i] = v0;
    }

    dist[v0] = 0;
    S[v0] = true;

    for (int i = 1; i < n; i++)
    {
        int mindist = INF;
        int index = v0; //找出当前未使用的点j的dist[j]最小值

        for (int j = 0; j < n; j++) {
            if ((!S[j]) && (dist[j] < mindist))
            {
                index = j; //u保存当前邻接点中距离最小的点的号码 
                mindist = dist[j];
            }
        }

        S[index] = true; //遍历后设置为已访问的点

        for (int j = 0; j < n; j++)
            //如果经过index节点，从起点到每个节点的路径长度更小，则更新 
            if (dist[index] + A[index][j] < dist[j])
            {
                dist[j] = dist[index] + A[index][j]; //更新dist 
                parent[j] = index; //记录前驱顶点 
            }
    }

    //【3】结果处理
    int distance = dist[e]; //最短距离

                            //回溯法 从尾部往前寻找搜索路径
    int t = e, p = -1,
        pathT[SIZE] = { -INF, -INF, -INF, -INF };
    while ((t != v0) && t >= 0) {
        pathT[--n] = t; //会有冗余，在下面会进行筛选
        p = parent[t];
        t = p;
    }

    //对应回矩阵
    vector<int> path;
    path.push_back(v0 + 1);
    for (int i = 1; i < SIZE; i++)
        if (pathT[i] >= 0)
            path.push_back(pathT[i] + 1);

    //【4】输出
    cout << "最短距离：" << distance << endl;
    cout << "路径为：";
    for (int i = 0; i < path.size(); i++)
        cout << path[i] << " -> ";
}

代码中注明了两个检测模板，分别是4X4和6X6的，main()方法里默认写了个用6X6的测试，结果如下：

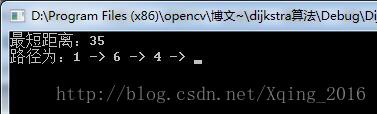
读者可以自行注释掉相应内容，在main里改改参数，可以试试4X4的测试。
最后，函数是没有写返回参数之类的，读者可自由变通，下面给了个参考：

//--------------------------【函数声明部分】----------------------------
void dijkstra(int v0, int e, vector<int> &road)

要存储包含路径的数组的话，用一般的数组长度不好确定，可考虑vector<>，C++有提供的，头文件声明一下就好。