机器学习-决策树之回归树案例（泰克尼克号）

一、决策树之回归树案例

1.导入相关库

import pandas  as pd 
from  sklearn.tree import DecisionTreeClassifier
import  matplotlib.pyplot as plt
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import  train_test_split,cross_val_score

2.读入数据，数据探索

data=pd.read_csv('data_1.csv')
data.head()
data.info()#分类器必须处理数值型的，需要把对象数据转换成数值型

结果显示：

RangeIndex: 891 entries, 0 to 890
Data columns (total 12 columns):
PassengerId    891 non-null int64
Survived       891 non-null int64
Pclass         891 non-null int64
Name           891 non-null object
Sex            891 non-null object
Age            714 non-null float64
SibSp          891 non-null int64
Parch          891 non-null int64
Ticket         891 non-null object
Fare           891 non-null float64
Cabin          204 non-null object
Embarked       889 non-null object
dtypes: float64(2), int64(5), object(5)
memory usage: 83.6+ KB

从结果显示，首先根据数据表显示对于人的名称这种的特征对结果应该影响是不大的，我们可以直接删除特征列（这样的数据需要自己对原数据进行理解），Cabin这样的缺失值太多了，这样可以考虑直接删除，Embarked缺失值就两个，占样本总数的比例也不大，这样的数据我么可以考虑直接删除样本，等等。。。。
3.对数据进行预处理

#删除缺失值过多的列，和观察判断来说和预测的y没有关系的列
#直接删除列
data.drop(["Cabin","Name","Ticket"],inplace=True,axis=1)
#处理缺失值，对缺失值较多的列进行填补，有一些特征只确实一两个值，可以采取直接删除记录的方法
#用均值填充年龄这个比较重要的数据
data["Age"] = data["Age"].fillna(data["Age"].mean())
# 对于Embarked这个特征趋势之比较少，可以删除该样本axis=0表示删除有缺失值的行
data = data.dropna(axis=0**加粗样式**)
#将分类变量转换为数值型变量
#将二分类变量转换为数值型变量
#astype能够将一个pandas对象转换为某种类型，和apply(int(x))不同，astype可以将文本类转换为数字，用这
个方式可以很便捷地将二分类特征转换为0~1
data["Sex"] = (data["Sex"]== "male").astype("int")
#将三分类变量转换为数值型变量（注意匿名函数的用法）
labels = data["Embarked"].unique().tolist()
data["Embarked"] = data["Embarked"].apply(lambda x: labels.index(x))
#查看处理后的数据集
data.head()

有一个问题：
# [‘Embarked’]注意这里面的几个单个值是独立的才能直接这样做，对于有顺序和大小的应该怎样进行编码呢？
注意事项：

值得注意的是，data['列名']这种获取列的方法不太准确，可以考虑data.iloc[],和data.loc[]
data.iloc[]是索引值获取
data.loc[] 是标签进行获取

4. 提取标签和特征矩阵，分测试集和训练集

# 将数据和标签进行分裂
x=data.loc[:,data.columns!='Survived']
y=data.loc[:,data.columns=='Survived']
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.3)
#注意这样的索引就会乱了，最好将数据进行重新索引,方便后面操作
#这个操作就完成了将索引从0开始
for  i in [x_train,x_test,y_train,t_test]:
    i.index=range(i.shape[0])

5.建立模型和预测

clf=DecisionTreeClassifier(random_state=25)
clf=clf.fit(x_train,y_train)
score=clf.score(x_test,y_test)
score

结果：0.7303370786516854

用交叉验证试试

#用训练集的数据的下过不是特别的好，我们现在来试试用交叉验证
clf=DecisionTreeClassifier(random_state=25)
score=cross_val_score(clf,x,y,cv=10).mean()
score

结果：0.74696118488253327
下面看一下学习曲线，来观察效果

#效果不是特别好，现在我们来画一下学习曲线
tr=[]
te=[]
for i in range(10):
    clf=DecisionTreeClassifier(random_state=25
                              ,max_depth=i+1
                              )
    clf=clf.fit(x_train,y_train)
    score_tr=clf.score(x_train,y_train)
    score_te=cross_val_score(clf,x,y,cv=10).mean()
    tr.append(score_tr)
    te.append(score_te)
print(max(te))
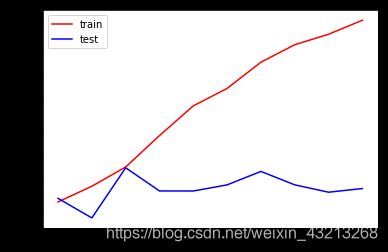
plt.plot(range(1,11),tr,color='red',label='train')
plt.plot(range(1,11),te,color='b',label='test')
plt.xticks(range(1,11))
plt.legend()
plt.show()

结果如下所示：

0.81438968335

试试调参

'''这里为什么使用“entropy”？因为我们注意到，在最大深度=3的时候，模型拟合不足，在训练集和测试集上的表现接
近，但却都不是非常理想，只能够达到83%左右，所以我们要使用entropy。'''
tr=[]
te=[]
for i in range(10):
    clf=DecisionTreeClassifier(random_state=25
                              ,max_depth=i+1
                              ,criterion='entropy'#加入该参数再看看效果哦
                              )
    clf=clf.fit(x_train,y_train)
    score_tr=clf.score(x_train,y_train)
    score_te=cross_val_score(clf,x,y,cv=10).mean()
    tr.append(score_tr)
    te.append(score_te)
print(max(te))
plt.plot(range(1,11),tr,color='red',label='train')
plt.plot(range(1,11),te,color='b',label='test')
plt.xticks(range(1,11))
plt.legend()
plt.show()

结果：0.816662410623

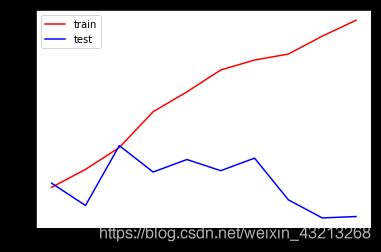
结果表现的好一些了。但是模型还是不太理想，我们需要进行调参，用什么方法调整所有的参数呢？下面试试网格搜索吧。
5.用网格搜索来调整参数

import numpy as np
# parameters是一串参数和这些参数对应的我们希望网格搜索来搜索的参数 的取值范围
parameters={'criterion':('gini','entropy')
           ,'splitter':('best','random')
           ,"max_depth":[*range(1,10)]
           ,'min_samples_leaf':[*range(1,50,5)]
           ,'min_impurity_decrease':[*np.linspace(0,0.5,20)]#信息增益的最小值
           }
clf=DecisionTreeClassifier(random_state=25)
GS=GridSearchCV(clf,parameters,cv=10)
GS.fit(x_train,y_train)
GS.best_params_#从我们输入的参数和参数取值的列表中，返回最佳组合

GS.best_score_#网络搜索后的模型的评判标准
#网格搜索也太慢了吧哈哈哈

结果：
0.82636655948553051

注意：
网格搜索的一个缺点就是不能自行删除一些参数，可能结果还没有进自己调整部分参数结果高