图像去雾算法学习笔记1——何凯明博士基于暗通道先验的单幅图像去雾算法公式推导

首先简单自我介绍一下，本人现在是国内某211大学2019级博士研究生，计算机科学与技术专业，研究方向和兴趣包括深度学习（CV）、图像处理、菌群仿生优化算法、元胞自动机等，愿与大家分享自己的学习心得！现刚入学1个多月，先从图像去雾算法开始学起。
  说到图像去雾算法，不得不提大牛何凯明博士，圈内都知道他的：
何凯明博士，本科毕业于清华大学基础科学班。他是2006年微软小学者奖学金获得者之一，同时也是2003年广东省高考状元。2007年清华大学毕业之后开始在微软亚洲研究院（MSRA）实习，2011年香港中文大学博士毕业后正式加入MSRA，目前在Facebook AI Research (FAIR)实验室担任研究科学家。曾以第一作者身份拿过两次CVPR最佳论文奖Best Paper Award （2009和2016）——其中2016年CVPR最佳论文为图像识别中的深度残差学习（Deep Residual Learning for Image Recognition）。
     我现在看的是他2009年的CVPR论文：《Single Image Haze Removal Using Dark Channel Prior》在中国知网、百度学术上都有下载的。CVPR的中文名是计算机视觉与模式识别会议，是计算机视觉领域最顶尖的国际会议之一。2009年的CVPR共收到约1450篇投稿，其中393篇文章被接收，接收率为26%。只有一篇文章被选为那年的最佳论文。这是CVPR创立25年以来首次由中国人获得这个奖项。这篇文章是他在微软亚洲研究院形象计算组实习的时候完成的，也是他个人真正意义上写的第一篇论文。
他根据Dark Object Subtraction原理通过大量实验发现局部找最暗点进行均匀去雾有很好的效果。
   由此得到对于一个无雾图像，每个局部区域都很有可能有一些暗的地方，换言之，至少一个颜色通道会有很低的值、或黑色东西。
看了他的论文，准备写点笔记，这是我的第一篇笔记。

---

一、简单有效的图像去雾技术

    这篇论文研究的问题是图像的去雾技术，它可以还原图像的颜色和能见度，同时也能利用雾的浓度来估计物体的距离，这些在计算机视觉上都有重要应用（例如三维重建，物体识别）。但是之前人们还没找到简单有效的方法来达到这个目的。在这篇论文里，他们找到了一个非常简单的，甚至说令人惊讶统计规律，并提出了有效的去雾方法。

   与之前的方法不同，他们把注意力放到了无雾图像的统计特征上。他们发现，在无雾图像中，每一个局部区域都很有可能会有阴影，或者是纯颜色的东西，又或者是黑色的东西。因此，每一个局部区域都很有可能有至少一个颜色通道会有很低的值。他们把这个统计规律叫做Dark Channel Prior（暗通道先验或暗原色先验）。直观来说，Dark Channel Prior认为每一个局部区域都总有一些很暗的东西。这个规律很简单，但在他们研究的去雾问题上却是本质的基本规律。

     由于雾总是灰白色的，因此一旦图像受到雾的影响，那么这些本来应该很暗的东西就会变得灰白。不仅如此，根据物理上雾的形成公式，他们还能根据这些东西的灰白程度来判断雾的浓度。因此，他们提出的Dark Channel Prior能很有效地去除雾的影响，同时利用物的浓度来估算物体的距离（深度）。

     简单理解：仔细想想我们可以确定有这样一个统计规律：对于大多数没有雾的图像来说，它的任意一个像素点中的R，G，B值至少有一个是非常低的；（这个挺好理解的，如果R,G,B值都偏高，那么该像素显然有向白色过度的趋势）把每个像素中“偏暗”的值（通道）以一定的方式集合起来就构成了一幅图片的暗通道图；正式基于这样的一个想法和统计的规律（可以把这个统计规律当作一条定理），何博士提出了去雾的算法，该算法在大量的户外有雾图片的应用中得以验证其准确性；并且在去雾的过程中，他们也同时得到了原图的景深图片，因为雾的厚度一定程度上代表了景深。

为了验证上述提到的统计规律，何博士对5000张无雾图的暗通道的强度进行了统计，可以发现暗通道图中大部分像素都是0，而且全部像素都集中于0-50之间，可以说暗通道图是稀疏的，这一点对于我们下边的公式推导至关重要

---

二、相关背景和公式
    看了何凯明博士的这篇论文，以及我近期看的其他论文，我总结了图像去雾的三种方法：
1、图像增强技术。常用于雾天图像清晰化处理的图像增强方法，包括直方图均衡、对数变换、幂律变换、锐化、小波变换等，这些都是图像处理中常用来提高对比度或者突出图像特征的方法。但严格的说，这一类方法并不研究雾气对图像影响的原理，并非去除图像中的雾，而是应用图像增强方法，对图像作清晰化处理。
2、基于物理模型的图像去雾算法对图像进行复原。图像复原通过分析雾图降质机理，建立图像散射模型（即建立方程），充分利用图像退化的先验知识或假设，实现场景复原（即求解方程）。说到这里，就不得不提经典的描述有雾图像的散射模型：

其中t(x)可以表示为：

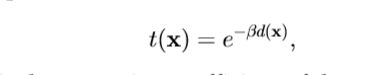
0<=t(x)<=1
这个模型也是何凯明博士的这篇论文中用到的。
3、还有就是基于最近几年火爆的深度学习方法。如利用随机森林学习回归模型估计透射率的值，利用卷积神经网络构造端到端的去雾网络等。这个是我下一步的研究方向啊。

三、我目前学习的主要方法：基于物理模型的去雾算法复原图像
      对于上面的描述有雾图像的散射模型，其中x为像素空间坐标，I(x)为观测的强度，也就是理解为实际拍摄的有雾图像，J(x)为场景辐射，也就是理解为清晰无雾的图像（就是我们要复原的清晰图像），t是介质传输率，描述的是未被大气颗粒物（雾、霾等悬浮颗粒）散射而到达照相机的那部分光,A是全局大气光，也就是整体大气光值，可以理解为就是太阳光。J(x)t(x)称为直接衰减项，描述了场景辐射照度在介质中的衰减，它随场景深度呈指数性衰减，A(1-t(x))称为大气光幕，用来描述场景成像中加入的大气散射光，这个部分是太阳光经过微粒散射之后参与到成像光路中的部分，它造成了场景的模糊和颜色的失真。这个模型我们要做到的去雾就是从实际拍摄得到的I(x)去求解出J(x)、A和t。 很明显，如果对于一个含N个像素的彩色图片，每个像素有3个通道（RGB）值，那一共就有3N个方程式，但是未知量包括3N个J(x)、N个t(x)、3个A值，一共是4N+3个未知量，用3N个方程解4N+3个未知量，明显就是个“病态方程”。但目前的研究都不是精确的求解，因为这是一个多未知数的“病态方程”，我们只能去估计参数A和t(x),最关键的就是估计介质传输率t(x),然后从I(x)中恢复J(x).
        下面对这个散射模型两边对x求梯度（偏导）得到：

         这里面是对一个色块（patch）求的，其中假设t是均匀的，所以t和x无关，就直接作为系数提出来，然后A(1-t(x))与x无关就变成了0，又当t<1时，所以得到了上式。原文的描述： For a patch with uniform transmission t, the visibility (sum of gradient) of the input image is reduced by the haze since t<1。The transmission t in a local patch is estimated by maximizing the visibility of the patch under a constraint that the intensity of J(x） is less than the intensity of A.
四、何凯明博士这篇论文的核心思想——暗通道先验
    首先看看暗通道先验是什么：
    在绝大多数非天空的无雾图像的局部区域里，某一些像素总会有至少一个颜色通道具有很低的值。换言之，该区域光强度的最小值是个很小的数。我们给暗通道一个数学定义，对于任意的输入图像J，其暗通道可以用下式表达：

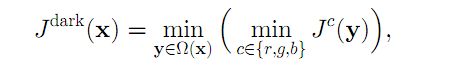
式中$J^c$表示彩色图像的每个通道 ，Ω(x)表示以像素X为中心的一个窗口，代表像素点X周围的小区域即滤波器。等式左边即为暗通道图，等式右边：C代表R，G，B中的某一通道，x代表图中某一像素点； 这个公式的意义用代码表达也很简单，首先求出每个像素RGB分量中的最小值，存入一副和原始图像大小相同的灰度图中，然后再对这幅灰度图进行最小值滤波（下一篇博文我将介绍滤波的原理），滤波的半径由窗口大小决定，一般有WindowSize = 2 * Radius + 1;
这个公式的意思可以这样理解：首先取原图每一个像素点中最小的通道值，这样就可以得到一副灰色的图了，然后对这个灰色的图进行最小值滤波（滤波窗口代表了Ω(X)）就得到了暗通道图。

     暗通道先验的理论指出：

     实际生活中造成暗通道中低通道值主要有三个因素：a)阴影等。汽车、建筑物和城市中玻璃窗户的阴影，或者是树叶、树与岩石等自然景观的投影；b)色彩鲜艳的物体或表面等，在RGB的三个通道中有些通道的值很低（比如绿色的草地／树／植物，红色或黄色的花朵／叶子，或者蓝色的水面）；c)颜色较暗的物体或者表面，例如灰暗色的树干和石头。总之，自然景物中到处都是阴影或者彩色，这些景物的图像的暗原色总是很灰暗的。原文的表述：The low intensity in the dark channel is mainly due to three factors: a) shadows, e.g., the shadows of cars, buildings, and the inside of windows in cityscape images, or the shadows of leaves, trees, and rocks in landscape images; b) colorful objects or surfaces, e.g., any object with low reflectance in any color channel (for example, green grass/tree/plant, red or yellow flower/leaf, and blue water surface) will result in low values in the dark channel; c) dark objects or surfaces, e.g., dark tree trunks and stones. As the natural outdoor images are usually colorful and full of shadows, the dark channels of these images are really dark!
论文中列举的暗通道图：
     作者随机选取了5000张无雾图片，并手工切除了天空区域，重新调整图像大小，使得最大宽度和高度像素为500像素，并使用1515的色块大小去计算暗通道。
     原文描述：Among them, we randomly select 5,000 images and manually cut out the sky regions. The images are resized so that the maximum of width and height is 500 pixels and their dark channels are computed using a patch size 1515. Fig. 4 shows several outdoor images and the corresponding dark channels.

     由上述几幅图像，可以明显的看到暗通道先验理论的普遍性。在作者的论文中，统计了5000多副图像的特征，也都基本符合这个先验，因此，我们可以认为这其实时一条定理，但是基于统计得出的结论。 有了这个先验，接着就需要进行一些数学方面的推导来最终解决问题。
五、用这个暗通道先验解上面那个“病态方程”
重新拿出这个要求解的病态方程-大气散射模型：

稍作变形（归一化）：

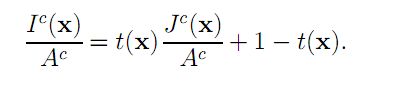
上标C表示R/G/B三个通道的意思。
     首先假设在每一个窗口内透射率t(x)为常数，定义他为$\tilde{t}(x)$ ,并且A值已经给定，然后对上式两边求两次最小值运算（用的是最小值滤波），得到下式：

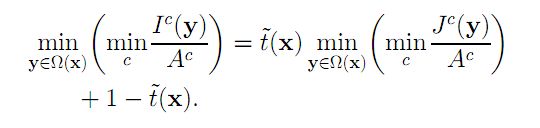
上式中，J是待求的无雾的图像，根据前述的暗通道先验理论有：

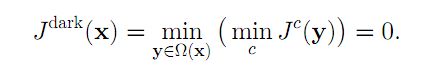
因此，可推导出：

把这个公式带入到上面的最小值滤波后的公式得到：

这就是透射率t的预估值。
     在现实生活中，即使是晴天白云，空气中也存在着一些颗粒，因此，看远处的物体还是能感觉到雾的影响，另外，雾的存在让人类感到景深的存在，因此，有必要在去雾的时候保留一定程度的雾，这可以通过在式（11）中引入一个在[0,1] 之间的因子，则上面的公式修正为：

该论文中所有的测试结果依赖于： ω=0.95。

     上述推论中都是假设全球达气光A值时已知的，在实际中，我们可以借助于暗通道图来从有雾图像中获取该值。具体步骤如下：
1） 从暗通道图中按照亮度的大小取前0.1%的像素。

2） 在这些位置中，在原始有雾图像I中寻找对应的具有最高亮度的点的值，作为A值。 到这一步，我们就可以进行无雾图像的恢复了。大气散射模型公式可知： J = ( I - A)/t + A
现在I,A,t都已经求得了，因此，完全可以进行J的计算。
当投射图t 的值很小时，会导致J的值偏大，从而使淂图像整体向白场过度，因此一般可设置一阈值T0，当t值小于T0时，令t=T0，本文中所有效果图均以T0=0.1为标准计算。
     因此，最终的恢复公式如下：

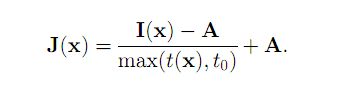
　      要获得更为精细的透射率图，何博士在文章中提出了了soft matting方法，能得到非常细腻的结果。 以下是他论文中的效果图： 　

交流扣扣群：533209464（备注“学习”），如果大家有需要，我就录制完整的去雾算法视频讲解课程