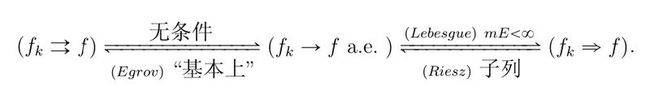[实变函数]4.4 依测度收敛
1 以前学过 $$\bex \mbox{ 点态收敛},\quad \mbox{ 一致收敛}, \eex$$
本节将用测度引进另外一种收敛概念---``依测度收敛'': $$\beex \bea &\quad (f_k\ra f)\ (\mbox{菲赫金哥尔茨的记号})\\ &\lra \forall\mbox{ 误差 }\sigma>0,\ E[|f_k-f|\geq \sigma]\mbox{ 虽然可能很多, 但其测度 }\to 0\ (k\to\infty). \eea \eeex$$
2 依测度收敛: $$\bex (f_k\ra f)\lra \forall\ \sigma>0,\ \lim_{k\to\infty}m [|f_k-f|\geq \sigma]=0. \eex$$
3 依测度收敛与 $\ae$ 收敛的区别:
(1) 依测度收敛但不收敛的例子.
(2) $\ae$ 收敛但不依测度收敛的例子: $$\bex f_k(x)=\sedd{\ba{ll} 1,&x\in (0,n]\\ 0,&x\in (n,+\infty) \ea}. \eex$$
4 依测度收敛与 $\ae$ 收敛的联系:
(1) (Riesz 定理) $$\bex (f_k\ra f)\ra \exists\ \sed{k_j},\st f_{k_j}\to f, \ae. \eex$$
证明: $$\beex \bea &\quad f_k\ra f\\ &\ra \forall\ \sigma>0,\ \lim_{k\to\infty}m [|f_k-f|\geq \sigma]=0\\ &\ra \forall\ \sigma>0,\ \forall\ \ve>0,\ \exists\ k,\st m(E[|f_k-f|\geq \sigma])<\ve\\ &\ra \forall\ s\in\bbZ^+,\ \exists\ k_s,\st mE_s<\frac{1}{2^s}\quad\sex{E_s=E\sez{|f_{k_s}-f|\geq \frac{1}{2^s}}}\\ &\ra m\sex{\cup_{s=1}^\infty E_s}<\sum_{s=1}^\infty \frac{1}{2^s}=1<\infty\\ &\ra m \sex{\varlimsup_{s\to\infty}E_s}=0\quad\sex{\mbox{Page 75 T 11}}\\ &\ra f_{k_s}\to f\mbox{ 于 }E\bs \varlimsup_{s\to\infty}E_s=\cup_{m=1}^\infty \cap_{s=m}^\infty E\sez{|f_{k_s}-f|<\frac{1}{2^s}}. \eea \eeex$$
(2) (Lebesgue) 设 $mE<\infty$, $$\bex \ae\mbox{ 有限的可测函数列 }\sed{f_k}\ae \mbox{ 收敛于 }\ae\mbox{ 有限的函数 }f. \eex$$ 则 $$\bex f_k\ra f. \eex$$
证明: $$\beex \bea &\quad m\sex{\cup_{j=1}^\infty \cap_{N=1}^\infty \cup_{k=N}^\infty E\sez{|f_k-f|\geq \frac{1}{j}}}=0\\ &\ra \forall\ j\in\bbZ^+,\ \lim_{N\to\infty} m\sex{\cup_{k=N}^\infty E\sez{|f_k-f|\geq \frac{1}{j}}}=0\\ &\ra \forall\ j\in\bbZ^+,\ \lim_{N\to\infty} m\sex{E\sez{|f_N-f|\geq \frac{1}{j}}}=0. \eea \eeex$$ 注: Lebesgue 定理中 $mE<\infty$ 是必须的. 否则有反例: $$\bex f_k(x)=\sedd{\ba{ll} 1,&x\in (0,n]\\ 0,&x\in (n,+\infty) \ea}. \eex$$
5 依测度收敛的极限的唯一性 (在 $\ae$ 意义下): $$\bex (f_k\ra f,\ f_k\ra g)\ra f=g,\ae. \eex$$ 证明: $$\beex \bea E[|f-g|>0] &=\cup_{j=1}^\infty E\sez{|f-g|\geq\frac{1}{j}}\\ &=\cup_{j=1}^\infty E\sez{|(f_k-f)-(f_k-g)|\geq \frac{1}{j}}\\ &\subset \cup_{j=1}^\infty \sex{E\sez{|f_k-f|\geq\frac{1}{2j}} \cup E\sez{|f_k-g|\geq\frac{1}{2j}}}. \eea \eeex$$
6 各种收敛态的关系总结:
7 作业: Page 95, T 15.