数字信号处理——单位冲击响应
作者：KE meng
链接：https://www.zhihu.com/question/29461110/answer/93942919
来源：知乎
著作权归作者所有，转载请联系作者获得授权。
链接：https://www.zhihu.com/question/29461110/answer/93942919
来源：知乎
著作权归作者所有，转载请联系作者获得授权。
那么,首先我们来看看比较重要的"
线性时不变系统":
所谓线性时不变系统,首先要线性,然后要时不变:
所谓 线性,指的是如果任意输入x输入系统得到y, 那么x*k输入系统,应该得到y*k,
比如,"乘100"就是个线性系统,因为例如以5为输入得到输出500,而5*6为输入得到
3000 == 5*100*6. 而"平方"则不是线性系统,因为以5为输入得到25,而5*6得到的结果是
30*30 != 5*5*6.
线性时不变系统的另一个特性就是 叠加性, 即假如x进入系统得到结果f(x), 那么若x=a+b,
必有f(x) = f(a) + f(b).
还有就是 时不变,时不变指的是若一个输入x得到信号y,那么一个经过了延迟的x得到的
也只是一个被延迟过的y.而不能是其他值.
举个不太恰当的例子,假设有一个火车站, 今天你去买票买到了今天的票, 明天你去买到了明天的票,那么这个火车站就是个时不变系统,假如今天你去买票买到了今天的票,明天你去买到了大后天的票,那么这个火车站就不是时不变系统.
说了半天了,进入正题,脉冲信号有啥用?
注: 为了方便理解,以下全部使用离散信号:
假设我们有个连续信号,我们不妨对它进行采样,为了方便讲解我把采样率弄低了一点:
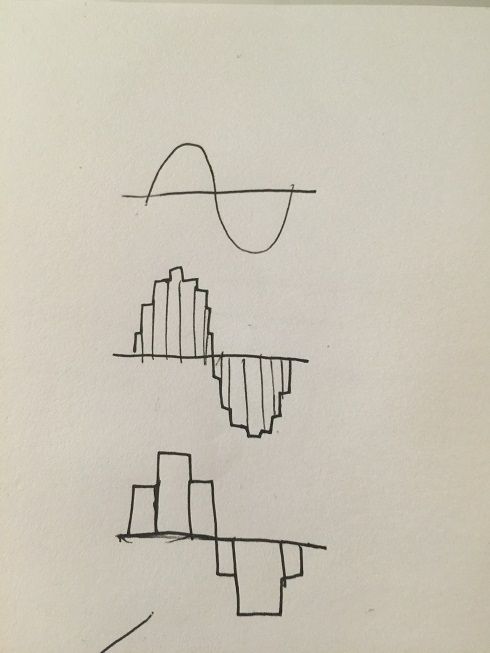
可以看到,采样之后得到了一个比较"方块"的波形. 那么, 我们把这个离散化的波形切成6份:
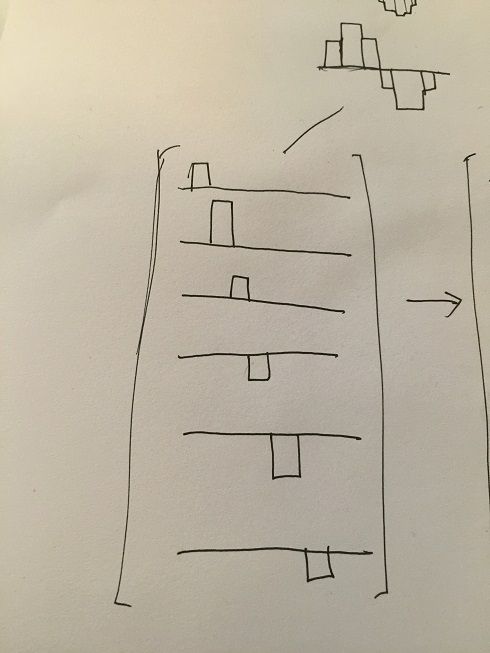
好了,我们得到了6个波形,那么我们会发现这6个波形是大小不一的,我们将其转换为大小
一致的,归一化的6个波形分别乘以不同的系数:
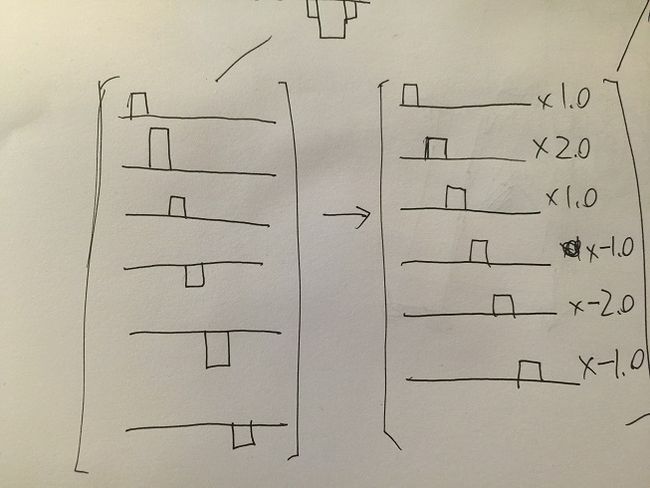
好,那么我们又发现,这六个波形现在大小一样了,只不过互相之间有一些延迟,不要紧,我们把延迟
用系数代替:
发现什么没? 最开始的波形实际上就是6个不同振幅系数,不同延迟系数的脉冲波的线性组合.
但是,即使这样也不能证明脉冲就有用了, 就算波形能被分解成不同振幅系数,不同延迟系数的线性组合, 那又怎么样呢?
回忆一下我们最开始所说的线性时不变系统的定义, 就会发现, 一个信号x(t)输入系统,得到输出y(t),那么k*x(t)输入系统就会得到k*y(t), x(t-T)输入系统就会得到y(t-T),那么,假如我们把刚才的六个信号输入线性时不变系统,就会得到以下内容:
实际上,我们根本不需要让这六个信号都输入系统,由于线性时不变,我们只需要让这六个信号中的任意一个信号归一化,对齐到0时刻,进入系统,再对输出乘以不同系数,延迟不同时间,就得到了所有的输出.
故事到这里还没结束, 还记得咱们这六个信号怎么来的吗? 没错, 是从一个波形上切下来的;
然后,由于线性系统的 叠加性,这个波形的输出就等于那六个信号的输出之和. 而那六个信号又
等于不同延迟,不同系数的脉冲信号, 因此我只需将脉冲信号输入系统,就可以得到完整波形输入
系统后能得到的全部内容---- 无非就是一堆不同延迟,不同系数的脉冲信号的输出之和:
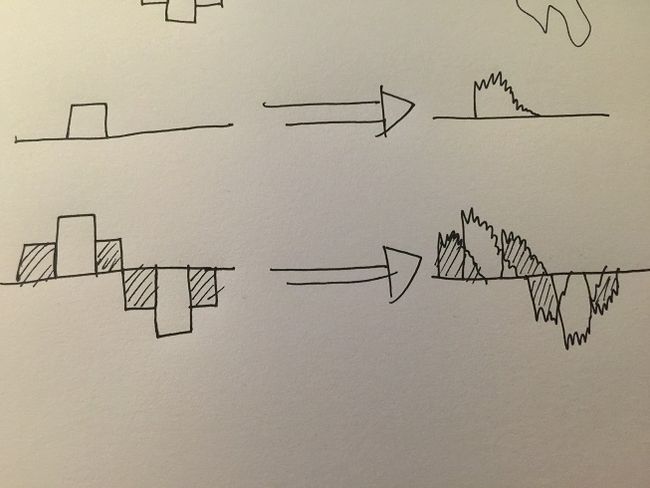
因此对于线性时不变系统来说, 只需要拿脉冲信号"bi"一下,别的什么都不需要研究,就能得到这个线性时不变系统的全部信息了.
//------------------------- 更新 ------------------------------------
再来我们看看卷积:
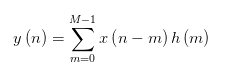
我们知道拿着脉冲对着线性时不变系统H "哔"一下,得到的结果h(t),即冲击响应. 再用这个冲击响应和信号x做卷积,得到的结果y就是x经过线性时不变系统H的结果. 那么问题来了:
1. TM凭什么!
2. 卷积为啥定义成这个德行???
我是从泛函那边儿学过来的,刚看卷积时简直匪夷所思,为啥x和h要反着乘???
跟内积定义的一样不行吗? 其实弄明白上文中脉冲的作用,就不难理解卷积的形式了:
上文中我们知道,只要知道了脉冲经过线性时不变系统的输出结果,就可以用这个输出结果附上系数,延迟,累加出任意信号x的输出y.那么这个累加的过程,如图:
(示意图,明白意思就行了....)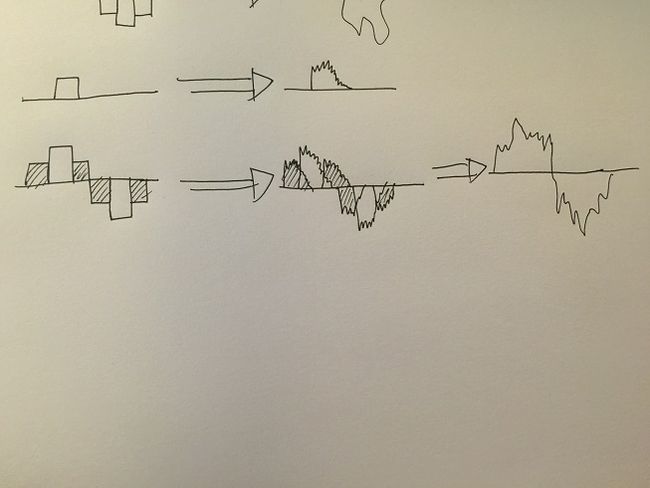
(示意图,明白意思就行了....)
图是好画,可是转换成数学形式就有点麻烦了,为了更规范和精确一点,我们不再使用大方块代表脉冲波,而是使用一根棍儿来代表脉冲波:
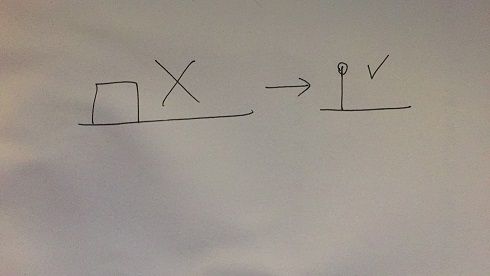
那么,这根棍儿经过了一个线性系统H,得到输出h:
其中,h(0)到h(4)代表着这个h在离散横轴0,1,2,3,4点上的值.
还拿本答案最开始的那个波形举例,只不过将大方块换成棍子:
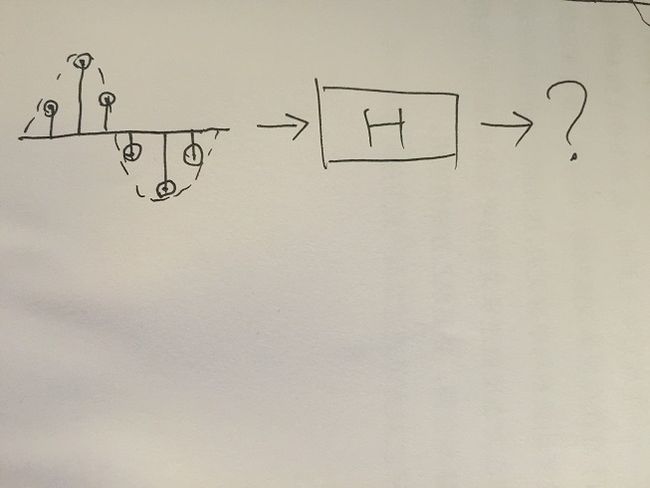
根据前文,我们已经知道这个x的输出结果无非就是一堆乘以系数,延迟过的h之和,现在要求出x所对应的输出y.先不看前面的,只考虑y(5)的位置,这个位置的值等于多少呢?
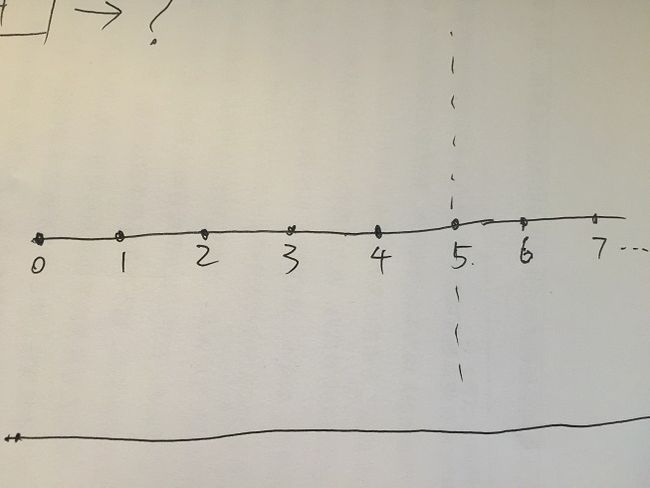
首先,将脉冲响应h延迟到y(5)的位置上:
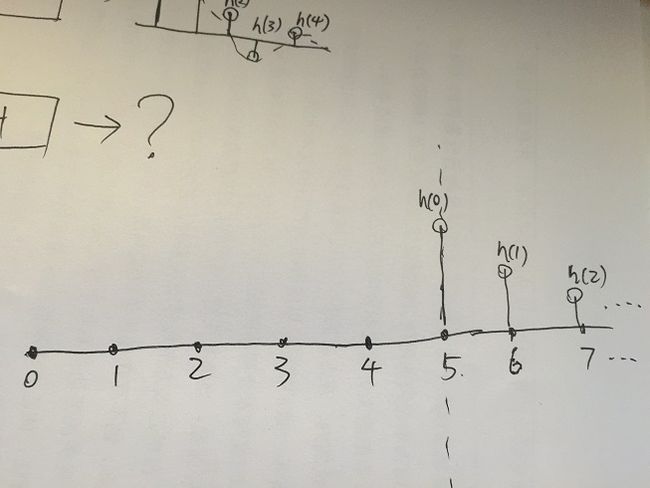
可以看到y(5)上的h已经落座了,但是不要慌,我们光延迟了h,还没乘系数呢, 那么在y(5)的位置上h的系数为多少呢? 因为h是标准化的,最大值为1,所以在y(5)的位置上h的系数就是x(5)啊:
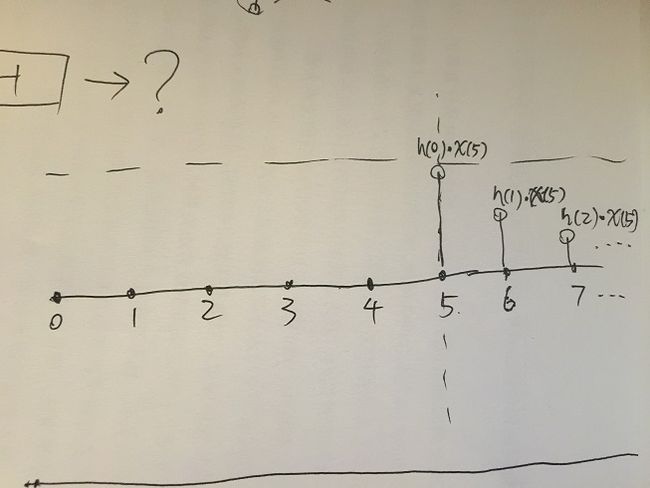
好了,y(5)位置的y值就考虑完毕了........吗? 并没有! 因为y(4)的位置上也有一个h! h是有长度的! 所以h会"拖到"y(5)的位置上, 而且y(4)上的h, 其系数就是x(4). 它们要加起来的啊:
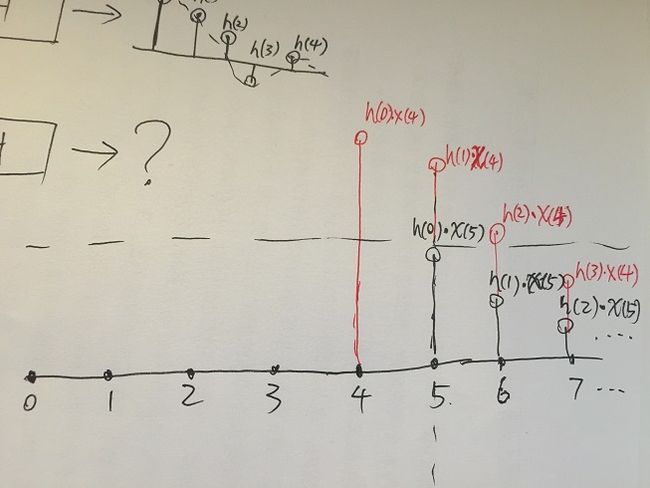
然后呢? 还有y(3)上的h呢:
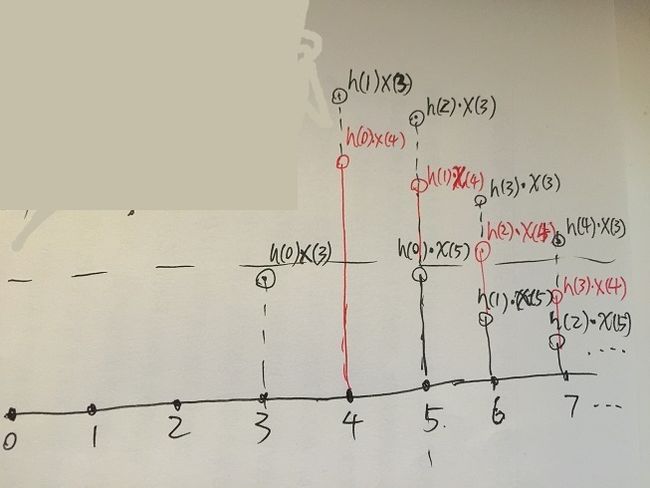
好了,y(2),y(1)上的h我就先不画了,咱们就盯着y(5)看,仔细看:
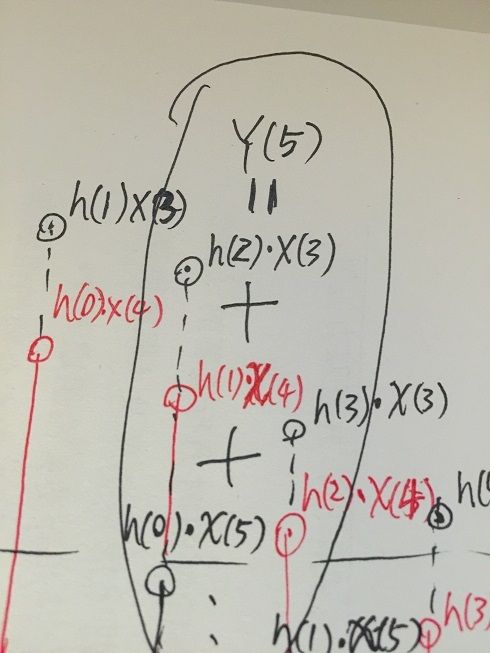
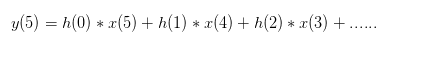
这式子好像在哪里见过?
TM原来卷积的式子是这么回事!!!!!! TM怪不得冲击响应跟原信号一卷儿就对了!!!!
这基本大概就是脉冲响应,卷积,线性时不变系统之间的关系了.
注: 连续脉冲响应,道理上和离散的差不多,拿连续脉冲讲的话一是图不好画,二是比较要命的连续脉冲响应还不是个正常函数,所以使用离散来讲了.
所谓线性时不变系统,首先要线性,然后要时不变:
所谓 线性,指的是如果任意输入x输入系统得到y, 那么x*k输入系统,应该得到y*k,
比如,"乘100"就是个线性系统,因为例如以5为输入得到输出500,而5*6为输入得到
3000 == 5*100*6. 而"平方"则不是线性系统,因为以5为输入得到25,而5*6得到的结果是
30*30 != 5*5*6.
线性时不变系统的另一个特性就是 叠加性, 即假如x进入系统得到结果f(x), 那么若x=a+b,
必有f(x) = f(a) + f(b).
还有就是 时不变,时不变指的是若一个输入x得到信号y,那么一个经过了延迟的x得到的
也只是一个被延迟过的y.而不能是其他值.
举个不太恰当的例子,假设有一个火车站, 今天你去买票买到了今天的票, 明天你去买到了明天的票,那么这个火车站就是个时不变系统,假如今天你去买票买到了今天的票,明天你去买到了大后天的票,那么这个火车站就不是时不变系统.
说了半天了,进入正题,脉冲信号有啥用?
注: 为了方便理解,以下全部使用离散信号:
假设我们有个连续信号,我们不妨对它进行采样,为了方便讲解我把采样率弄低了一点:
可以看到,采样之后得到了一个比较"方块"的波形. 那么, 我们把这个离散化的波形切成6份:
好了,我们得到了6个波形,那么我们会发现这6个波形是大小不一的,我们将其转换为大小
一致的,归一化的6个波形分别乘以不同的系数:
好,那么我们又发现,这六个波形现在大小一样了,只不过互相之间有一些延迟,不要紧,我们把延迟
用系数代替:
发现什么没? 最开始的波形实际上就是6个不同振幅系数,不同延迟系数的脉冲波的线性组合.
但是,即使这样也不能证明脉冲就有用了, 就算波形能被分解成不同振幅系数,不同延迟系数的线性组合, 那又怎么样呢?
回忆一下我们最开始所说的线性时不变系统的定义, 就会发现, 一个信号x(t)输入系统,得到输出y(t),那么k*x(t)输入系统就会得到k*y(t), x(t-T)输入系统就会得到y(t-T),那么,假如我们把刚才的六个信号输入线性时不变系统,就会得到以下内容:
实际上,我们根本不需要让这六个信号都输入系统,由于线性时不变,我们只需要让这六个信号中的任意一个信号归一化,对齐到0时刻,进入系统,再对输出乘以不同系数,延迟不同时间,就得到了所有的输出.
故事到这里还没结束, 还记得咱们这六个信号怎么来的吗? 没错, 是从一个波形上切下来的;
然后,由于线性系统的 叠加性,这个波形的输出就等于那六个信号的输出之和. 而那六个信号又
等于不同延迟,不同系数的脉冲信号, 因此我只需将脉冲信号输入系统,就可以得到完整波形输入
系统后能得到的全部内容---- 无非就是一堆不同延迟,不同系数的脉冲信号的输出之和:
因此对于线性时不变系统来说, 只需要拿脉冲信号"bi"一下,别的什么都不需要研究,就能得到这个线性时不变系统的全部信息了.
//------------------------- 更新 ------------------------------------
再来我们看看卷积:
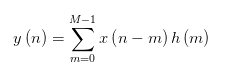
我们知道拿着脉冲对着线性时不变系统H "哔"一下,得到的结果h(t),即冲击响应. 再用这个冲击响应和信号x做卷积,得到的结果y就是x经过线性时不变系统H的结果. 那么问题来了:
1. TM凭什么!
2. 卷积为啥定义成这个德行???
我是从泛函那边儿学过来的,刚看卷积时简直匪夷所思,为啥x和h要反着乘???
跟内积定义的一样不行吗? 其实弄明白上文中脉冲的作用,就不难理解卷积的形式了:
上文中我们知道,只要知道了脉冲经过线性时不变系统的输出结果,就可以用这个输出结果附上系数,延迟,累加出任意信号x的输出y.那么这个累加的过程,如图:
(示意图,明白意思就行了....)
(示意图,明白意思就行了....)
图是好画,可是转换成数学形式就有点麻烦了,为了更规范和精确一点,我们不再使用大方块代表脉冲波,而是使用一根棍儿来代表脉冲波:
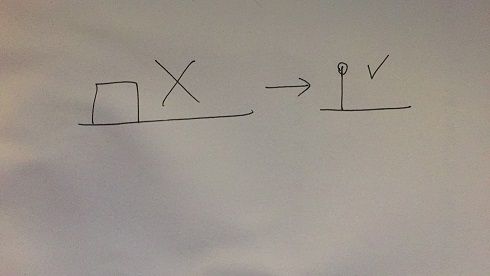
那么,这根棍儿经过了一个线性系统H,得到输出h:
其中,h(0)到h(4)代表着这个h在离散横轴0,1,2,3,4点上的值.
还拿本答案最开始的那个波形举例,只不过将大方块换成棍子:
根据前文,我们已经知道这个x的输出结果无非就是一堆乘以系数,延迟过的h之和,现在要求出x所对应的输出y.先不看前面的,只考虑y(5)的位置,这个位置的值等于多少呢?
首先,将脉冲响应h延迟到y(5)的位置上:
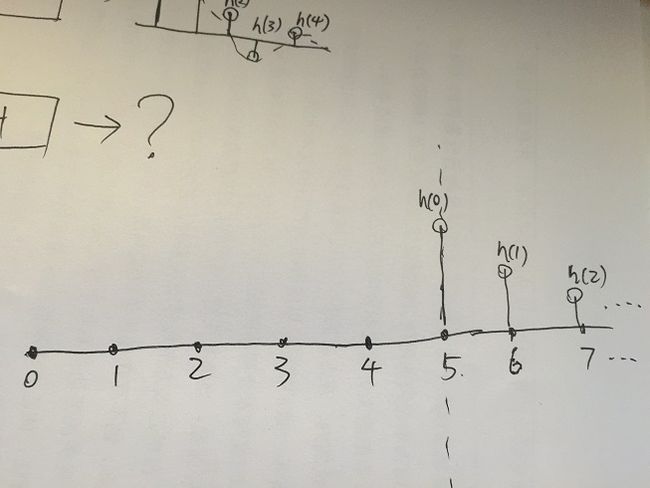
可以看到y(5)上的h已经落座了,但是不要慌,我们光延迟了h,还没乘系数呢, 那么在y(5)的位置上h的系数为多少呢? 因为h是标准化的,最大值为1,所以在y(5)的位置上h的系数就是x(5)啊:
好了,y(5)位置的y值就考虑完毕了........吗? 并没有! 因为y(4)的位置上也有一个h! h是有长度的! 所以h会"拖到"y(5)的位置上, 而且y(4)上的h, 其系数就是x(4). 它们要加起来的啊:
然后呢? 还有y(3)上的h呢:
好了,y(2),y(1)上的h我就先不画了,咱们就盯着y(5)看,仔细看:
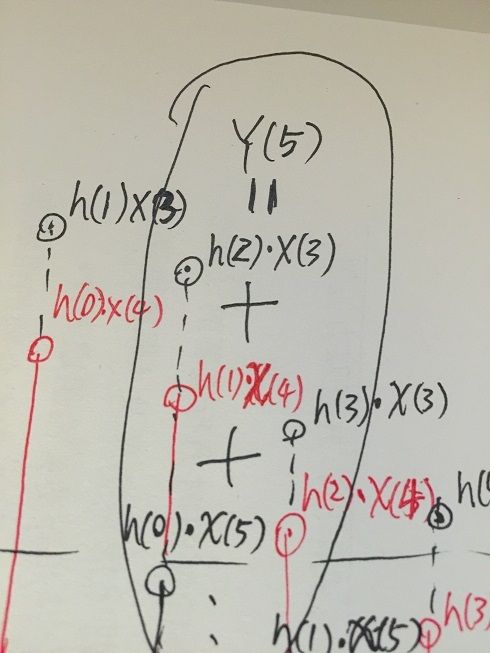
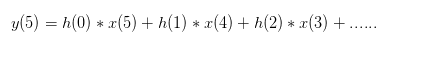
这式子好像在哪里见过?
TM原来卷积的式子是这么回事!!!!!! TM怪不得冲击响应跟原信号一卷儿就对了!!!!
这基本大概就是脉冲响应,卷积,线性时不变系统之间的关系了.
注: 连续脉冲响应,道理上和离散的差不多,拿连续脉冲讲的话一是图不好画,二是比较要命的连续脉冲响应还不是个正常函数,所以使用离散来讲了.