1.《Spectral Networks and Deep Locally Connected Networks on Graphs》论文理解

1.引言

在欧式空间中使用的CNN卷积具有平移不变性，权值共享，局部连接，分层次表达的特点；但是图网络是一种非欧式结构的数据，网络是不规整的关系型数据，所以其不存在平移不变形（每个节点的周围邻居数不固定），导致图网络无法使用传统的CNN。不使用卷积核卷积的话，只能按照全连接网络的方式进行线性映射，这样又将失去权值共享，局部连接，分层次表达这些优势，需要大量的参数。在《Spectral Networks and Deep Locally Connected Networks on Graphs》 中，作者想办法把传统欧式空间的卷积迁移到图网络中去，作者提出了两个结构，把欧式空间的卷积迁移到了图网络的空间域和频域。

2.空间结构

无向图：$G=(\Omega ,W)$，其中$\Omega$表示图中所有节点的集合，size = m；$W$表示图的邻接矩阵，shape = （m,m）,由于是无向图，$W$是一个对称矩阵。$W$中的值$W_{i,j}$表示节点i，j之间的边的权重，为非负值，当这两个节点之间没有边的时候，认为权重值为0。

2.1 节点的邻域

在传统的欧式空间中（以图像为例），在卷积时需要设置一定大小的卷积核，如 kernel = (3,3)，就是相当于中心像素点的邻域为周围的8个像素点。
在图中，利用$W$来确定每个节点的邻域。论文中给出公式：
$$N_{\delta }(j)=\{i\in \Omega :W_{i,j}>\delta \}\text{\hspace{1em}(1)}$$

$N_{\delta }(j)$表示$j$的邻域，是一个集合；以$\delta$为阈值划分节点$j$的邻域，权值大于$\delta$才属于$j$的邻域。

2.3 深度局部连接网络

2.2节中作者在介绍一个传统卷积的分层次表达的特点，这里就不再解释，直接进入2.3节。
在传统的欧式空间中（以图像为例），在卷积时需要设置一定大小的步长，如stride = (3,3)，假设input_image.shape = (18,18),kernel = (3,3)，out_image.shape = (6,6),这个操作相当于在18×18个像素点中找到了6×6个聚类中心，将其进行聚类操作，每个类中的元素为中心点的邻域元素。将每个类与卷积核对应项相乘求和，得到输出的一个像素点。
在图中，作者给出了以下（2）（3）两个公式：
$$N_k=\{N_{k,i};i=1...d_{k-1}\}\text{\hspace{1em}(2)}$$

在公式（2）中，k表示第k个尺度，类比传统卷积，意思就是第k层卷积层，${\Omega }_k$表示第k层输入的节点数目，$d_{k-1}$第k-1层中聚类的类数，即${\Omega }_k=d_{k-1}$，${\Omega }_{k+1}=d_k$表示输出的节点数目，$N_{k,i}$表示第i个节点的类，在这个公式中，作者是以每个输入节点为类中心，以节点邻域为类元素，得到了${\Omega }_k=d_{k-1}$个类。
具体如何得到$N_k$如上图所示：（这些公式就没怎么看懂了）

$$x_{k+1,j}=L_{k}h(\sum _{i=1}^{f_{k-1}}{F}_{k,i,j}{x}_{k,j})（j=1...f_k）\text{\hspace{1em}(3)}$$

在公式（3）中，$f_{k-1}$表示k-1层的滤波器个数，也是k层中每个节点的特征维数。$x_k=(x_{k,i};i=1...f_{k-1})$,$x_k$.shape = ($d_{k-1},f_{k-1}$),表示输入数据；$x_{k,i}$.shape = ($d_{k-1}$,1),表示$d_{k-1}$个节点的第i个特征拼接形成的向量。$F_{k,i,j}$.shape = ($d_{k-1},d_{k-1}$)，表示第k层第j个滤波器的i个值，$F_{k,i,j}$的值与$N_k$有关，表示第k层第j个滤波器的i个特征的映射关系，x节点和y节点不是邻域关系则对应的$F_{k,i,j}(x,y)$的值将为0，和$W$类似。
${\sum }_{i=1}^{f_{k-1}}{F}_{k,i,j}{x}_{k,j}$部分完成了卷积的工作(类比传统的卷积的话，可以认为卷积的模式选择了same，stride = 1)，卷积后输出和输入节点数一样，输出$(d_{k-1},1)$的向量，$h(\ast )$为非线性激励函数，$L_k(\ast )$为池化操作，将$(d_{k-1},1)$的向量池化为$(d_k,1)$的向量，即$x_{k+1,j}.shape=(d_k,1)$，然后，如果第k层有$f_k$个滤波器的话，那么第k层的输出为$x_{k+1}=(x_{k+1,i};i=1...f_k)$。

图上的空间域卷积如下图所示：

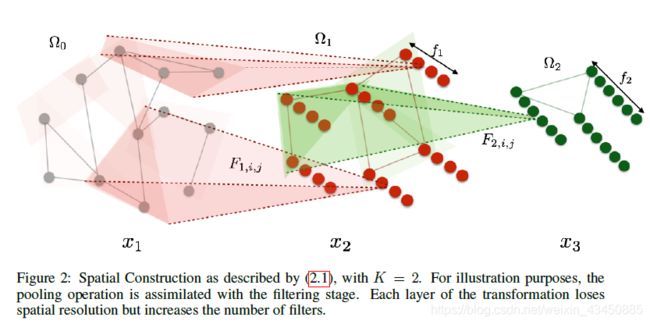
k =1时：
$num({\Omega }_0)=12,x_1.shape=(12,f_0),f_1=4,F_{1,i,j}.shape=(12,12),1\le i\le f_0,1\le j\le f_1,d_1=6$
k =2时：
$num({\Omega }_1)=d_1=6,x_2.shape=(6,f_1),f_2=6,F_{2,i,j}.shape=(6,6),1\le i\le f_1=4,1\le j\le f_2,d_2=3$
网络输出：
$x_3.shape=(d_2,f_2)=(3,6)$

3.频域结构

离散域的卷积公式：$(f\ast g)={\sum }_{\tau =-\infty }^{\infty }f(\tau )g(n-\tau )$
离散傅里叶变换公式（DFT）：$X(k)=F(x(n))={\sum }_{n=0}^{N-1}x(n)e^{-jk\frac{2\pi }{N}n}$ , $k\in [0,N-1]$，表示的是$x(n)$与$\{e^{-jk\frac{2\pi }{N}n}\}$的内积，也可以认为是将$x(n)$映射为$\{e^{-jk\frac{2\pi }{N}n}\}$基向量空间的$X(k)$。
离散傅里叶逆变换公式（IDFT）：$x(n)=F^{-1}(X(k))=\frac{1}{N}{\sum }_{k=0}^{N-1}X(k)e^{jk\frac{2\pi }{N}n}$ , $n\in [0,N-1]$。
由于时域卷积等于频域相乘，所以卷积公式的频域表达：
$$(f\ast g)=F^{-1}[F[f]⨀F[g]]\text{\hspace{1em}(4)}$$

$⨀$表示哈达玛乘积，指的是两个矩阵(或向量)的逐点乘积。
在图网络中，定义了度矩阵$D$，$D$为对角矩阵，对角线上的值为各个节点连接的边的数目，$W$为图的邻接矩阵，图中的拉普拉斯矩阵定义为$L=D-W$，对$L$进行矩阵的特征分解，得到：$L=V\Lambda V^T$,$V=(v_1,...,v_i,...v_n),v_i$是$L$的特征向量，$\Lambda =diag({\lambda }_1...{\lambda }_i...{\lambda }_n)$,${\lambda }_i$是$L$的特征值。所以:
$$L{v}_i={\lambda }_i{v}_i\text{\hspace{1em}(5)}$$

而所有的基向量$\{e^{-jk\frac{2\pi }{N}n}\}$都满足亥姆霍兹方程（Helmholtz Equation）：
$${\nabla }^{2}f=\frac{{\partial }^2{e}^{-jk\frac{2\pi }{N}n}}{\partial n^2}=-(k\frac{2\pi }{N}{)}^2{e}^{-jk\frac{2\pi }{N}n}=-w^{2}f\text{\hspace{1em}(6)}$$

${\nabla }^2$是拉普拉斯算子，$e^{-jk\frac{2\pi }{N}n}$是拉普拉斯算子${\nabla }^2$的特征函数,$-w^2$是特征函数的特征值。
将式(5)和式(6)对比，可知：$e^{-jk\frac{2\pi }{N}n}$~$v_i$,$-w^2$ ~ ${\lambda }_i$。
用$f$表示时域信号，$\hat{f}$表示相应的频域信号，将这两个类比带入离散傅里叶变换的公式，得到：
$$\hat{f}(k)=\sum _{n=0}^{N-1}f(n)e^{-jk\frac{2\pi }{N}n}=\sum _{n=0}^{N-1}f(n)v_k(n)=v_k^{T}f\text{\hspace{1em}(7)}$$

由式(7)可知：
$$\hat{f}=V^{T}f\text{\hspace{1em}(8)}$$

将式(8)带入卷积公式得：
$$(g\ast f)=V[V^{T}g⨀V^{T}f]\text{\hspace{1em}(9)}$$

由于$V^{T}g=(v_1^{T}g,...,v_n^{T}g{)}^T$,所以$V^{T}g⨀V^{T}f=diag(v_1^{T}g,...,v_n^{T}g)V^{T}f$,令$g_{\theta }=diag(v_1^{T}g,...,v_n^{T}g)$,所以$$(g\ast f)(n)=V{g}_{\theta }{V}^{T}f\text{\hspace{1em}(10)}$$

论文中所给的频域公式为：
$$x_{k+1,j}=h(V\sum _{i=1}^{f_{k-1}}{F}_{k,i,j}{V}^T{x}_{k,i})\text{\hspace{1em}(11)}$$

在式(11)中$F_{k,i,j}$就是$g_{\theta }$，$x_{k,i}就是f$，$f$相当于输入信号$x$的一个通道的信号。所以在每个通道求完卷积后，将结果累加，得到输出结果的一个通道的值。$x_{k,i}$表示第k层所有节点的第i个特征拼接形成的向量。$F_{k,i,j}$表示第k层第j个滤波器的i个值的频域表示(类比于传统卷积的第$j$个卷积核的第$i$个通道),$h(\ast )$依然是非线性激活函数。

论文其他内容:
(1)经常情况下，V只有前d个特征向量起作用，因此取前d个特征向量，以减少参数。
(2)通过样条差值的方法，近似的求出这个操作的解，而使权值参数减少到O(1)。
(3)实验部分。