《Object Co-segmentation via Graph Optimized-Flexible Manifold Ranking》阅读笔记
1.目标协同分割
给定一组包含同一语义类中相同或相似对象的图像,目标共分割的目的就是从所有图像中发现并分割出这些协同对象示。

2.图像特征
给定一组相关图像集合 Ω = { I 1 , . . . I m } \Omega = \{I_1,...I_m\} Ω={ I1,...Im},利用 S L I C SLIC SLIC聚类算法(参考上篇博客《SLIC Superpixels Compared to State-of-the-Art Superpixel Methods》阅读笔记),将这些图像分割,得到 n = ∑ i = 1 n n i n=\sum_{i=1}^n{n_i} n=∑i=1nni个超像素, n i n_i ni表示第 i i i张图像分割后得到的超像素的数目。
文中作者采用了两种低层外观特征和高层语义特征来捕获每个超像素的不同特征:
(1)低层外观特征
低层外观特征对图像的外观变化非常敏感。低层外观特征可以检测目标具有一致的外观和明确的目标边界。所以作者直接将图像进行超像素分割,并对每个超像素提取了颜色、纹理和 S I F T SIFT SIFT特征作为低层外观特征,分别用 c 1 , c 2 , c 3 c_1,c_2,c_3 c1,c2,c3表示。
(2)高层语义特征
高层语义特征利用ImageNet预训练的CNN-S模型进行特征提取,得到通道数为512的特征图。接着将特征图上采样到原始图像大小,并SLIC算法分割得到超像素,将超像素进行最大池化的得到长度为512的节点特征,最后利用自编码器对长度为512的节点特征进行处理,得到长度为24的节点特征表示,用 c 4 c_4 c4表示。
3.图结构
通过前面对低层外观特征、高层语义特征的处理可以得到图数据中的节点特征,每个超像素对应于图中的一个节点。
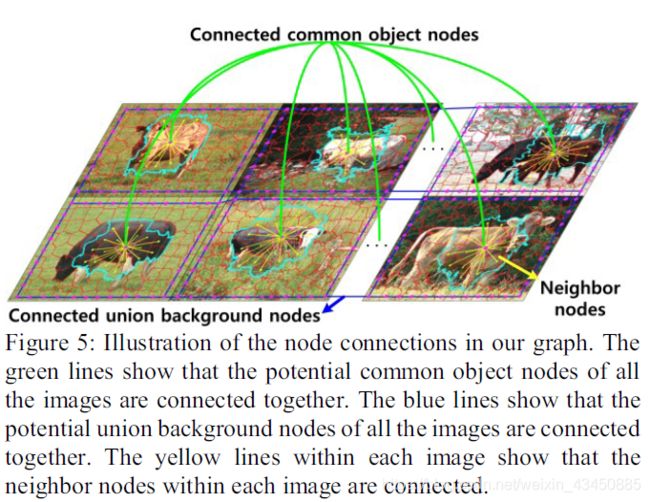
由于在空间上具有相似特征的相邻节点往往属于同一类,因此作者将相邻的超像素对应的节点相连,从而对每张图像中的图像内约束进行建模。(图中黄线)
背景的先验知识来自于摄影构图的基本规则,作者认为大多数摄影师不会沿着取景框裁剪感兴趣的对象。换句话说,图像的边界主要是背景。基于此先验,作者在第一阶段通过连接整个图像组边界上的超像素节点,作为联合背景。(图中蓝线)
作者希望得到这样的图结构信息,所以构建节点的邻接矩阵:
a i j = e x p ( − ∑ t = 1 3 ( λ t ∣ ∣ c t i − c t j ∣ ∣ 2 ) ) (1) a_{ij}=exp(-\sum_{t=1}^3(\lambda_t{||c_t^i-c_t^j||}^2))\tag1 aij=exp(−t=1∑3(λt∣∣cti−ctj∣∣2))(1)
a i j = e x p ( ∣ ∣ c 4 i − c 4 j ∣ ∣ 2 ) (2) a_{ij}=exp({||c_4^i-c_4^j||}^2)\tag2 aij=exp(∣∣c4i−c4j∣∣2)(2)
协同目标相似,所以所有于目标有关的节点之间的边权重较大,背景与目标不相似,边的权值比较小。 通过 L = D − A L=D-A L=D−A得到图的拉普拉斯矩阵。
4.GO-FMR算法
S S S表示最佳邻接矩阵,作者认为设计的邻接矩阵不一定是最佳的邻接矩阵,但是含有大量的结构信息,所以作者不希望 S S S与 A A A之间变化过大,所以加入了 η ∣ ∣ S − A ∣ ∣ F 2 \eta{||S-A||}^2_F η∣∣S−A∣∣F2项。 w w w和 b b b分别为图卷积的映射矩阵和偏置。 f = [ f 1 , . . . f n ] f=[f_1,...f_n] f=[f1,...fn]为预测值, y = [ y 1 , . . . , y n ] y=[y_1,...,y_n] y=[y1,...,yn]是标签, y i = 1 y_i=1 yi=1表示对应节点属于一类, y i = 0 y_i=0 yi=0表示对应节点没有标签。 U U U为对角矩阵,当节点i有标签时, u i i = 1 u_{ii}=1 uii=1,没有标签 u i i = 0.001 u_{ii}=0.001 uii=0.001。
定义损失函数:
L o s s = t r ( f − y ) T U ( f − y ) + μ ∣ ∣ X T w + b − f ∣ ∣ 2 2 + t r ( f T L s f ) T + η ∣ ∣ S − A ∣ ∣ F 2 (3) Loss=tr{(f-y)}^TU(f-y)+\mu{||X^Tw+b-f||}^2_2+tr{(f^TL_sf)}^T+\eta{||S-A||}^2_F\tag3 Loss=tr(f−y)TU(f−y)+μ∣∣XTw+b−f∣∣22+tr(fTLsf)T+η∣∣S−A∣∣F2(3)
优化参数为: f , w , b , S f,w,b,S f,w,b,S。公式的第一项保证 f f f接近已标记节点的给定标签,第二项保准映射值和预测值差距尽可能小,第三项保证 f f f对于整个图中没有标记的和有标记的节点来说是光滑的,第四项保证 S S S与 A A A之间变化不会过大。
迭代交替优化参数:
(1)固定 S S S,优化 f , w , b f,w,b f,w,b,保证损失最小,通过FME算法,可以得到他们的最优解:
f = ( U + L s + μ H c + μ N ) − 1 U y w = ( X c X T ) − 1 X c f b = 1 n ( f T 1 → − w T X 1 → ) (5) \begin{aligned} &f=(U+L_s+\mu H_c+\mu N)^{-1}Uy\\ &w=(X_cX^T)^{-1}X_cf\\ &b=\frac{1}{n}(f^T \overrightarrow1 -w^TX \overrightarrow1) \end{aligned}\tag5 f=(U+Ls+μHc+μN)−1Uyw=(XcXT)−1Xcfb=n1(fT1−wTX1)(5)
其中, N = ( X c T ( X c X T ) − 1 X c [ X T ( X c X T ) − 1 X c − 2 I ] ) , X c = X H c , H c = I − ( 1 / n ) 1 → 1 → T N=(X_c^T(X_cX^T)^{-1}X_c[X^T(X_cX^T)^{-1}X_c-2I]),X_c=XH_c,H_c=I-(1/n)\overrightarrow1\overrightarrow1^T N=(XcT(XcXT)−1Xc[XT(XcXT)−1Xc−2I]),Xc=XHc,Hc=I−(1/n)11T, 1 → \overrightarrow1 1表示值全为1的向量。
(2)固定 f , w , b f,w,b f,w,b,计算 S S S, L o s s Loss Loss的前两项为常数,则:
S = a r g m i n S ( t r ( f T L s f ) + η ∣ ∣ S − A ∣ ∣ F 2 ) (8) S=argmin_S(tr{(f^TL_sf)}+\eta{||S-A||}^2_F)\tag8 S=argminS(tr(fTLsf)+η∣∣S−A∣∣F2)(8)
交替进行(1)(2)过程,得到参数为 f , w , b , S f,w,b,S f,w,b,S。
GO-FMR算法训练过程伪代码:

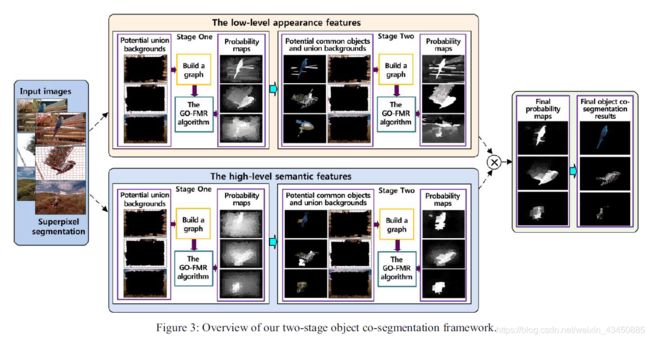
5.协同分割框架
作者首先将联合背景初始化为所有图像边界上的超像素。然后将所有初始化的并集背景节点连接在一起,并将所有空间相邻节点连接在一起,构造一个图。接下来,将所有初始化的并集背景节点作为标签1的标记节点,使用GO-FMR算法计算所有超像素节点预测标签 f ( 1 ) f^{(1)} f(1),协同分割的目标是与联合背景不同的,所以预测值小的地方是目标的概率就大:
I ( 1 ) = ( f ‾ ( 1 ) > = β ∗ m e a n ( f ‾ ( 1 ) ) ) (9) I^{(1)}=( \overline f ^{(1)}>=\beta *mean( \overline f ^{(1)}))\tag9 I(1)=(f(1)>=β∗mean(f(1)))(9)
其中, f ( 1 ) = 1 → − f ( 1 ) f ^{(1)}=\overrightarrow 1-f^{(1)} f(1)=1−f(1)。在得到的概率图 I ( 1 ) = [ l 1 ( 1 ) , . . . , l 1 ( n ) ] I^{(1)}=[l_1^{(1)},...,l_1^{(n)}] I(1)=[l1(1),...,l1(n)]中,值为1表示目标,0为背景。
将 I ( 1 ) = [ l 1 ( 1 ) , . . . , l 1 ( n ) ] I^{(1)}=[l_1^{(1)},...,l_1^{(n)}] I(1)=[l1(1),...,l1(n)]输入第二阶段中,以此为目标先验,按照同样的方法构建图,利用GO-FMR算法得到协同目标的概率图,值在[0,1]中。只有被低层和高层特征共同标记的像素才是目标,所以将低层和高层特征得到的最后的概率图逐点相乘,得到最后的概率图,并利用Grab-cut算法将其映射为二值的分割图,得到最后的分割图像。